|
|
HŘÍŠNÍCI NOVÝ UŽIVATEL nepřihlášený uživatel Právě si tyto stránky čte 1 člověk. |
|
Poslední změna:
29.09.2007 |
|
Návštěvník číslo: 26421 |
| ICQ:61783389 |
|
Copyright © 2003 Hell |
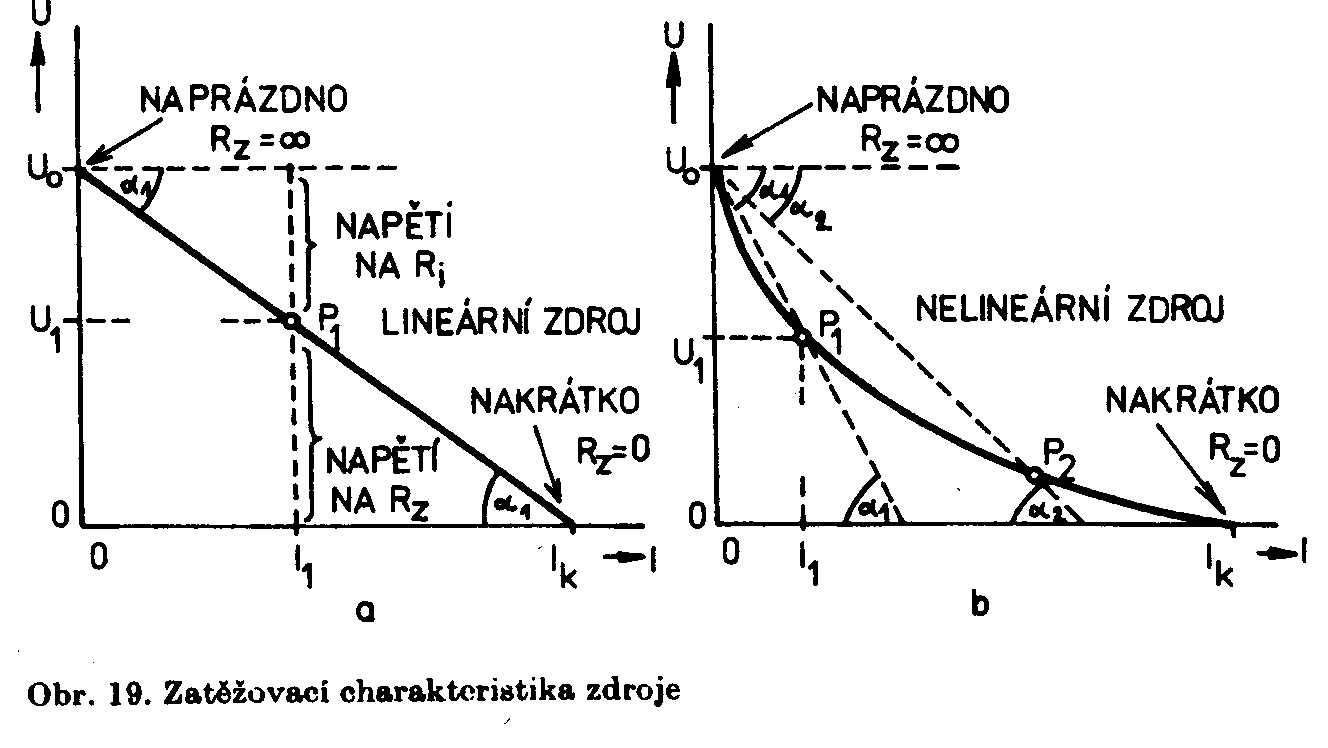
ElektronikaMaturitní otázkyMETODY ŘEŠENÍ ELEKTRICKÝCH OBVODŮ1.METODY ŘEŠENÍ ELEKTRICKÝCH OBVODŮ 1. Skutečný a ideální zdroj elektrické energie a) Charakteristické veličiny zdroje elektrické energie Elektrická energie je dodávána do obvodu napětím U a proudem I. Závislost těchto dvou veličin ( při odebírání proudu ) je zatěžovací charakteristika zdroje. Ri…vnitřní odpor zdroje; Rz…odpor zátěže Vnitřní odpor lineárního zdroje je na velikosti odebíraného proudu nezávislý. Vnitřní odpor nelineárního zdroje je na velikosti odebíraného proudu závislý. Kolísá-li při činnosti zdroje odebíraný proud,
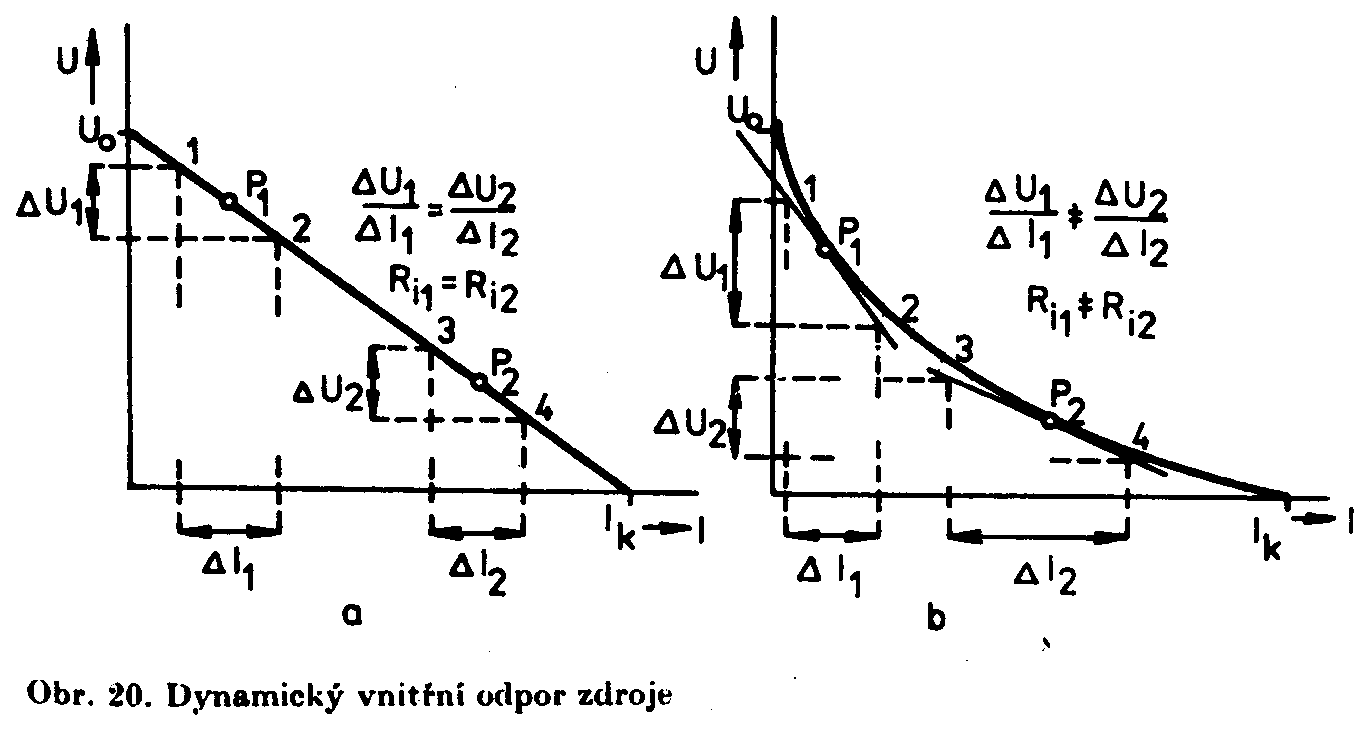
dochází k odpovídajícím kolísání výstupního napětí. Uplatňuje se dynamický
vnitřní odpor zdroje ri, který určujeme pomocí tečny sestrojené k zatěžovací
charakteristice v klidovém bodě. Dynamický Ri lin. zdroje se rovná statickému Ri. Dynamický Ri nelin. zdroje se liší v závislosti na poloze tečny v místě prac. bodu. b) Charakter zdroje Zatěžovací charak. elektrické energie, který udržuje
na svých výstupních svorkách konstantní napětí bez ohledu na velikost odebíraného
proudu, prochází bodem U0 rovnoběžně s vodorovnou osou. Při
zvětšování zatěžovacího proudu nevzniká na vnitřním odporu zdroje žádný úbytek
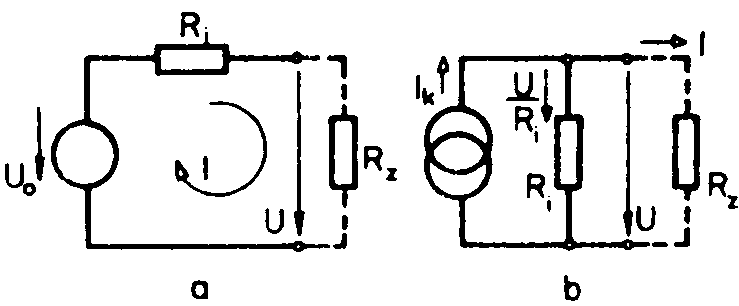
napětíèRi = 0; Zatěžovací charak. elektrické energie, jehož svorkami by procházel proud stále hodnoty Ik bez ohledu na velikost odporu zatěž. rezistoru, by procházel bodem Ik rovnoběžně se svislou osou. Jakékoliv konečné změně svorkového napětí by odpovídala nulová změna proudu. Ri à ¥; U0 = Ri.Ik není definován ( U0 à ¥ ). Takový zdroj nazýváme ideální zdroj proudu. Skutečný zdroj elektrické energie nemá zatěžovací charakteristiku rovnoběžnou ani s osou proudu ani s napětí. Jeho náhradní si můžeme představit jako sériové zapojení ideálního zdroje napětí a vnitřního odporu. Stejnou zatěžovací charakteristiku získáme také při paralelním zapojení Ri k ideálnímu zdroji proudu. Skutečné zdroje ele. energie, které se svými vlastnostmi blíží ideálnímu zdroji napětí, mají ve srovnání s odporem Rz malý Ri, nazýváme je zdroje napěťově tvrdé. Naopak zdroje ele. energie, které se svými vlastnostmi blíží ideálnímu zdroji proudu, nazýváme zdroje napěťově měkké. c) Přenos výkonu ze zdroje do zátěže Činný výkon přenášený ze zdroje s napětím U0 a s vnitřním odporem Ri do zátěže, která má odpor Rz, můžeme určit ze vztahu : P = Rz.I2 Proud I procházející obvodem vypočteme dle ohmova zákona
: Po dosazení do předcházejícího vztahu dostaneme :
Vydělením čitatele i jmenovatele Ri2
získáme vztah : Ze kterého je zřejmé, že výkon odevzdávaný zátěží závisí na poměru zatěžovacího odporu a vnitřního odporu zdroje. Napětí na prázdno U0 a proud na krátko Ik jsou charakteristické veličiny zdroje. Jejich součin se rovná výkonu vnitřního zdroje elektromotorického napětí U0 při nulovém zatěžovacím odporu Rz; tj. při zkratovaných výstupních svorkách. Za této situace je výstupní nap. U nulové, užitečný výkon dodávaný zdrojem do zátěže je roven 0 a veškerý výkon zdroje vnitřního elektromotorického napětí se ve vnitřním odporu Ri mění na teplo. Zvětšujeme-li zatěžovací odpor, zmenšuje se procházející
proud a klesá celkový výkon zdroje. Závislost celkového výkonu zdroje na poměru
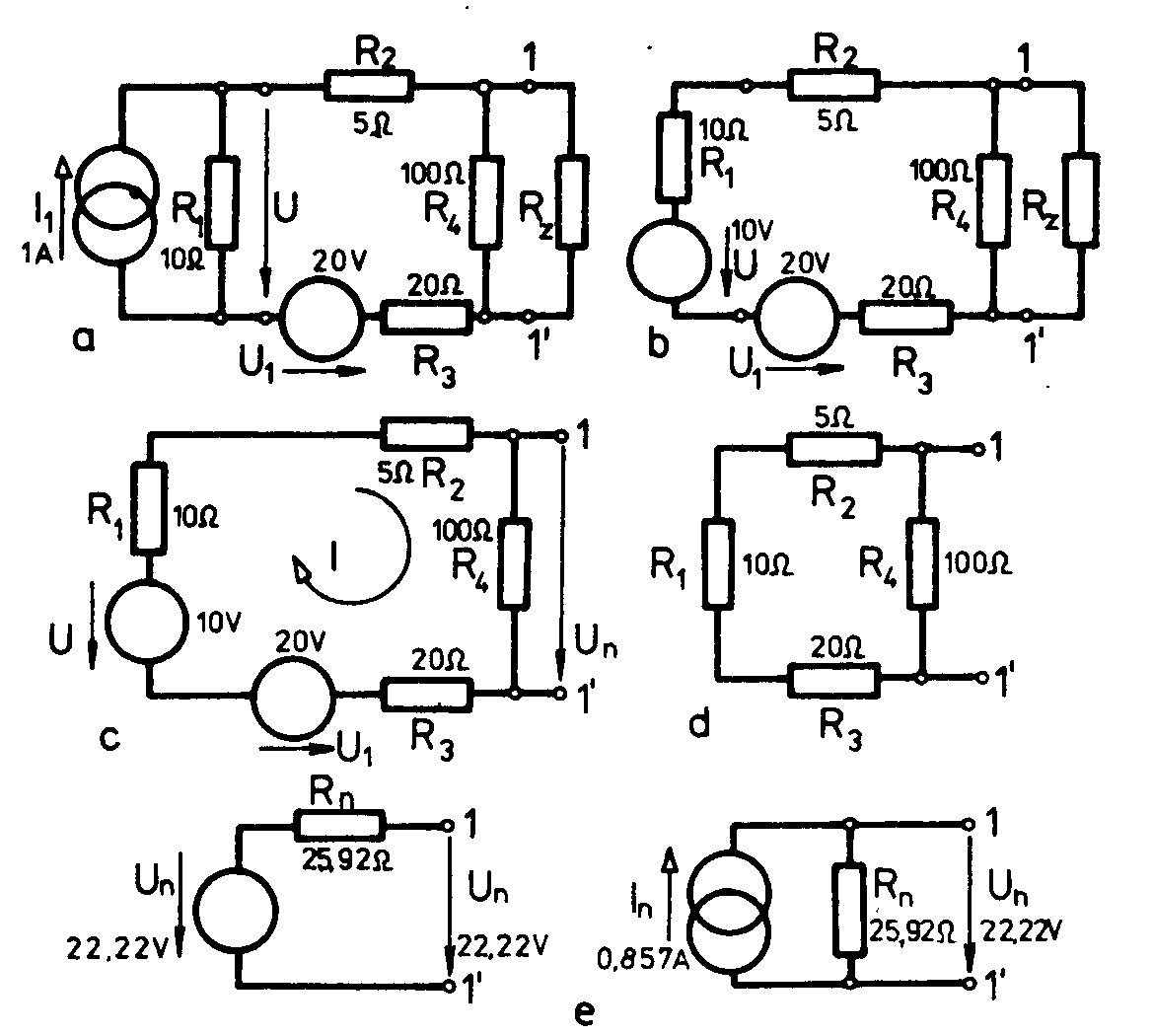
2. Řešení lineárních obvodů a) věty o náhradním obvodu lineár. zdroje Théveninova věta říká, že jakýkoliv aktivní lineární jednobran je možné nahradit sériovým zapojením ideálního zdroje napětí Un a odporem Rn. Přičemž Un je napětí naprázdno na svorkách původního zdroje a Rn je jeho vnitřní odpor. Podle Nortonovy věty lze jakýkoliv aktivní jednobran nahradit ideálním zdrojem proudu In zapojením paralelně k vnitřnímu odporu původního jednobranu. Náhradní proud In se rovná proudu, který prochází svorkami původního jednobranu při jejich spojení nakrátko. Při výpočtu náhradního odporu Rn nahradíme všechny zdroje elektrické energie obsažené ve zjednodušované části jejich vlastními Rià Ideální zdroj napětí : Ri = 0 – skrat, Ideální zdroje proudu : Ri = ¥ - rozpojení. Př. : Část obvodu nalevo od svorek 1,1‘ máme nahradit
podle Theneninovy a Nortonovy věty. Nejprve nahradíme ideální zdroj proudu I1
s pralelně zapojeným R1 sériovým zapojení zdroje U a vnitřního
odporu Ri=R1. U = R1.I1 = 10.1 =
10V. Získáme obvod b). Náhradní napětí Un vznikne podle Then. věty
na rezistoru R4 po odpojení zatěž. odporu Rz. c)
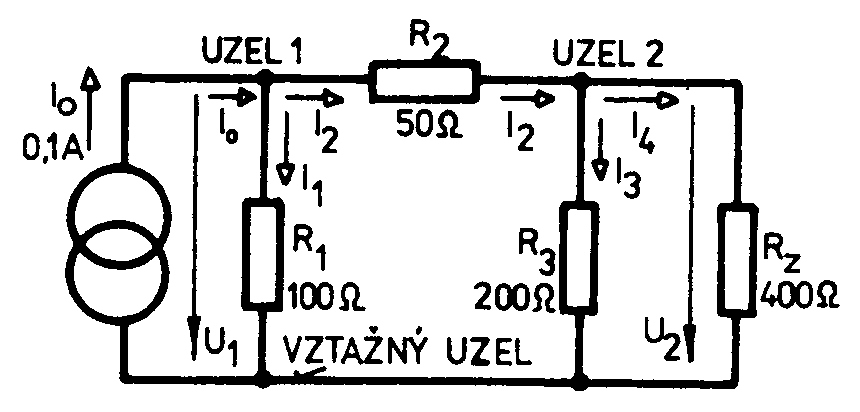
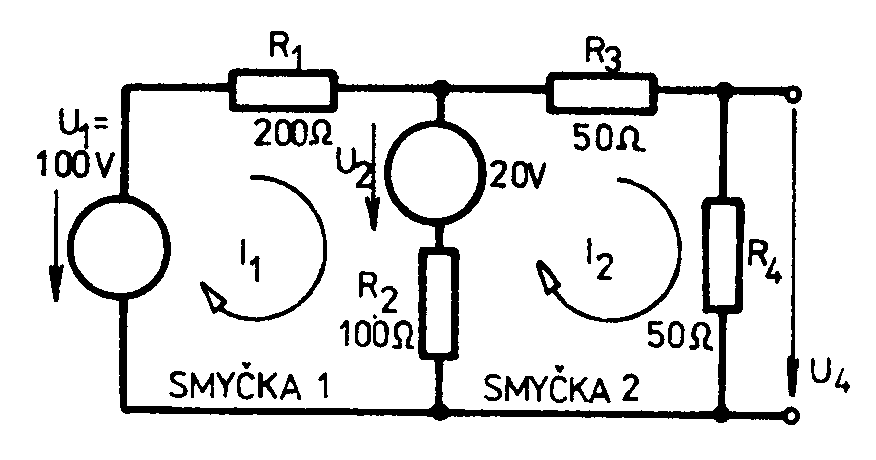
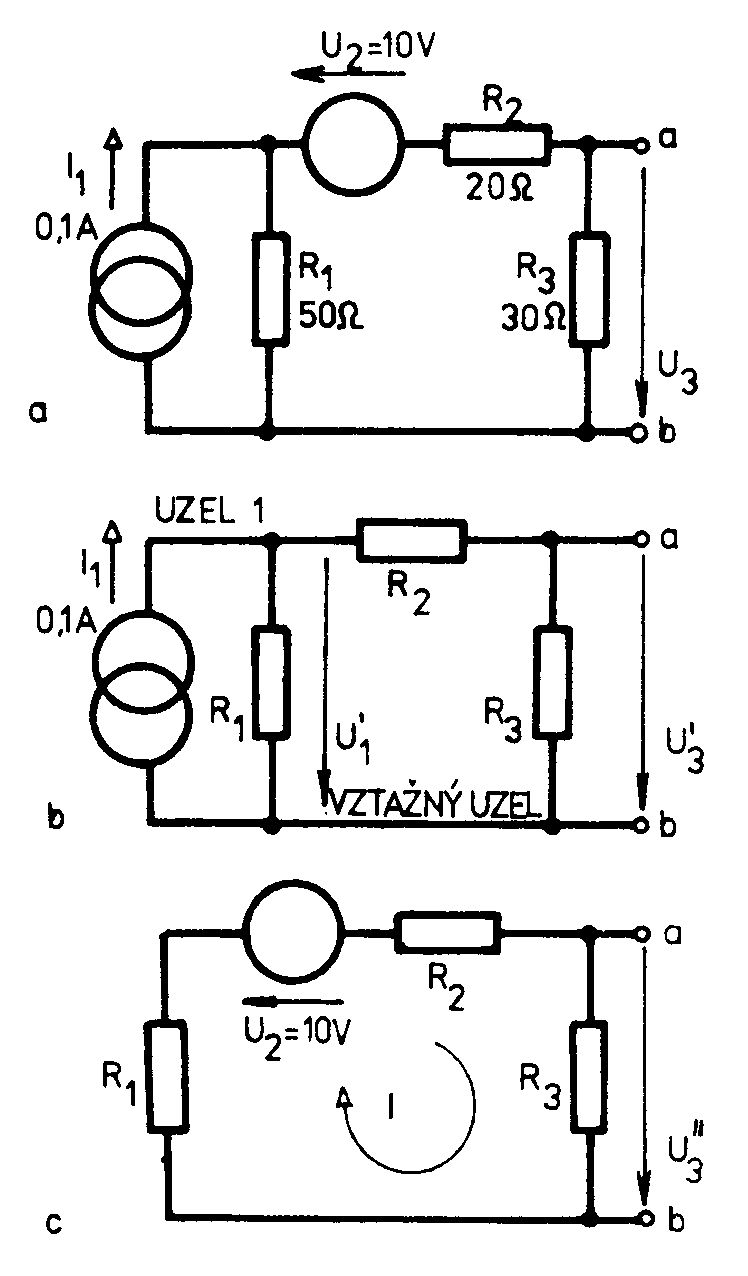
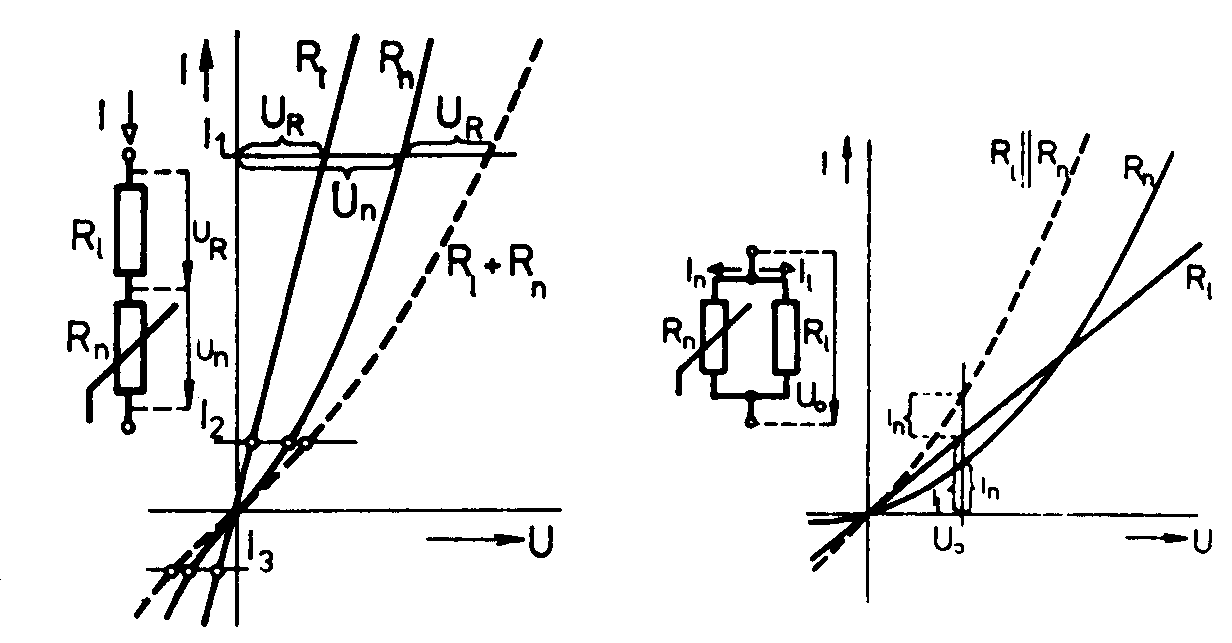
b) využití kichhoffových zákonů pro řešení lin. Obvodu Metoda uzlových napětí : máme vyřešit obvod uvedený níže. Za vztažný uzel zvolíme uzel společný součástkám R1,R3 a Rz, zbývající dva uzly označíme 1 a 2. Sestavíme rovnice : Uzel 1…I0 = I1 + I2… Uzel 2…I2 = I3 + I4… Řešením dostaneme U1=6,47V a U2=4,7V Metoda smyčkovývh proudů : Hledáme např. napětí U4 v obvodu uvedeném níže. Zvolíme a označíme proudy ve smyčkách a sestavíme rovnice : Pro smyčku 1 … 0 = R1I1+U2+ R2(I1- I2)-U1 Pro smyčku 2 … 0 = R3I2+ R4I2+ R2(I2- I1)-U2 Řešením těchto rovnic získáme I1 = 0,36A a I2 = 0,28A. Hledané napětí U4 = R4.I2 = 50.0,28 = 14V vyšlo kladné. Znamená to, že jeho skutečná polarita souhlasí s vyznačeným směrem. c) princip lineární superpozice Pro usnadnění řešení obvodů s několika zdroji elektrické energie je výhodné využít principu lineární superpozice, který platí v lineárních obvodech. Dle tohoto principu řešíme daný obvod postupně vždy s jedním zdrojem. Přitom ostatní zdroje nahradíme jejich vnitřním odporem. Výsledné napětí působící mezi libovolnými místy obvodů všech zdrojů určíme jako součet napětí nebo proudů vypočtených při působení jednotlivých zdrojů samostatně. Př.: Využitím principu lineární superpozice máme určit napětí U3
v obvodu. Nejprve vyřadíme zdroj napětí U2 a řešíme obvod pouze
se zdrojem proudu I1. Získaný obvod b) vyřešíme metodou uzlových
napětí. Obvod má totiž dvě smyčky a dva uzly, z nichž jeden zvolíme jako
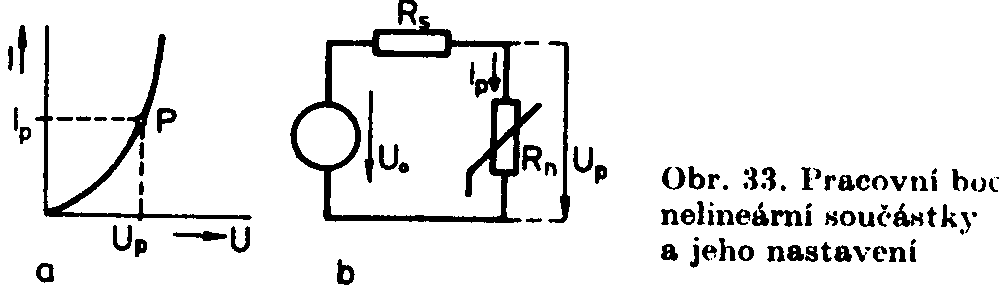
vztažný. Výsledné napětí při současném působení obou zdrojů : U3 = U3‘ + U3‘‘ = 1,5 + 3 = 4,5V. 3. Řešení nelineárních obvodů sériové řazení odporů – paralelní řazení odporů 4.Grafické určení pracovního bodu nelineární součástkyPracovní bod je bodem voltampérové charakteristiky, který odpovídá skutečným pracovním podmínkám součástky v obvodu. Znamená to, že volbou pracovního bodu na voltampérové charakteristice volíme i podmínky činnosti součástky. Je tedy zřejmé, že při návrhu obvodu je velmi důležité, aby byla správně zvolena a nastavena poloha pracovního bodu. Souřadnice zvoleného pracovního bodu UP a IP udávají svorkové napětí součástky a procházející proud. Obě hodnoty jsou stejnosměrné. Odpovídajícímu pracovnímu bodu říkáme statický klidový pracovní bod. Nastavit jeho polohu znamená přivést do součástky odpovídající hodnoty obvodových veličin z napájecího zdroje. Velikost proudu omezujeme podle potřeby sériovým rezistorem RS. |
|
zpět na předchozí stránku
Copyright © 2003 Hell
doporučené rozlišení 1024x768

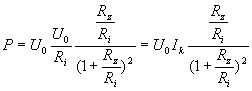
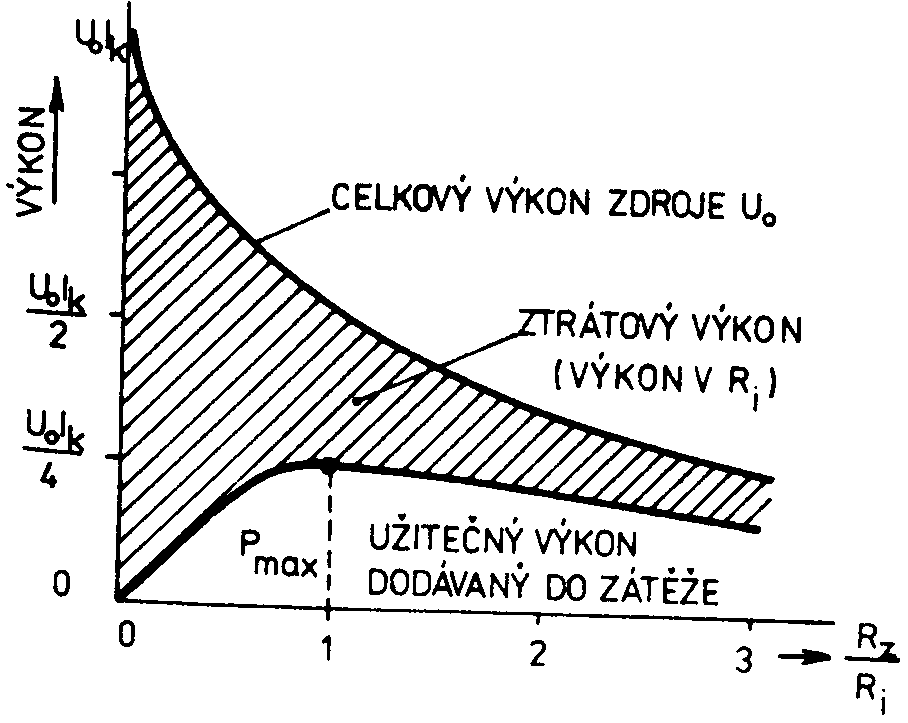
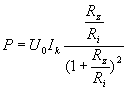 . Dosadíme-li
do tohoto vztahu jednotlivé hodnoty podílu
. Dosadíme-li
do tohoto vztahu jednotlivé hodnoty podílu