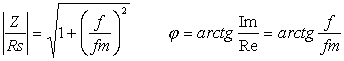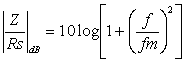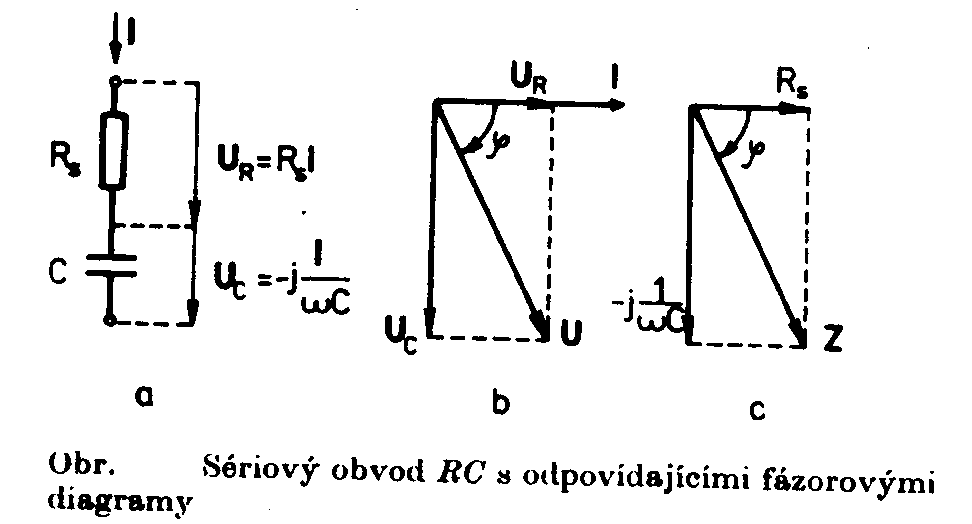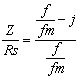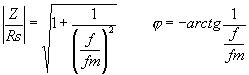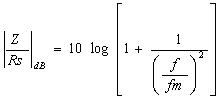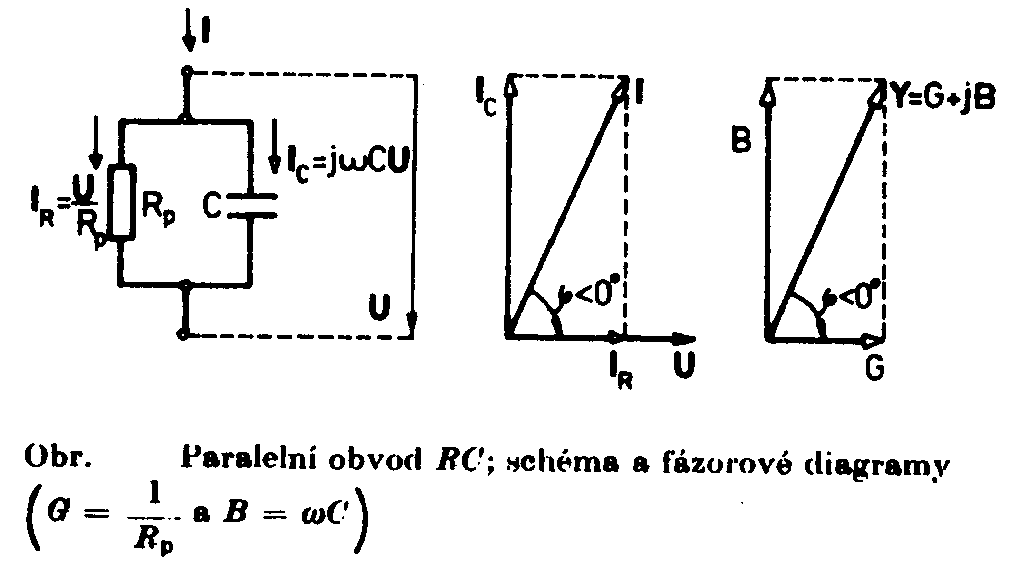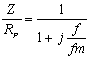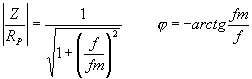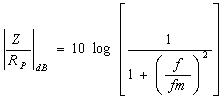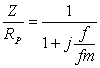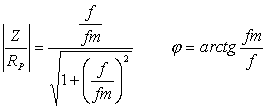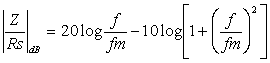|
|
HŘÍŠNÍCI NOVÝ UŽIVATEL nepřihlášený uživatel Právě si tyto stránky čte 1 člověk. |
|
Poslední změna:
29.09.2007 |
|
Návštěvník číslo: 26421 |
| ICQ:61783389 |
|
Copyright © 2003 Hell |
ElektronikaMaturitní otázkyKOMPLEXNÍ JEDNOBRANY – IMPEDANČNÍ VLASTNOSTI15.Komplexní jednobrany – impedanční vlastnostiLineární komplexní jednobrany jsou složeny z lineárních rezistorů, bezeztrátových cívek a kondenzátorů. (Ztrátové odpory skutečných cívek a kondenzátorů jsou připojeny k činným odporům). V této otázce budeme zjišťovat průběhy pouze pro harmonický průběh obvodových veličin. Ačkoliv je možné psát pro lineární jednobrany charakteristické rovnice, určující vztah mezi proudem a napětím, i kreslit voltampérové charakteristiky (přímky procházející počátkem se sklonem závislým na frekvenci), je v praxi důležitější znát impedanci těchto obvodů a její frekvenční závislost. Impedance komplexního jednobranu je vyjádřena komplexním číslem závislým na frekvenci, které můžeme zapsat dvěma rovnocennými způsoby – ve složkovém nebo exponenciálním tvaru. Z = R + jX = Zejj kde |Z| = j
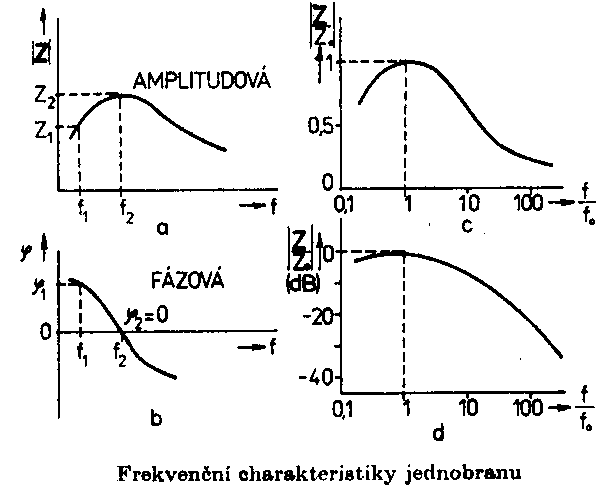
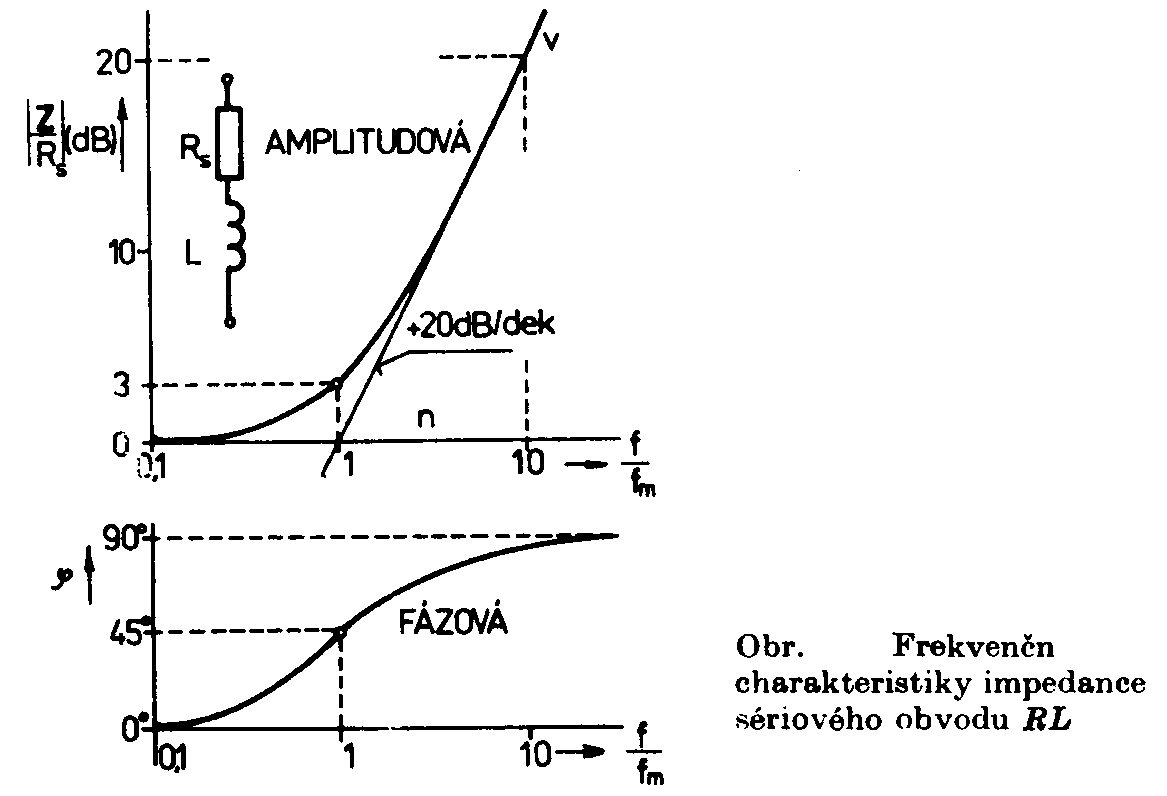
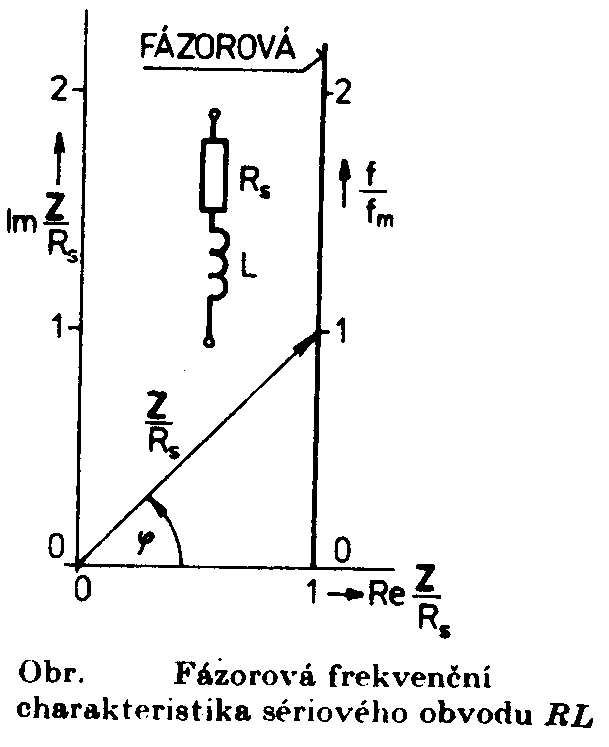
= arctg R = |Z| cos j - činný odpor jednobranu X = |Z| sin j - reaktance jednobranu Obraz impedance Z v komplexní rovině a vzájemný vztah mezi veličinami Z,|Z|,R,X a j je pro jednu frekvenci zobrazen na následujícím obrázku. Pro jinou frekvenci má obecně fázor Z jinou polohu, neboť jeho složky jsou závislé na frekvenci. Závislosti impedance jednobranu na frekvenci vyjadřujeme často graficky formou záznamu absolutní hodnoty a fáze ve dvou samostatných frekvenčních charakteristikách. Ve frekvenční charakteristice absolutní hodnoty impedance (amplitudové charakteristice) |Z| = Z(f ) a ve fázové frekvenční charakteristice |Z|=Z(f). Vodorovné osy, na které vynášíme frekvenci, mívají nejčastěji logaritmickou stupnici, neboť zpravidla musí obsáhnout rozsáhlé frekvenční pásmo. Svislá osa, na kterou vynášíme impedanci, je rovněž dělena logaritmicky. Častěji se používá stupnice lineární, avšak impedance se vynáší v decibelech (logaritmických jednotkách). Přepočet na decibely se provádí podle vztahu ZdB = 20 log |Z|. Použitím obou způsobů dostáváme stejný tvar průběhu charakteristiky. Vyjádření v decibelech je však častější. Fázové úhly se vynášejí v lineárním měřítku na svislé ose. V mnoha případech je výhodné zvolit některou frekvenci
za vztažnou a ostatní frekvence vyjadřovat poměrem k této frekvenci. Vodorovná
osa je pak bezrozměrná. Podobným způsobem se vyjadřuje též impedance. Za vztažnou
hodnotu byla zvolena impedance Z0 při frekvenci f=f0.I
v těchto případech je obvyklé užívání logaritmických stupnic nebo vyjadřování
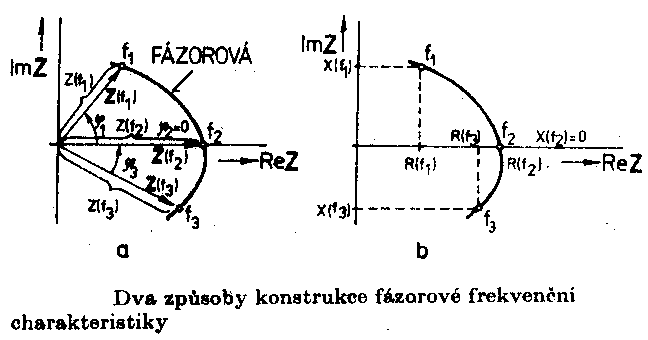
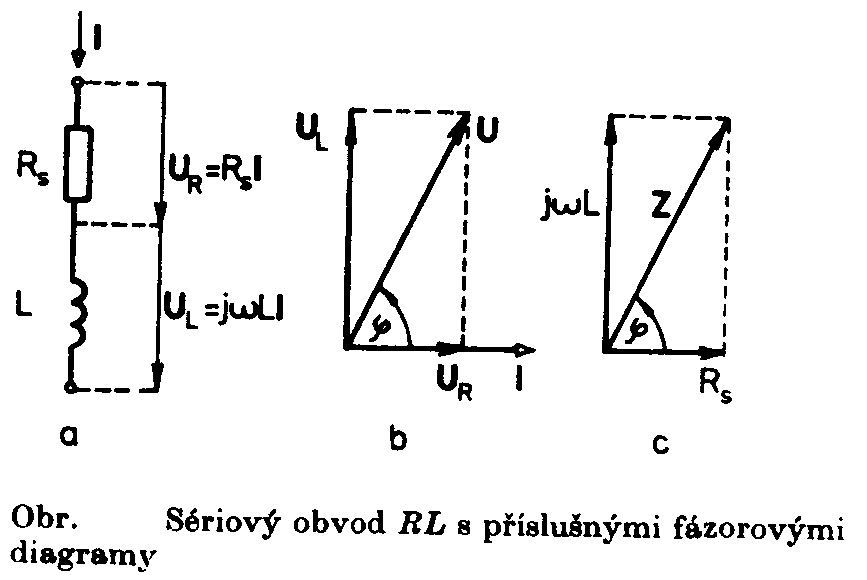
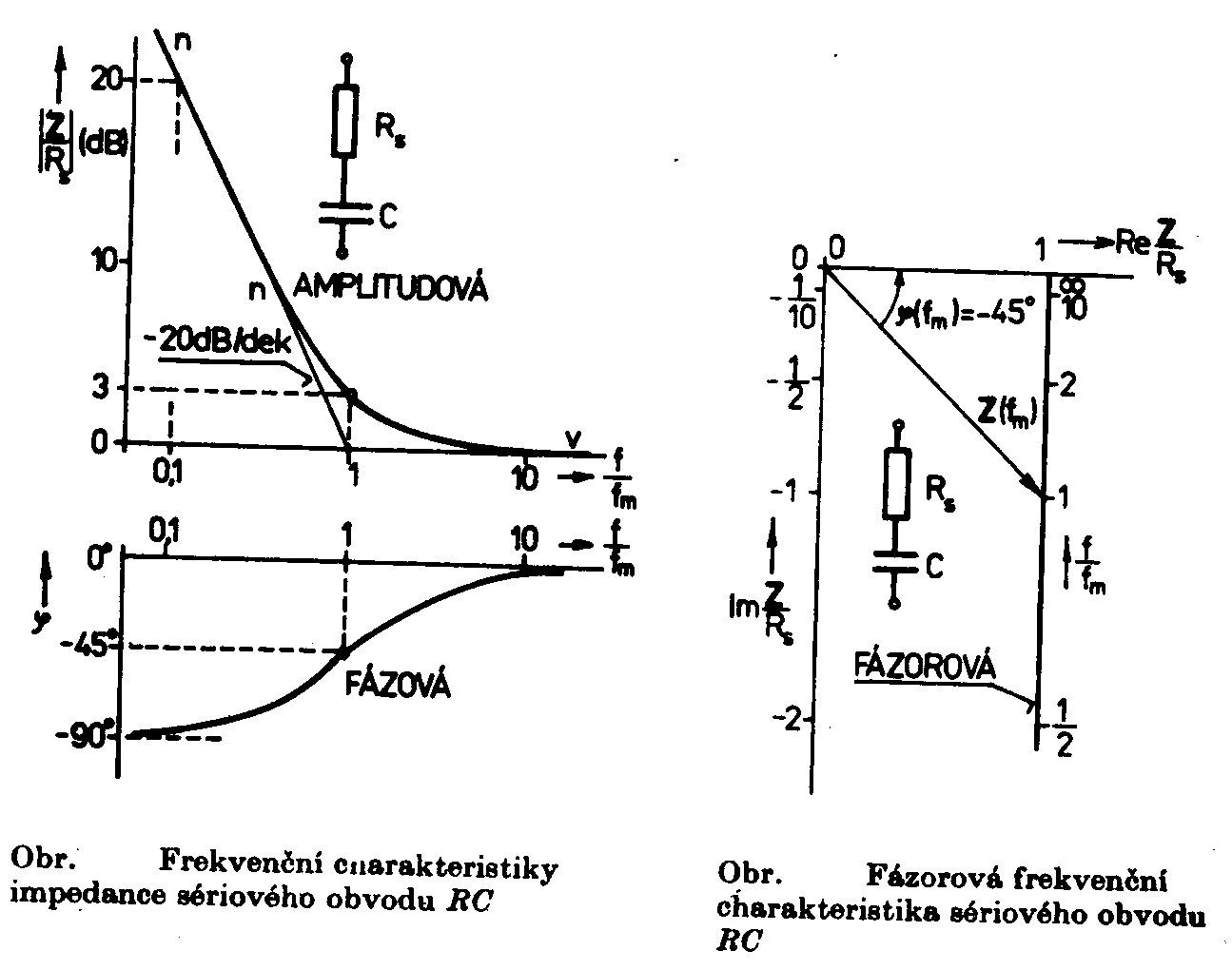
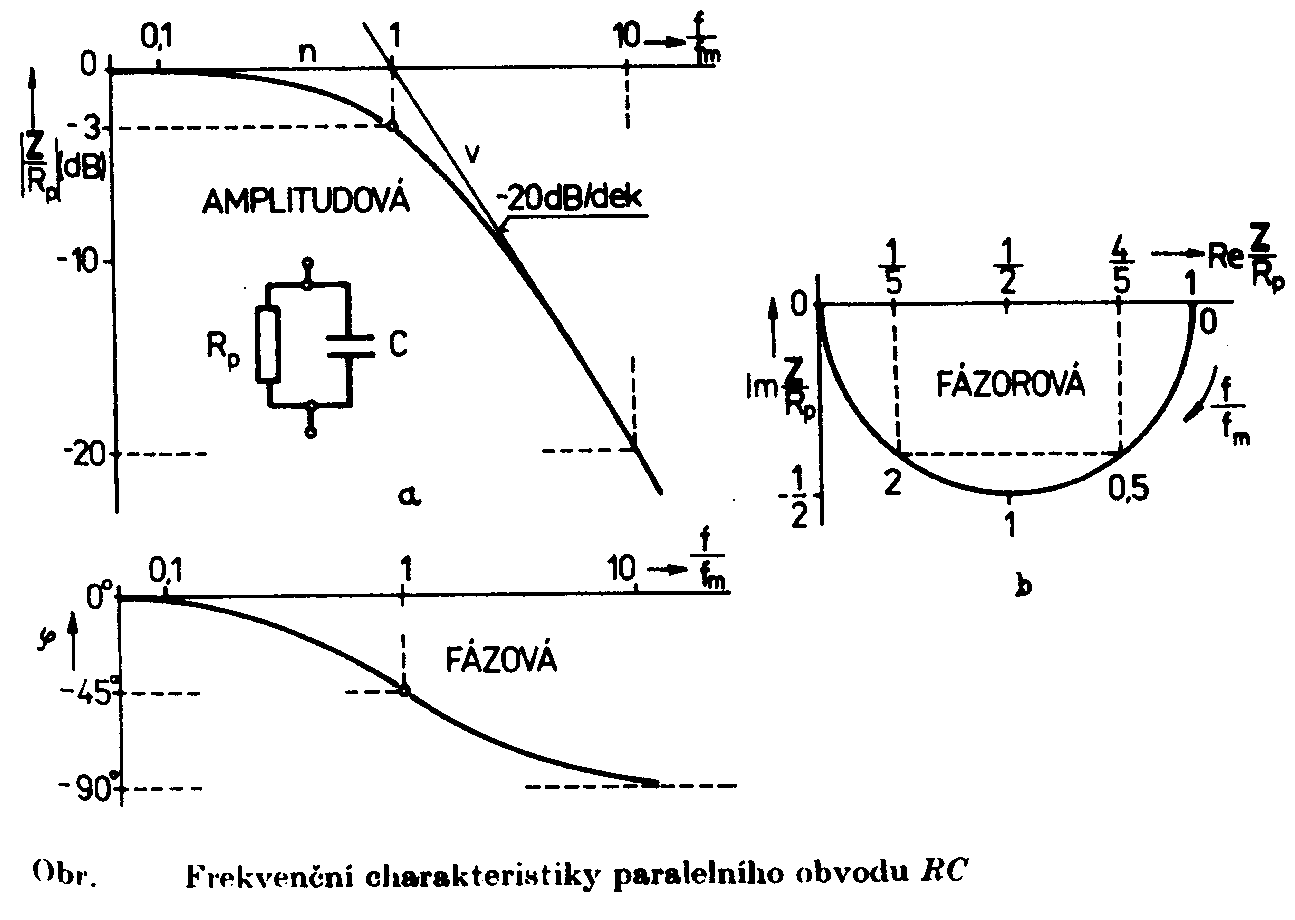
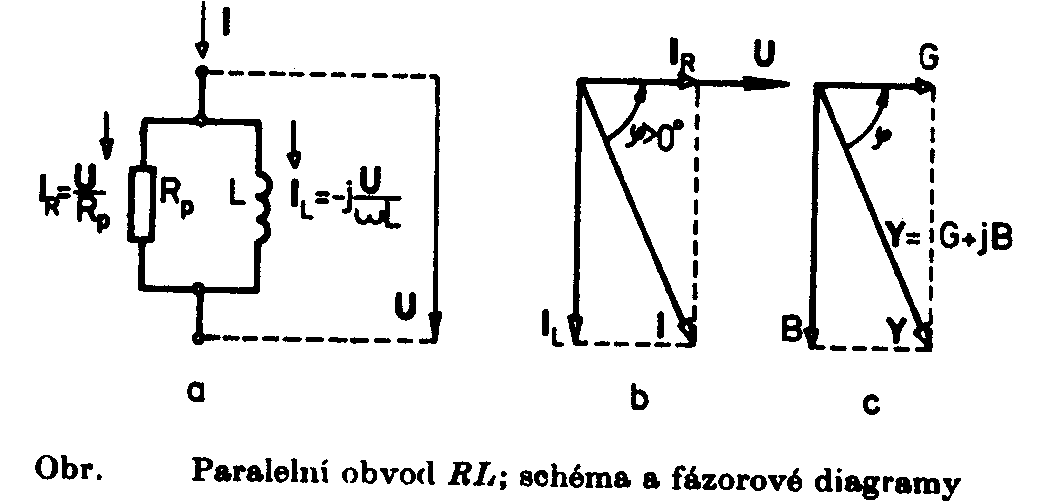
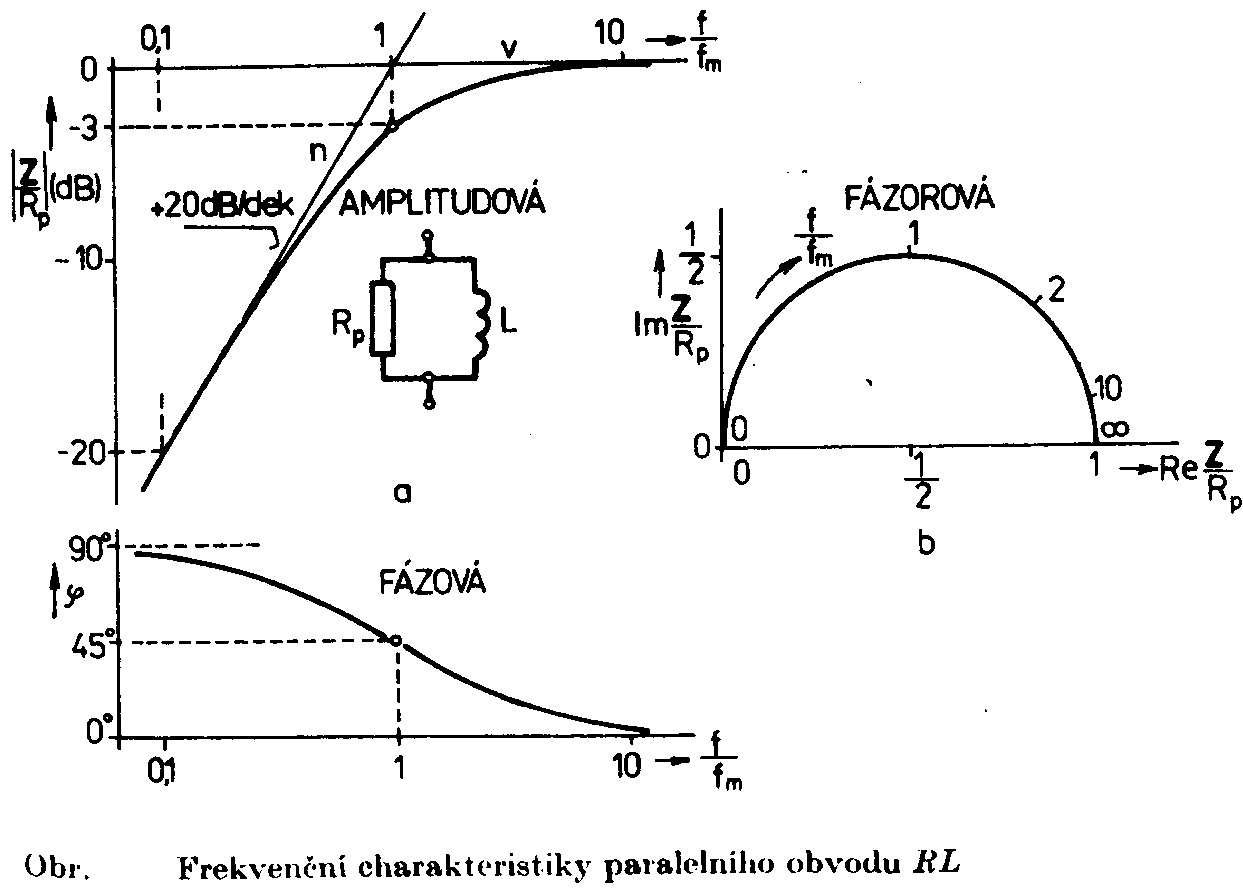
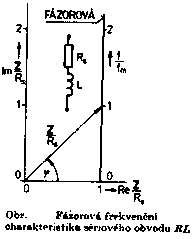
v decibelech Je zřejmé, že vztažné impedanci Zo odpovídá úroveň 0dB. Jiný, často používaný způsob, jak zachytit frekvenční závislost impedance jednobranu, je současný záznam absolutní hodnoty i fáze formou fázorové frekvenční charakteristiky v Gaussově komplexní rovině. Frekvenční charakteristika je v této rovině tvořena čarou spojující koncové body fázorů impedancí nakreslených pro jednotlivé frekvence. Lze ji sestrojit bod po bodu ze známých |Z| a j a pro určitou frekvenci nebo ze známých hodnot R a X pro určitou frekvenci, popřípadě je možné napsat její rovnici analyticky. Sériový obvod RLZ = RS + jwL Za vztažnou hodnotu zvolíme odpor RS a platí : Z / RS = 1 + jwL / RS (poměrná impedance) Poměrnou impedanci upravíme : Určíme absolutní hodnotu a fázový posun v závislosti na poměrné frekvenci : Frekvenční charakteristiku absolutní hodnoty poměrné impedance kreslíme v dB podle vztahu Svislá osa má lineární stupnici v dB, vodorovná osa je logaritmická. Přímky jsou asymptoty k frekvenční charakteristice absolutní hodnoty poměrné impedance. Zvětšíme-li frekvenci na desetinásobek, zvětší se poměrná impedance o 20dB. Sériový obvod RCZ = RS – j 1/wC Za vztažnou hodnotu zvolíme odpor RS a platí : Z / RS = ( wRSC - j ) / wRSC ( poměrná impedance ) Poměrnou impedanci upravíme : Určíme absolutní hodnotu a fázový posun v závislosti na poměrné frekvenci : Frekvenční charakteristiku absolutní hodnoty poměrné impedance kreslíme v dB podle vztahu Svislá osa má lineární stupnici v dB, vodorovná osa je logaritmická. Přímky jsou asymptoty k frekvenční charakteristice absolutní hodnoty poměrné impedance. Paralelní obvod RCZ = RP / ( 1 + jwCRP ) Za vztažnou hodnotu zvolíme odpor RP a platí : Z / RP = 1 / ( jwRPC ) (poměrná impedance) Poměrnou impedanci upravíme : Určíme absolutní hodnotu a fázový posun v závislosti na poměrné frekvenci : Frekvenční charakteristiku absolutní hodnoty poměrné impedance kreslíme v dB podle vztahu Svislá osa má lineární stupnici v dB, vodorovná osa je logaritmická. Přímky jsou asymptoty k frekvenční charakteristice absolutní hodnoty poměrné impedance. Paralelní obvod RLZ = (RP . jwL) / (RP + jwL) = (jwL) / (1+jw (L / RP)) Za vztažnou hodnotu zvolíme odpor RP a platí : Z / RP = (jwL / RP) / (1 + jwL / RP) ( poměrná impedance ) Poměrnou impedanci upravíme : Určíme absolutní hodnotu a fázový posun v závislosti na poměrné frekvenci : Frekvenční charakteristiku absolutní hodnoty poměrné impedance kreslíme v dB podle vztahu Svislá osa má lineární stupnici v dB, vodorovná osa je logaritmická. Přímky jsou asymptoty k frekvenční charakteristice absolutní hodnoty poměrné impedance. Zvětšíme-li frekvenci na desetinásobek, zmenší se poměrná impedance o 20dB. |
|
zpět na předchozí stránku
Copyright © 2003 Hell
doporučené rozlišení 1024x768