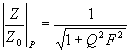|
|
HŘÍŠNÍCI NOVÝ UŽIVATEL nepřihlášený uživatel Právě si tyto stránky čte 1 člověk. |
|
Poslední změna:
29.09.2007 |
|
Návštěvník číslo: 26421 |
| ICQ:61783389 |
|
Copyright © 2003 Hell |
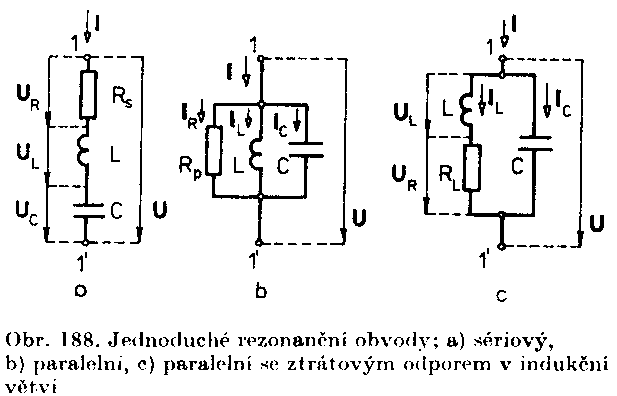
ElektronikaMaturitní otázkyJEDNODUCHÉ REZONANČNÍ OBVODY16.Jednoduché rezonanční obvodyJednoduché rezonanční obvody vznikají spojením rezistoru s činným odporem, cívky a kondenzátoru jedním ze způsobů nakreslených na obr. 188. Je zřejmé, že obvod vytvořený kterýmkoli z uvedených způsobů je opět komplexní jednobran, avšak při jedné, tzv. rezonanční frekvence se v obvodu navzájem vyrovná působení indukční a kapacitní reaktance na fázový posun mezi celkovým proudem procházejícím do obvodu a napětím mezi svorkami 1,1'. Celý obvod se při této frekvenci chová jako činný odpor.
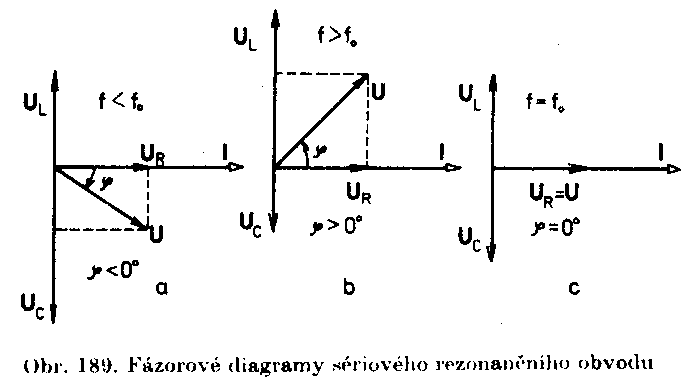
Stav obvodu, který nastane při rezonanční frekvenci se nazývá rezonance. Sériový rezonanční obvod Jak je naznačeno na následujícím obrázku, vyvolává procházející proud I na jednotlivých částech obvodu úbytky napětí UR, UL, UC, které můžeme vyjádřit vztahy UR = RS I UL
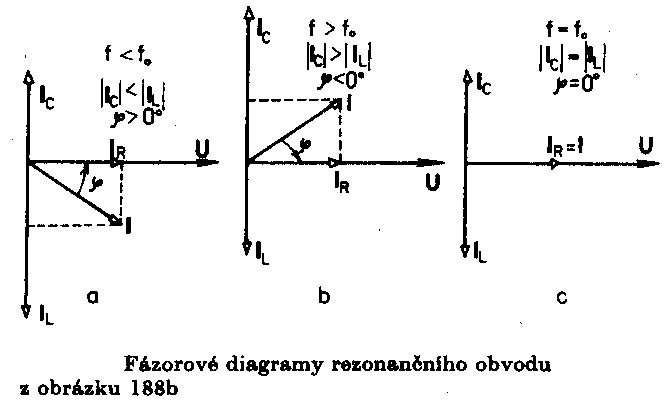
= jwLI UC = Odpovídající fázorové diagramy jsou na následujícím obrázku. Všimněme si toho, že při frekvenci f < fo je |UL| < |UC| a celkový fázový posuv j < 0 – impedance má kapacitní charakter. Při f > f0 je |UL| > |UC|,j > 0 – impedance má indukční charakter. Je-li f = f0, je obvod v rezonanci – |UL| = |UC| a j = 0.
Impedance obvodu Celková impedance sériového rezonančního obvodu se rovná Rezonanční frekvence Podle definice rezonance musí být pro w = w0 impedance Z reálná. To znamená, že její imaginární součet musí být pro tuto frekvenci rovna nule
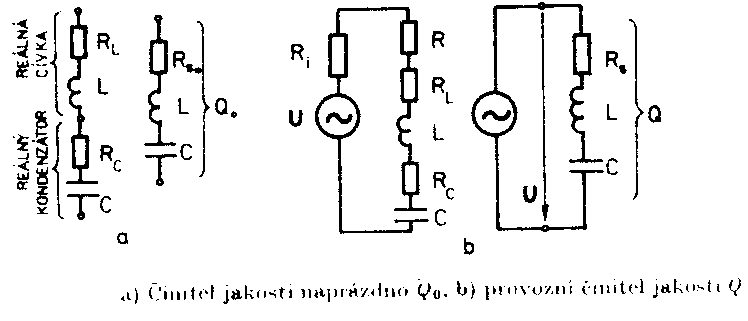
Odtud dostáváme Thompsonův vztah pro výpočet rezonanční frekvence w0 = Činitel jakosti sériového rezonančního obvodu V součástkách skutečného rezonančního obvodu vznikají při průchodu proudu ztráty. Tyto ztráty můžeme vzít v úvahu zařazením ztrátových odporů RL a RC do série s cívkou a kondenzátorem, které pak již považujeme za bezeztrátové. Oba odpory dohromady dávají ztrátový odpor RS0 = RL + RC, jehož pomocí definujeme pro rezonanční frekvenci činitel sériového obvodu naprázdno Q0. Q0=
Kdybychom znali pro frekvenci f0 činitel jakosti cívky Ql a kondenzátoru Qc = 1 / tg d, mohli bychom, jak lze dokázat dosazením do následujícího vztahu, vypočítat Q0 celého obvodu ze vztahu
V provozních podmínkách, kdy je obvod napájen ze zdroje signálu s vnitřním odporem Ri, popř. je-li v sérii s cívkou a kondenzátorem další rezistor R, působí všechny sériové odpory na vlastnosti obvodu souhlasně a tvoří dohromady již dříve popsaný odpor Rs Rs = Rs0 + R + Ri Činitel
jakosti, respektující všechny tyto odpory, se nazývá provozní činitel jakosti.
Můžeme ho vypočítat ze vztahu : Q = Protože Rs je větší než Rso, je činitel jakosti Q menší vždy než činitel jakosti Qo. Z předcházející úvahy plyne důležitý požadavek pro praxi: Abychom vlivem vnitřního odporu zdroje příliš nezmenšili činitel jakosti, musíme sériové rezonanční obvody napájet ze zdrojů s malým vnitřním odporem. Rezonanční impedance Z definice rezonance plyne, že při rezonanční frekvenci je celková impedance obvodu reálná. Označuje se Zo a nazývá se rezonanční impedance. Zřejmě platí Z0 = Rs Působí-li v rezonanci na celém obvodu napětí U, je proud procházející do obvodu a napětí na jednotlivých reaktancích V rezonanci je na obou reaktancích Q-krát větší napětí, než je na celém sériovém rezonančním obvodu. Tohoto principu využívá přístroj Q-metr. Rezonanční křivka sériového rezonančního obvoduNakreslíme-li frekvenční závislost absolutní hodnoty impedance sériového rezonančního obvodu Z získáme jedno z možných znázornění jeho rezonanční křivky. Obrázek ukazuje rezonanční křivky tří obvodů s různými rezonančními frekvencemi a činiteli jakosti. Dohře ale povšimněte toho, že obvody, které mají velký činitel jakosti Q, mají křivku úzkou, minimum impedance v rezonanci je ostře vyjádřeno a rezonanční impedance je malá. Zcela obráceně je tomu u obvodů s malým činitelem jakosti Q. Šířka pásma rezonančního obvoduŠířka pásma B je veličina
důležitá při použití rezonančních obvodů v praxi. Je to frekvenční rozdíl
f2 - f1, odpovídající určité domluvené změně impedance
obvodu vzhledem k impedanci Z0. Často se definuje pro změnu
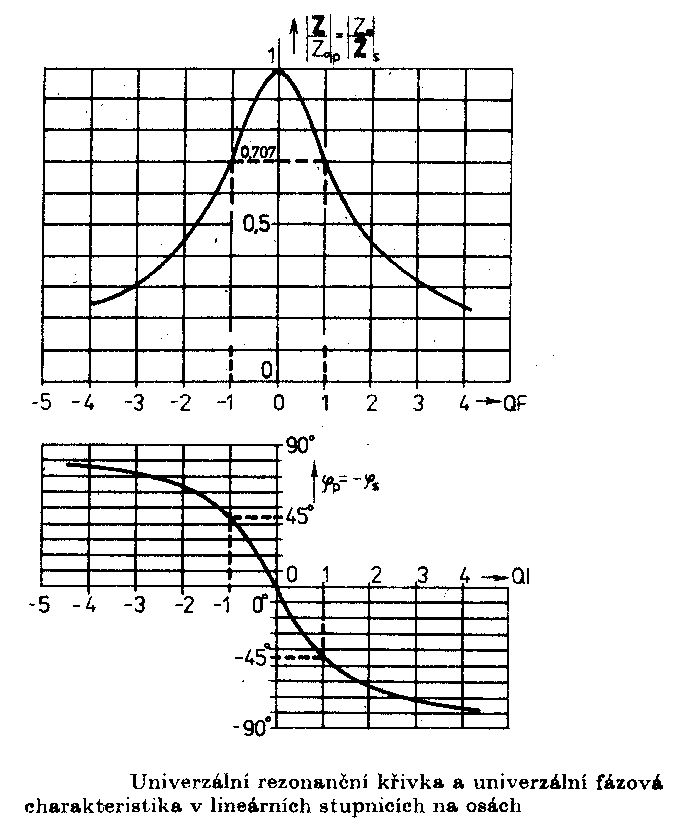
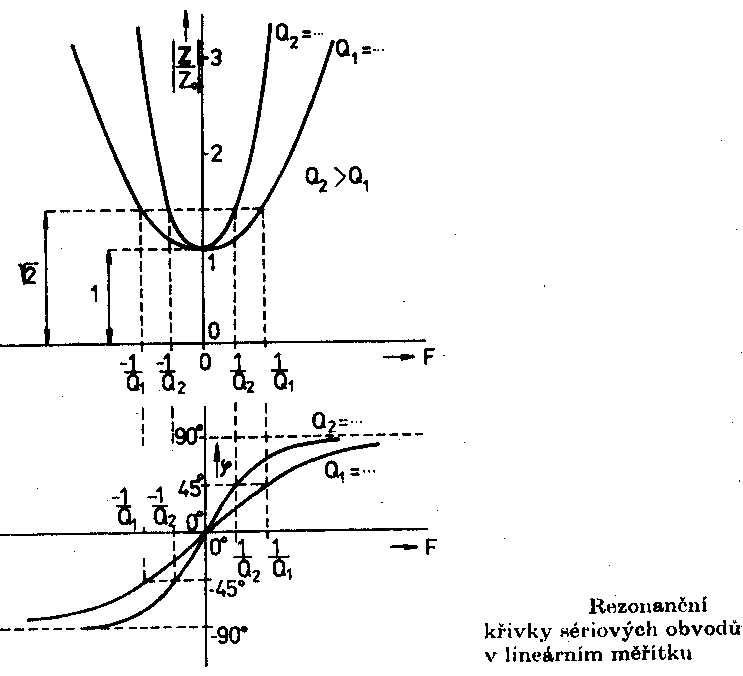
impedance o 3dB, tj. pro velikost |Z| = Z0 Poměrné vyjádření rezonanční křivkya) poměrné znázornění b) poměrné rozladění Abychom mohli snadno porovnávat vlastnosti jednotlivých rezonančních obvodů, znázorňujeme jejich rezonační křivky v poměrném měřítku. V praxi se nejčastěji používá vyjádření rezonanční křivky pomocí poměrného rozladění. F = Pro rezonanční frekvenci je F = 0. Při f = 0 je F = -¥ s při f = ¥ je F = +¥. Známe-li velikost poměrného rozladění F, můžeme vypočítat odpovídající frekvenci ze vztahu Který lze získat výpočtem frekvence f z definiční rovnice pro poměrné rozladění F. Odvozením dostaneme vztah Tento vztah představuje rovnici poměrné impedance obvodu v komplexním tvaru. Další vztah je rovnice poměrné rezonanční křivky. Fáze je fázová charakteristika sériového rezonančního obvodu.
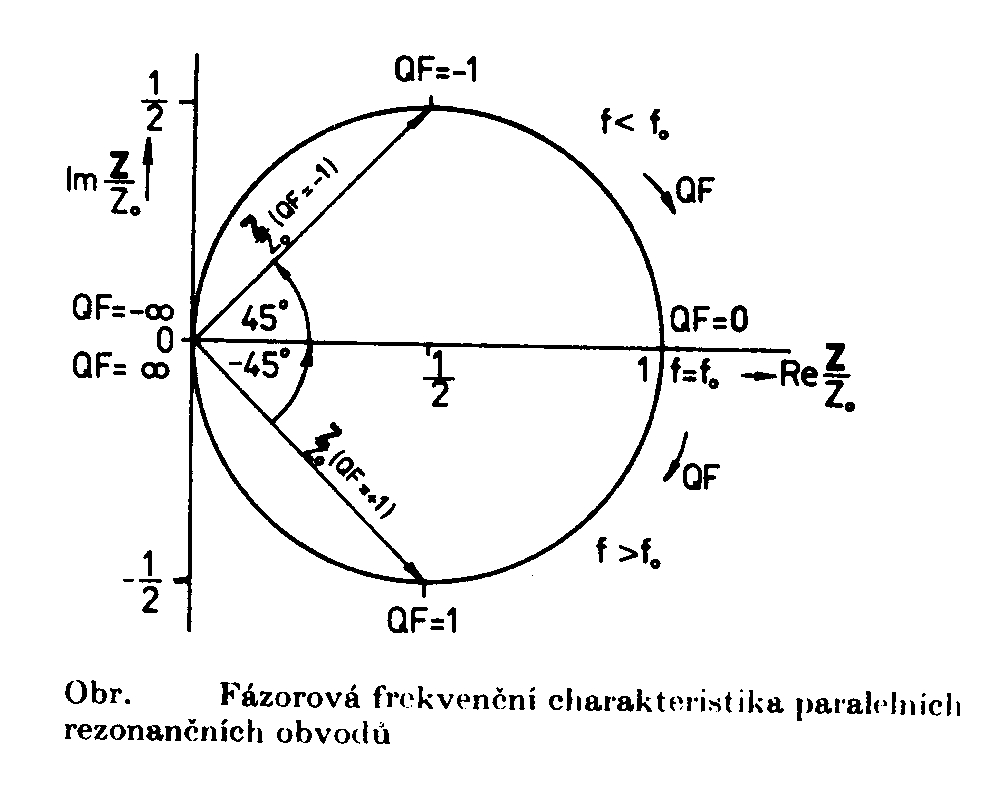
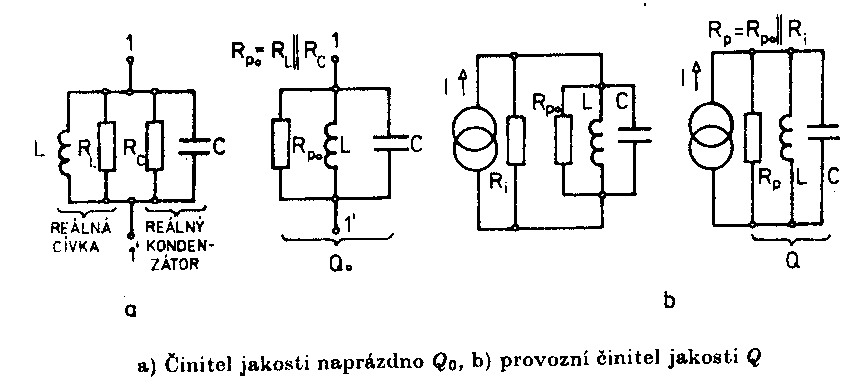
Rezonanční křivka vychází v tomto znázornění souměrná kolem svislé osy nakreslené v rezonanční frekvenci. Změna poměrné impedance o 3dB nastane pro QF = ±1, takže okrajům pásma odpovídají poměrná rozladění a fázové úhly ±45o. Paralelní rezonanční obvodNapětí U, působící mezi svorkami 1, 1' paralelního obvodu, vytváří celkový proud I, který se dělí na proudy jednotlivých větví. Pro obvod nakreslený dále platí První obrázek je kreslen pro f < fo - fázový posun je kladný a obvod má indukční charakter. Druhý obrázek je pro frekvenci f > fo. Fázový posun je záporný a obvod má kapacitní charakter. Třetí obrázek je při rezonanci a pak |IL| = |IC| a j = 0. Položíme-li Im Y = 0 a w = w0 odtud odvodíme pro rezonanční frekvenci stejný vztah jako pro obvod sériový w0= Činitel jakosti paralelního rezonančního obvodu Ztráty vyjadřujeme paralelními ztrátovými odpory cívky a kondenzátoru. V praxi je obvod připojen
ke zdroji s vnitřním odporem Ri a k zátěži Rz.
Tyto odpory tvoři vnější tlumící odpor kde Rp je paralelní kombinace odporů Rp0 a Rtl. Porovnáním Q a Q0 dostaneme ze kterého plyne Oba poslední vztahy lze použít i v případech, kdy jde o připojení dalšího tlumícího rezistoru k rezonančnímu obvodu. Místo činitele jakosti Q0 dosazujeme provozní činitel jakosti Q Cirkulační proud v cívce a kondenzátoru v rezonanci Rezonanční impedance Zo
= Rp. Působí-li na obvodu napětí U je celkový proud procházející
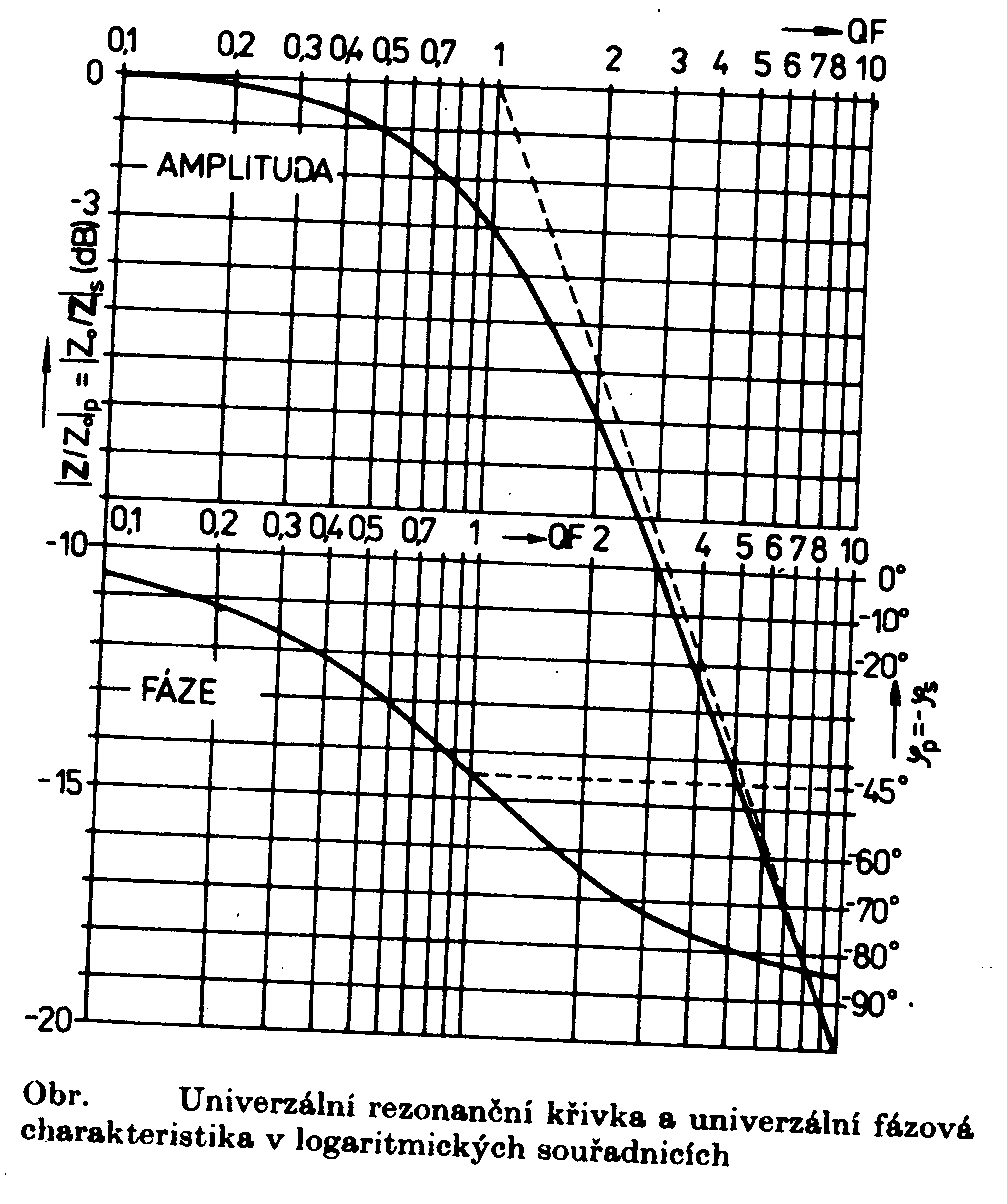
obvodem v rezonanci Zároveň prochází indukční větví proud a kapacitní větví proud Rezonanční křivkaNejčastěji požíváme poměrné vyjádření rezonanční křivky pomocí rozladění F F= Odpovídající rovnici získáme z admitance Výpočtem dostaneme Průběhy získané výpočtem jsou na následujícím obrázku. Šířka pásmaŠířka pásma je rozdíl frekvencí, odpovídající domluvené změně impedance obvodu proti impedanci rezonanční. Většinou se užívá změna o 3dB. Odvozený vztah se také často používá pro určení činitele jakosti z naměřené rezonanční křivky, neboť Selektivnost obvoduSchopnost rezonančního obvodu vybrat z mnoha frekvencí tu, na kterou je obvod naladěn se nazývá selektivnost obvodu. Číselně se selektivnost určuje poměrem Další kritériem dovolujícím posoudit selektivnost obvodu je strmost boků rezonanční křivky. Její mírou je k, který porovnává šířku pásma obvodu při poklesu jeho impedance o 60dB s šířkou pásma poklesu o 6dB. Pro obvody s velkým činitelem jakosti je činitel tvaru křivky definován vztahem Pro obvody s menším činitelem jakosti pak Jak můžeme zjistit dosazením do posledních dvou vztahů, mají všechny jednoduché rezonanční obvody stejný činitel tvaru rezonanční křivky . Znamená to, že při určité požadované šířce pásma a dané rezonanční frekvenci jsou již tvar rezonanční křivky i selektivnost obvodu zcela určeny a není možné je bez ovlivnění B nebo fo změnit. V mnoha případech jsou na selektivnost obvodů, kterými prochází signál, kladeny tak velké požadavky, že jo není možné splnit použitím jednoduchých rezonančních obvodů, (Např. obvody pracující v mezifrekvenčních zesilovačích rozhlasových přijímačů, v různých filtrech ve sdělovací technice po vedeních, v mnoha měřicích přístrojích atd.) V těch případech používáme obvody, u kterých je možné měnit strmost boků frekvenční charakteristiky absolutní hodnoty impedance nezávisle na šířce požadovaného frekvenčního pásma a na velikosti frekvencí, které obvodem procházejí. Příkladem jsou vázané rezonanční obvody. Velmi selektivní obvody mají frekvenční charakteristiku absolutní hodnoty impedance blízkou obdélníku. Činitel tvaru k jejich frekvenční charakteristiky je jen o málo větší než 1. Univerzální rezonanční křivka ( pro SRO a PRO )Vztahy pro absolutní hodnotu a fázi poměrné impedance PRO Jak plyne z obrázku rezonanční křivky a fázových charakteristik PRO, je možné pomocí těchto rovnic nakreslit pro každý činitel jakosti samostatný průběh rezonanční křivky a fázové charakteristiky. Vyneseme-li však na vodorovnou osu místo poměrného rozladění F součin QF, získáme pro všechny paralelní rezonanční obvody univerzální průběhy, které jsou znázorněny na následujícím obrázku, jsou stejné závislosti vyjádřeny v decibelech, a logaritmickou stupnicí na vodorovné ose. Napišme vedle sebe vztahy pro absolutní hodnotu a fázi poměrné impedance paralelních (použijeme zde pro rozlišení index p) a sériových (index s) rezonančních obvodů. jp = - arctg QF js = - arctg QF Ze vzájemného porovnání odpovídajících vztahů plyne, že absolutní hodnota poměrné impedance sériových obvodů je převrácenou hodnotou absolutní hodnoty poměrné impedance obvodů paralelních. Fázové úhly pro stejná rozladění obou obvodů se liší pouze znaménkem. Zobrazení frekvenční závislosti poměrné impedance rezonančních obvodů v Gaussově rovině Pro sériový obvod bylo odvozeno
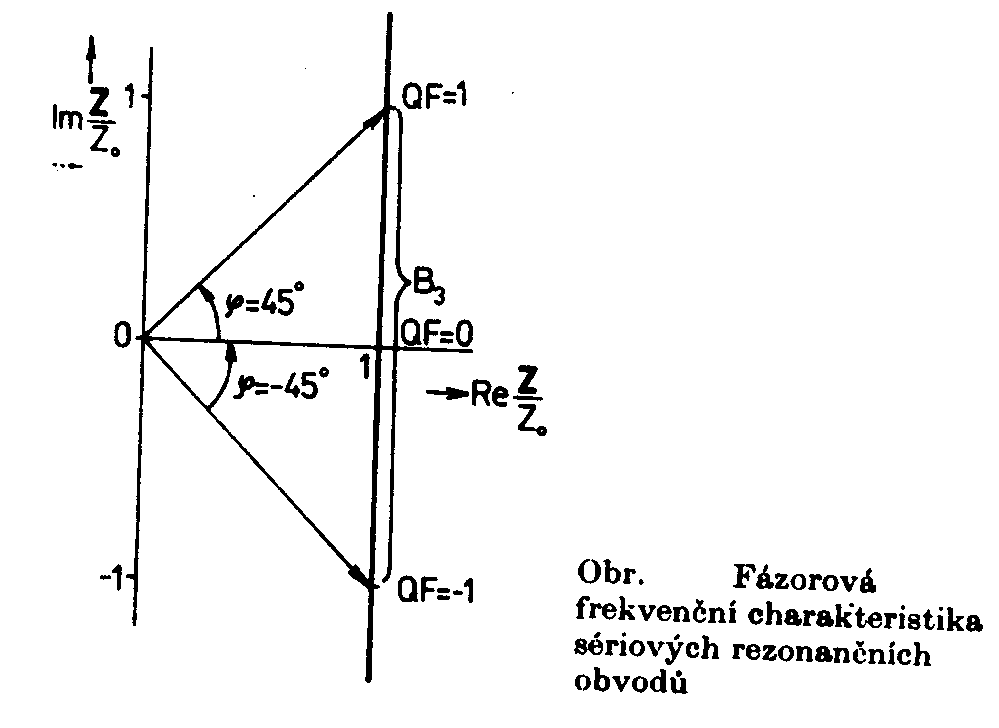
Reálná část se rovná jedné. Proto bude frekvenční závislost Z / Zo v Gaussově rovině představována přímkou rovnoběžnou se svislou osou a procházející bodem 1 na reálné ose. Ze vztahu Dosazením do těchto bodů získáme souřadnice bodů v Gaussově. Jde o kružnici se středem v bodě 1/2 na reálné ose a s poloměrem 1/2. |
|
zpět na předchozí stránku
Copyright © 2003 Hell
doporučené rozlišení 1024x768

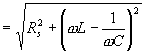
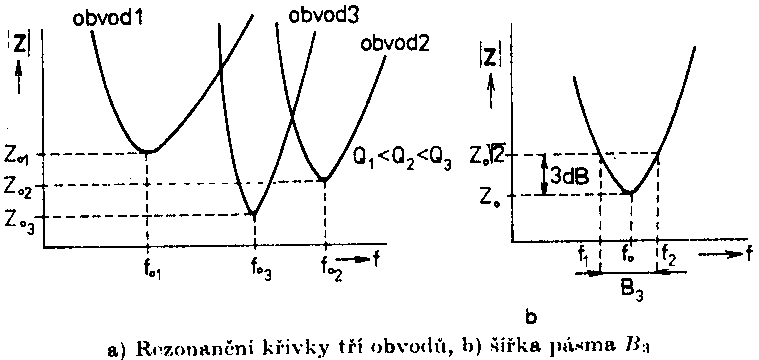
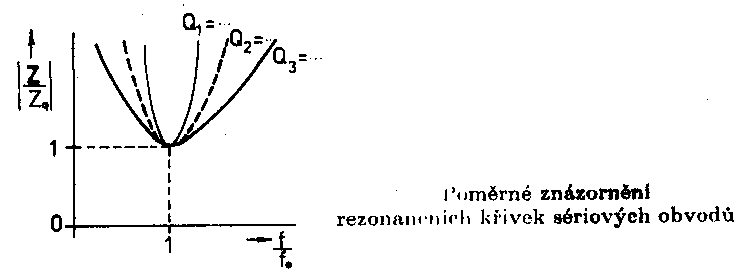
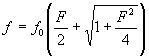
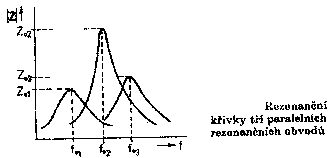
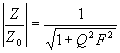 a
a 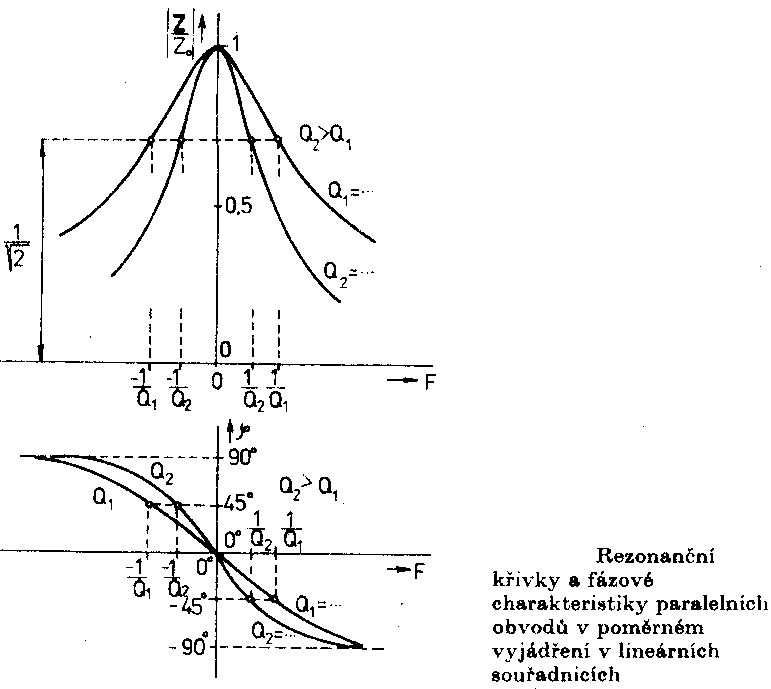
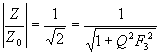
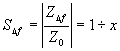
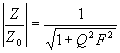 a
a