
|
|
HŘÍŠNÍCI NOVÝ UŽIVATEL nepřihlášený uživatel Právě si tyto stránky čte 1 člověk. |
|
Poslední změna:
29.09.2007 |
|
Návštěvník číslo: 26421 |
| ICQ:61783389 |
|
Copyright © 2003 Hell |
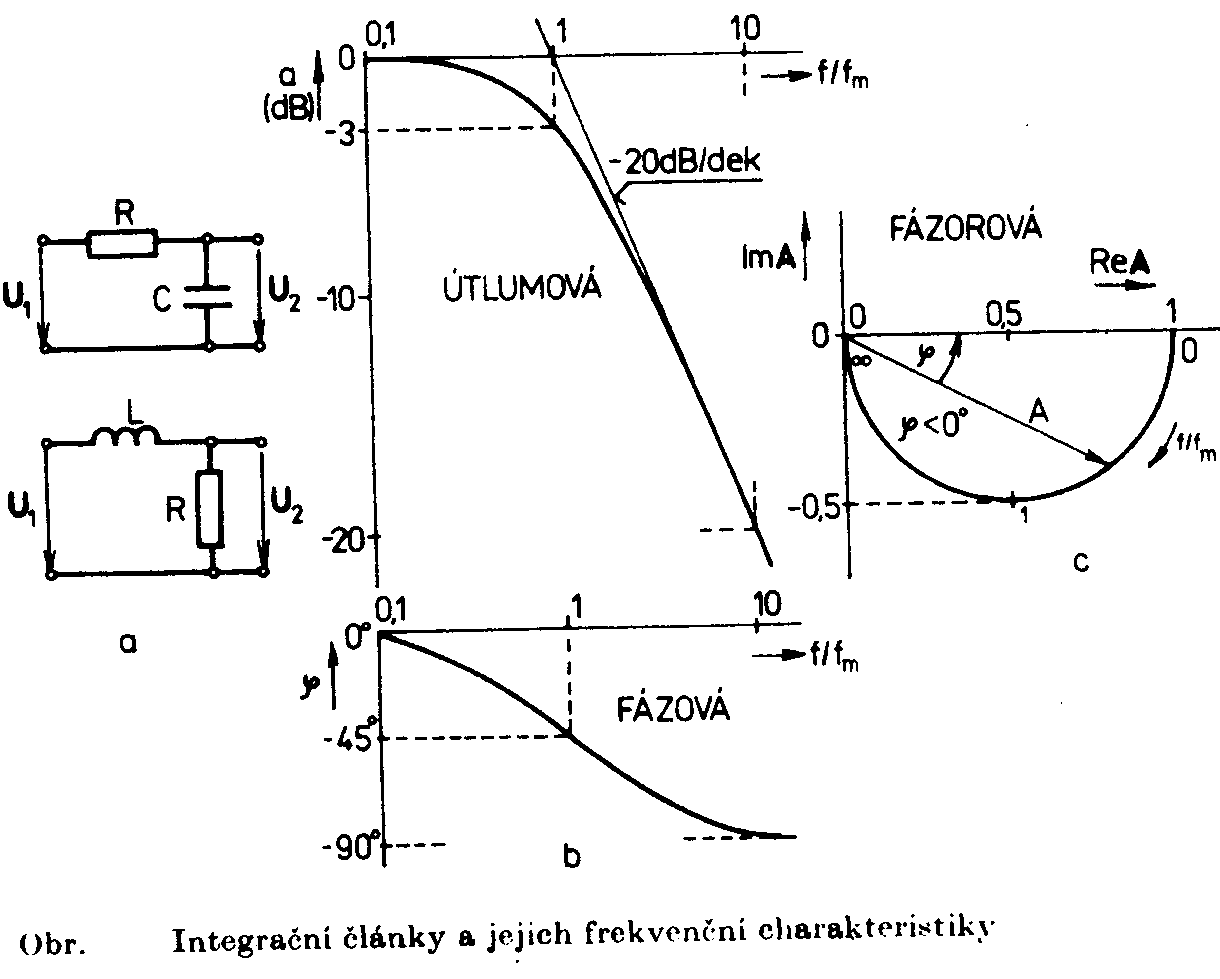
ElektronikaMaturitní otázkyKOMPLEXNÍ DVOJBRANY - PŘENOSOVÉ VLASTNOSTI17.Komplexní dvojbrany - přenosové vlastnosti Integrační a derivační článek RC patří mezi komplexní dvojbrany. Integrační článek má vlastnost dolnofrekvenční propusti, zatímco derivační má propust hornofrekvenční. U těchto článků je vždy důležitý napěťový přenos A . Je to poměr výstupního napětí ke vstupnímu. Přenos je závislý na kmitočtu A = |A|ejj . Je-li přenos větší než 1, jedná se o zesílení. V opačné případě dojde k útlumu. Dobrou představu o chování těchto dvojbranů nám dává grafické znázornění frekvenční závislosti na jeho přenosu. Přenos se zde obvykle vyjadřuje v decibelech a = 20 log |U2/U1| [dB] Integrační článek RC a RL nezatížený na výstupu : Přenos těchto článků odvodíme z poměru výstupního
napětí U2 a U1. Předpokládáme nulový vnitřní odpor zdroje
signálu a výstup článku naprázdno. Pro článek RC dostáváme Zavedením časových konstant
t =
RC a t = Dosazováním zvolených číselných hodnot za Derivační a článek RC a RL nezatížený na výstupu : Vzájemnou změnou rezistoru a kondenzátoru nebo cívky v zapojení článků integračních vzniknou články derivační. Jejich přenos opět odvodíme z poměru výstupního napětí U2 a vstupního napětí U1. Pro článek RC dostaneme
Integrační článek RC zatížený rezistorem V mnoha případech nelze zajistit činnost popisovaných
dvojbranů v podmínkách, ve kterých byl odvozen jejich přenos. Velmi často
jsou články zatěžovány obvody. Použitím Théveninovy poučky vzniknou obvody,
kde Zavedeme-li pro zjednodušení zápisu m = Derivační článek zatížený kondenzátorem Schéma překreslíme pomocí Théveninovy věty. Výsledkem zjednodušení
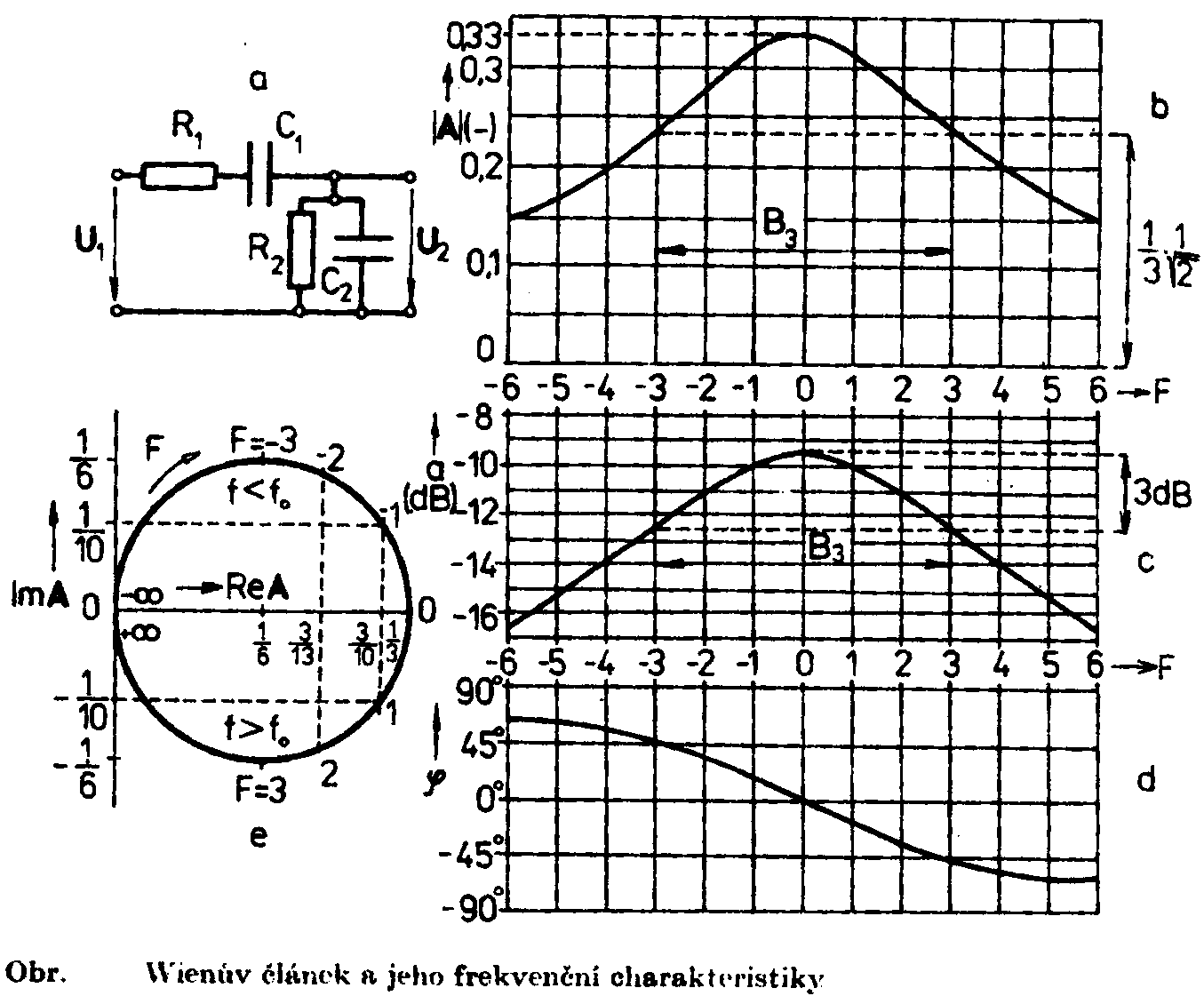
je obvod, kde platí Wienův článek Wienův článek je pásmová
propust. Napěťový přenos :
Rovnice útlumové charakteristiky
: Při kritické frekvenci f0 je reálný přenos :
Maximum přenosu při f0:
Nejčastěji se používají
W.články, ve kterých je R1=R2=R a C1=C2=C : Útlumová a fázová charakteristika je vyjádřena rovnicí: Odpovídající křivky jsou nakresleny na obr. Útlumová charakteristika je v lineární stupnici F souměrná podle svislé osy, procházející kritickou frekvencí (F=0). Této frekvenci odpovídá A=1/3 a j=0.Při změně frekvence se zmenšuje absolutní hodnota přenosu směrem k nule. Rozdíl frekvencí, který
odpovídá domluvené změně absolutní hodnoty přenosu proti její velikosti při
kritické frekvenci, se nazývá šířka pásma. Rozladění F3, pro která
poklesne |A| o 3dB prodi své max. hodnotě 1/3, vypočítáme z rovnice útlumové
char. : Z rovnice Články typu přemostěného článku T Je to pásmová zádrž RC. Přenos : Význam n plyne z obrázku. Kritická úhlová frekvence : Rovnice útlumové charakteristiky
: Rovnice fázové charakteristiky
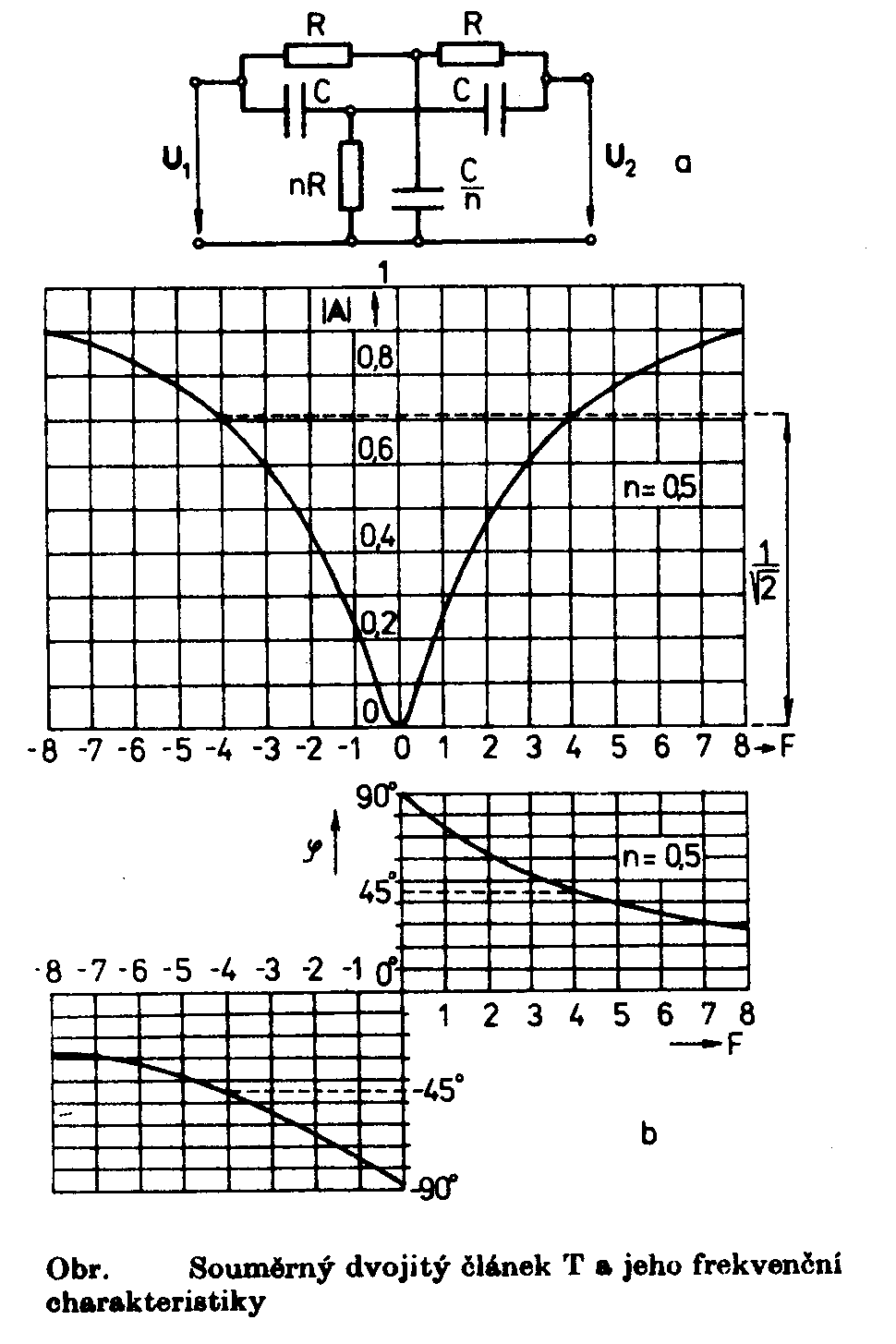
: Články typu dvojtého článku T Je to pásmová zádrž RC. Jde o souměrný dvojitý článek T, který je v praxi nejčastější. Kritická frekvence :
Zvolíme-li n=0,5 dostaneme
Pro symetrický dvojitý
článek T, který má n=0,5, je možné odvodit přenosovou rovnici v závislosti
na poměrném rozladění F ve tvaru Z tohoto vztahu plyne rovnice útlumové a fázové charakteristiky : Jejich průběhy jsou zakresleny
na obrázku. Při rozladění F=±4 je fázový posun j=±45o a absolutní hodnota přenosu
|
|
zpět na předchozí stránku
Copyright © 2003 Hell
doporučené rozlišení 1024x768

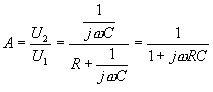 . Pro článek RL dostaneme
. Pro článek RL dostaneme 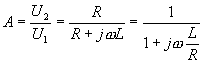
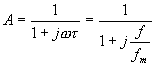 kde fm =
kde fm = 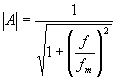 v decibelech
v decibelech
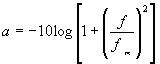 . Vypočteme
rovnici fázové chrakteristiky
. Vypočteme
rovnici fázové chrakteristiky 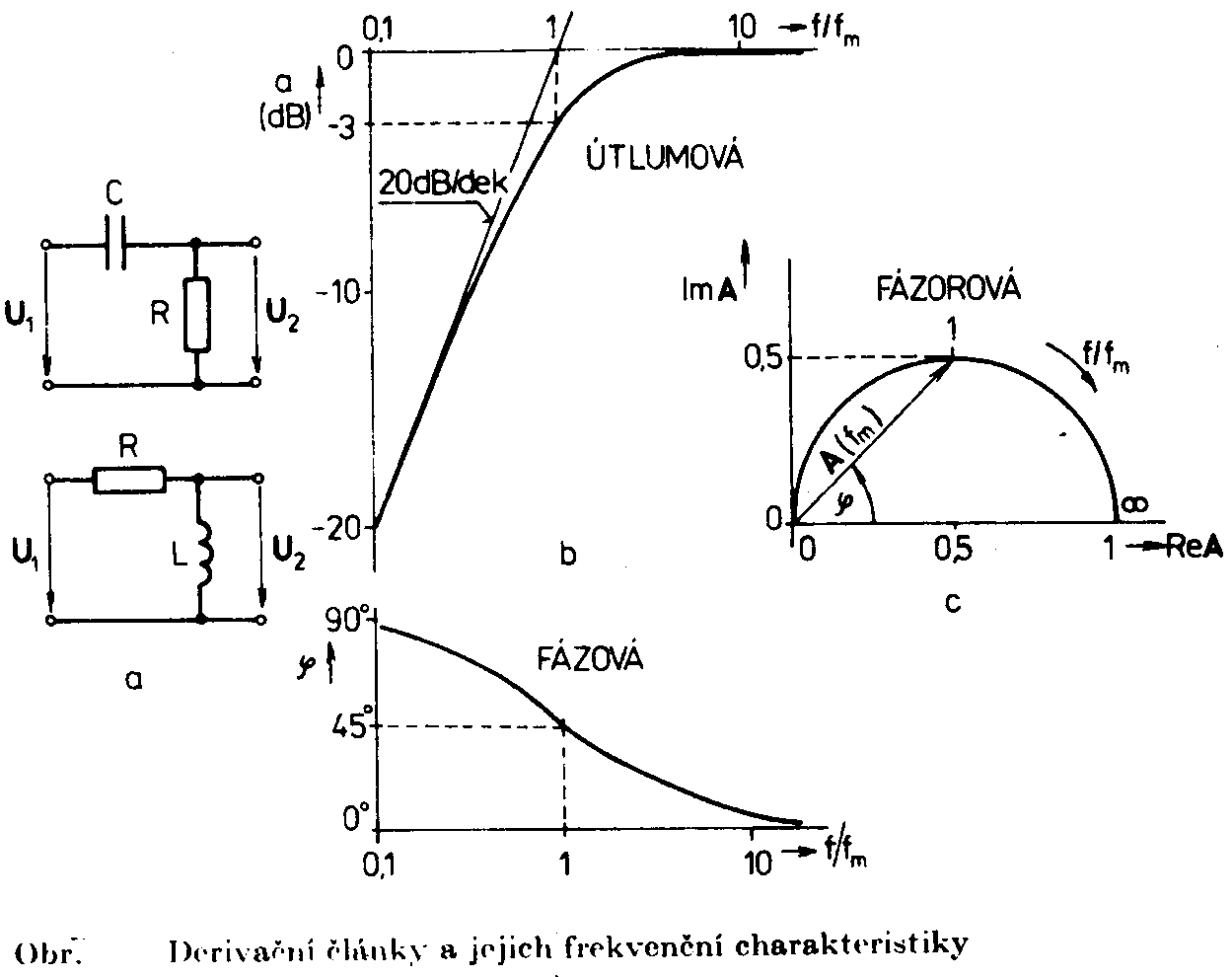
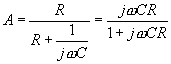 a
pro článek RL
a
pro článek RL 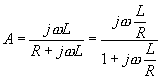 . Zavedením časové
konstanty
. Zavedením časové
konstanty 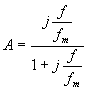 . Formálně stejným
způsobem, který byl použit pro integrační články, získáme pro derivační články
rovnici útlumové charakteristiky v prostém poměru
. Formálně stejným
způsobem, který byl použit pro integrační články, získáme pro derivační články
rovnici útlumové charakteristiky v prostém poměru 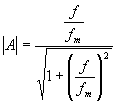 nebo v decibelech
nebo v decibelech
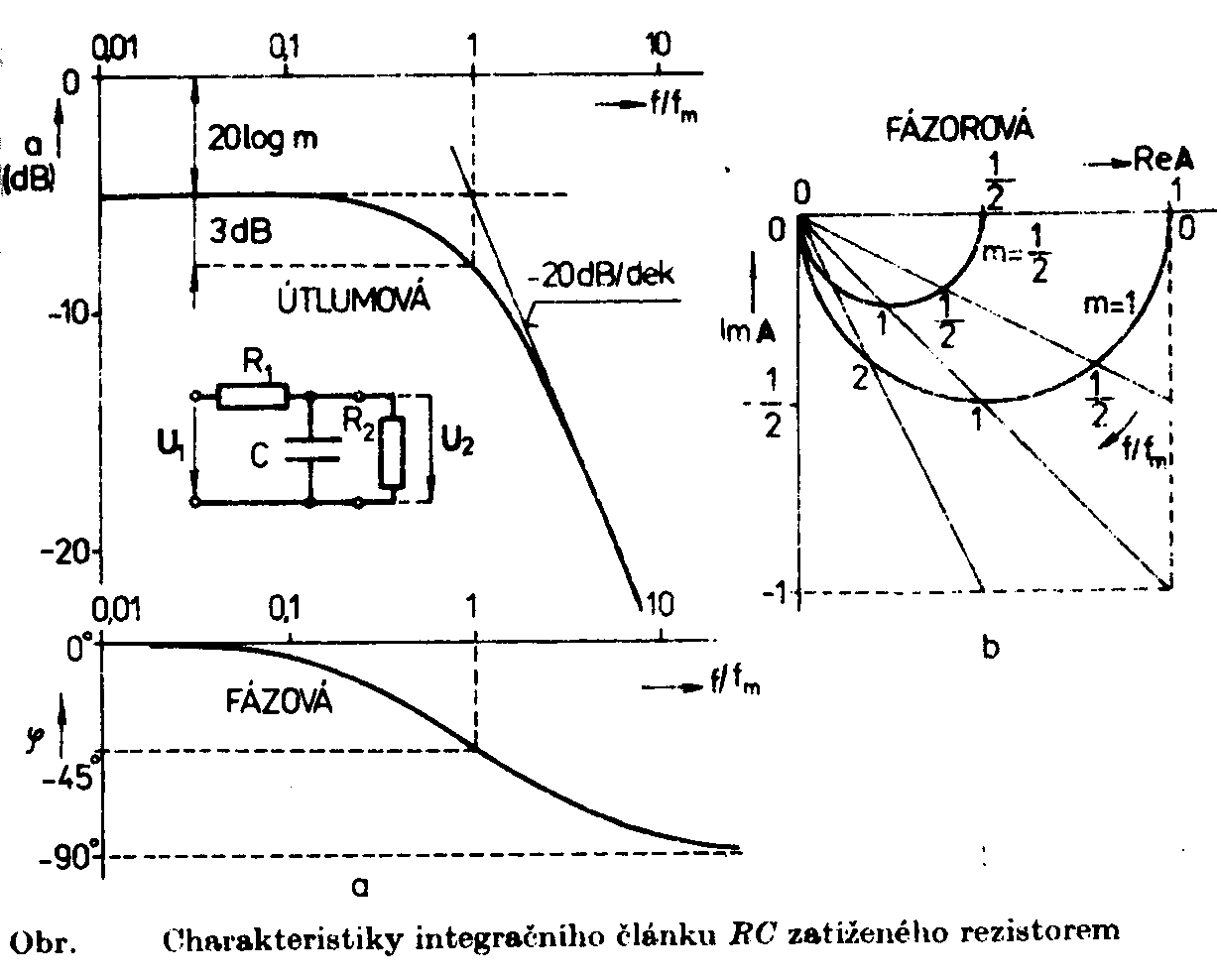
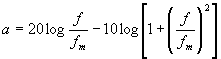 i rovnici fázové
charakteristiky
i rovnici fázové
charakteristiky 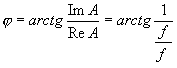 .
.
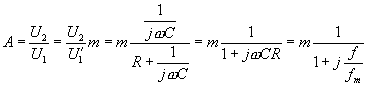 . Rovnice útlumové
charakteristiky v pravém poměru má tvar
. Rovnice útlumové
charakteristiky v pravém poměru má tvar 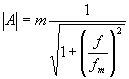 . V decibelech
. V decibelech
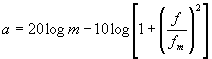 . Z tohoto
vztahu je zřejmé, že průběh útlumové charakteristiky sledovaného článku vyjádřený
v decibelech se skládá ze dvou částí. První není závislá na frekvenci a
je představována přímkou v úrovni 20 log m. Druhá je charakteristikou integračního
článku naprázdno. Obvyklým způsobem získáme rovnici fázové charakteristiky
. Z tohoto
vztahu je zřejmé, že průběh útlumové charakteristiky sledovaného článku vyjádřený
v decibelech se skládá ze dvou částí. První není závislá na frekvenci a
je představována přímkou v úrovni 20 log m. Druhá je charakteristikou integračního
článku naprázdno. Obvyklým způsobem získáme rovnici fázové charakteristiky
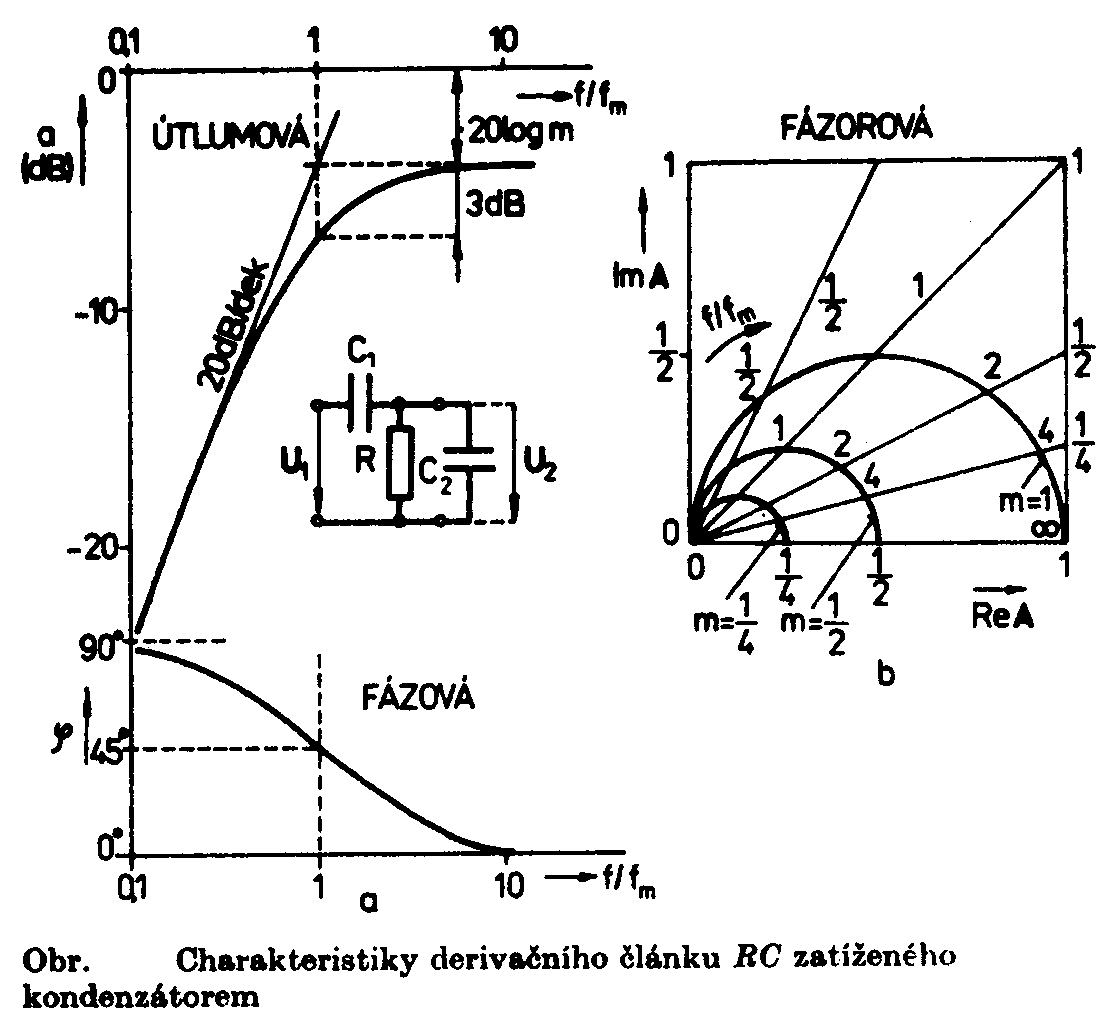
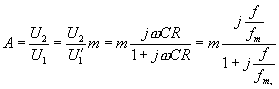 . Zde, stejně
jako v předcházejících případech, je fm =
. Zde, stejně
jako v předcházejících případech, je fm = 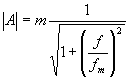 . V decibelech
dostáváme
. V decibelech
dostáváme 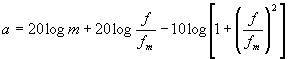 . Protože dělící
poměr m může dosáhnout nanejvýš jedné, je první, frekvenčně nezávislá část předcházejícího
vztahu představována vodorovnou přímkou v příslušné záporné úrovni. Zbývající
část vztahu pro a je útlumová charakteristika nezatíženého derivačního článku.
Časová konstanta je nyní
. Protože dělící
poměr m může dosáhnout nanejvýš jedné, je první, frekvenčně nezávislá část předcházejícího
vztahu představována vodorovnou přímkou v příslušné záporné úrovni. Zbývající
část vztahu pro a je útlumová charakteristika nezatíženého derivačního článku.
Časová konstanta je nyní 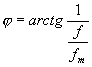 .
.
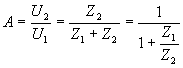
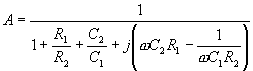
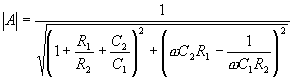
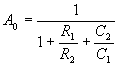
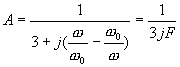
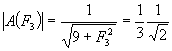 . Odtud plyne
pro okraj pásma B3 (obr b) F3
. Odtud plyne
pro okraj pásma B3 (obr b) F3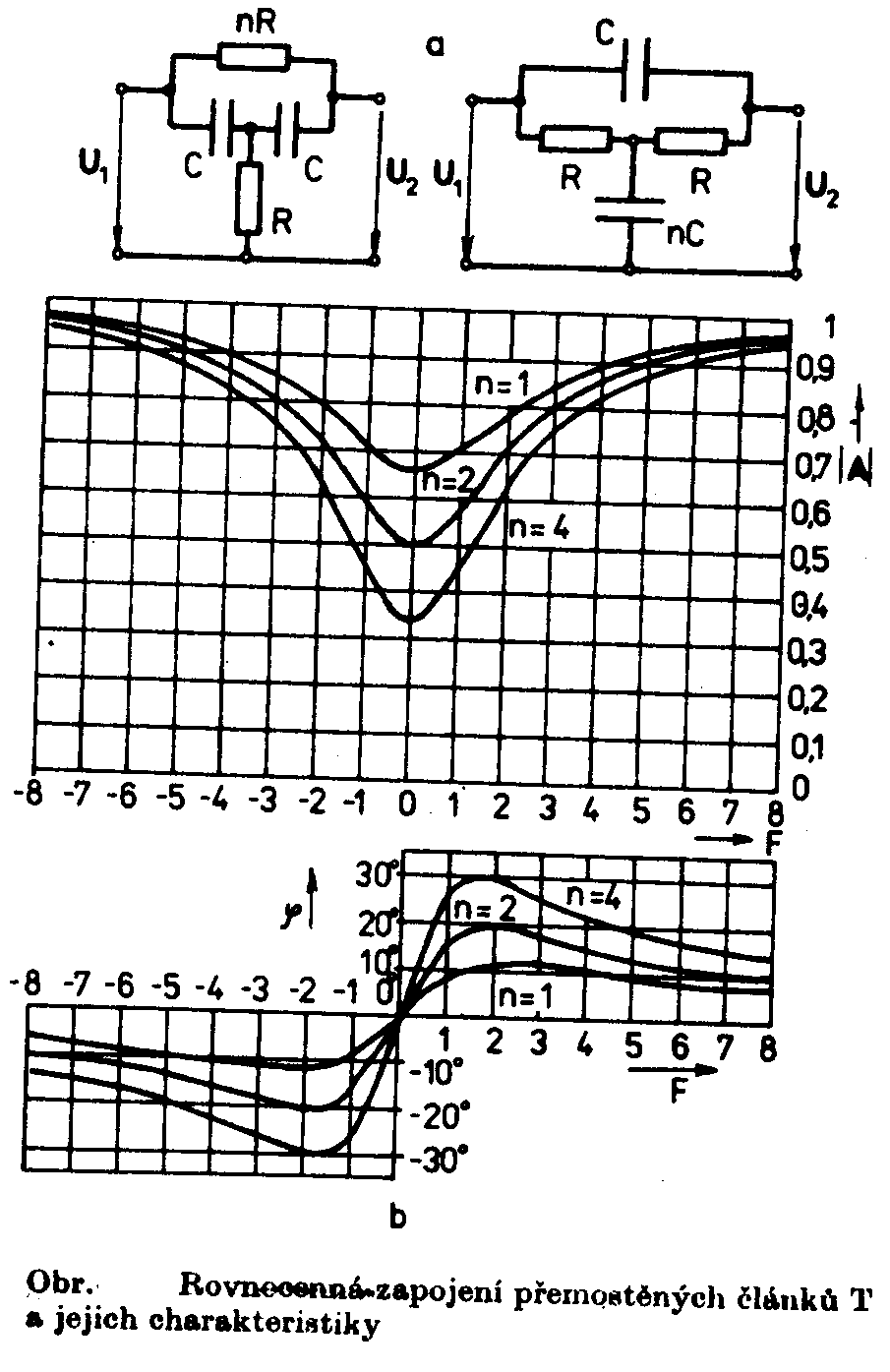
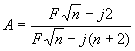
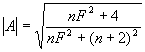
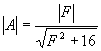 a
a