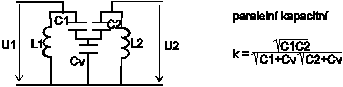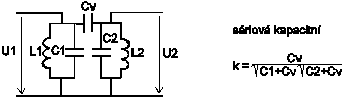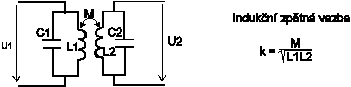
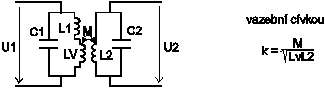
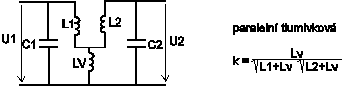
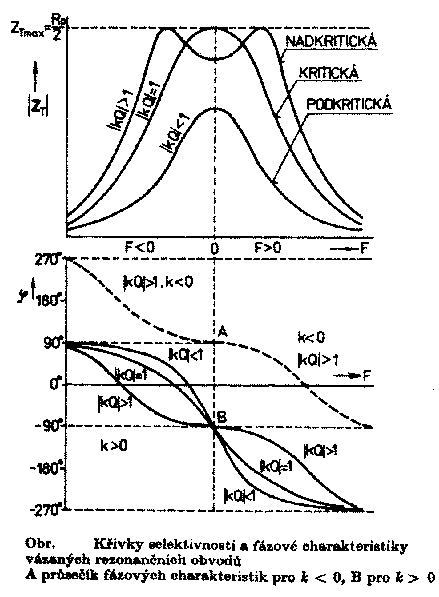
Elektronika

Maturitní otázky

VÁZANÉ REZONANČNÍ OBVODY

19.Vázané rezonanční obvody

Vázané rezonanční obvody patří do skupiny selektivních dvojbranů, které mají charakter pásmové propusti. Jsou tvořeny dvěma rezonančními obvody upravenými konstrukčně tak, aby část signálu primárního obvodu pronikala do sekundárního a naopak.

Zpětná vazba může mít několik druhů:

Velikost signálu pronikajícího z primárního do sekundárního obvodu a naopak se posuzována velikostí činitele vazby  k       

Zpětné vazby, které využívají vzájemné indukčnosti mají znaménko závislé na  směru vynutí cívek.

Kladná znaménka jsou pro M které je větší než nula. Kapacitní vazby  odpovídají indukčním vazbám kde M je menší než nula.

Všemi šesti základními druhy vazeb je možno dosáhnout v okolí rezonanční frekvence stejných vlastností  dvojice vázaných rezonančních obvodů. Podstatnější rozdíly pro jednotlivé zpětné vazby nastávají až při frekvencích značně vzdálených od rezonance.

V praxi se používají pouze vázané obvody, složené z rezonančních obvodů, které jsou naladěné na stejnou rezonanční frekvenci f₀. Pak se dvojice obvodů složená z různě tlumených obvodů chová jako by byla složena z obvodů se stejnými činiteli jakosti a stejnými tlumícími odpory. Jejich velikost lze vypočítat ze vzorců:

Nejdůležitější  veličinou, podle které lze posoudit vlastnosti dvojice vázaných obvodů je jejich přenosová

( tranzitní) impedance ZT která je definována vztahem:

Za U2 dosadíme velikost výstupního napětí sekundárního obvodu.

Za I1 vstupní proud primárního obvodu.

Grafickým znázorněním frekvenční závislosti absolutní hodnoty přenosové impedance jsou křivky selektivnosti dvojice vázaných obvodů.Fázová charakteristika dvojice je frekvenční závislost fázového posunu fázoru ZT. Poměrně pracným odvozením by bylo možno získat pro přenosovou impedanci rovnici.

Platnou přesně pro frekvence blízké rezonanci, ze které plyne důležitý závěr: Při rezonanci, kdy F=0, vykazuje fázor přenosové impedance K je větší 0 fázový posun - 90 stupňů. To zn., že výstupní napětí je při rezonanci opožděno proti vstupnímu proudu o čtvrtinu periody. Protože jsou při rezonanci vstupní proud a napětí na primárním rezonančním obvodu ve fázi, je napětí na sekundárním obvodu posunuto o zmíněných - 90 stupňů proti napětí na obvodu primárním.

Součin kQ obsažený v rovnici ZT se nazývá stupeň vazby. Jeho velikost je veličinou určující průběh křivek selektivnosti i fázových charakteristik obvodů. Rovnici křivek selektivnosti získáme výpočtem absolutní hodnoty vztahu pro ZT.

Křivky, které bychom získali, kdybychom do příslušných rovnic dosazovali za F konkrétní čísla ukazuje následující obrázek.

Jednotlivé průběhy platí pro určité konstantní velikosti stupně vazby kQ. Funkce tg má periodu 180 stupňů. Abychom mohli zakreslit fázovou charakteristiku, musíme způsobem nezávislým na předcházející rovnici určit ještě jeden bod, podle kterého zjistíme, která z period funkce tg je hledanou fázovou charakteristikou. Vhodným bodem je bod odpovídající nulovému rozladění F = 0, při kterém dostáváme z rovnice přenosové impedance v komplexním tvaru pro k je větší 0 fázový posun -90 stupňů. Proto se fázové charakteristiky pro kladné činitele vazby protínají při F = 0 v bodě -90 stupňů. Kdyby byl činitel záporný, celá soustava fázová charakteristika by se posunula tak, že by se křivky protínaly v bodě +90 stupňů. Stupně vazby kQ je menší 1  nazýváme vazbou podkritickou. Kritické vazbě odpovídá kQ = 1 a nadkritické kQ je větší 1.

Při podkritické a kritické vazbě mají křivky jen jeden vrchol. Při nadkritické vazbě se zmenšuje velikost přenosové impedance a na křivkách vznikají vrcholy dva. Je možné dokázat, že maximální hodnota přenosové impedance je pro všechny stupně vazeb, kromě vazby podkritické, stejná. Určíme ji z absolutní hodnoty přenosové impedance v rezonanci při kritické vazbě. Dosazení F=0 do rovnice křivek selektivnosti dostaneme rezonanční přenosovou impedanci vázaných obvodů.

Odtud získáme pro kritickou vazbu 

Jak plyne z rovnice ZT0, závisí velikost přenosové impedance dvojice vázaných obvodů značně na stupni vazby.  Zmenšení ZT0 proti ZTmax na stávající při nadkritické vazbě se nazývá prosedlání křivek b.

Pomocí prosedlání lze z naměřeného průběhu křivek vypočítat odpovídající stupeň vazby, neboť z definice b plyne.

Oba předcházející vztahy platí pro všechny typy vazeb.

Šířku pásma B dvojice vázaných obvodů určujeme zpravidla vzhledem k vrcholům křivek. Pro pokles impedance o 3 dB je možné položením

získat pro kritickou vazbu rozladění odpovídající okrajům pásma B3.

Postupem známým z teorie jednoduchých rezonančních obvodů dostaneme

z toho plyn, že dvojice vázaných obvodů má při kritické vazbě šířku pásma pro pokles přenosové impedance o 3 dB odmocnina ze 2 krát větší než je pásmo jednotlivých obvodů dvojice určené pro stejnou změnu impedance.

Šířky pásma pro ostatní případy se určují použitím generalizovaných křivek selektivnosti.