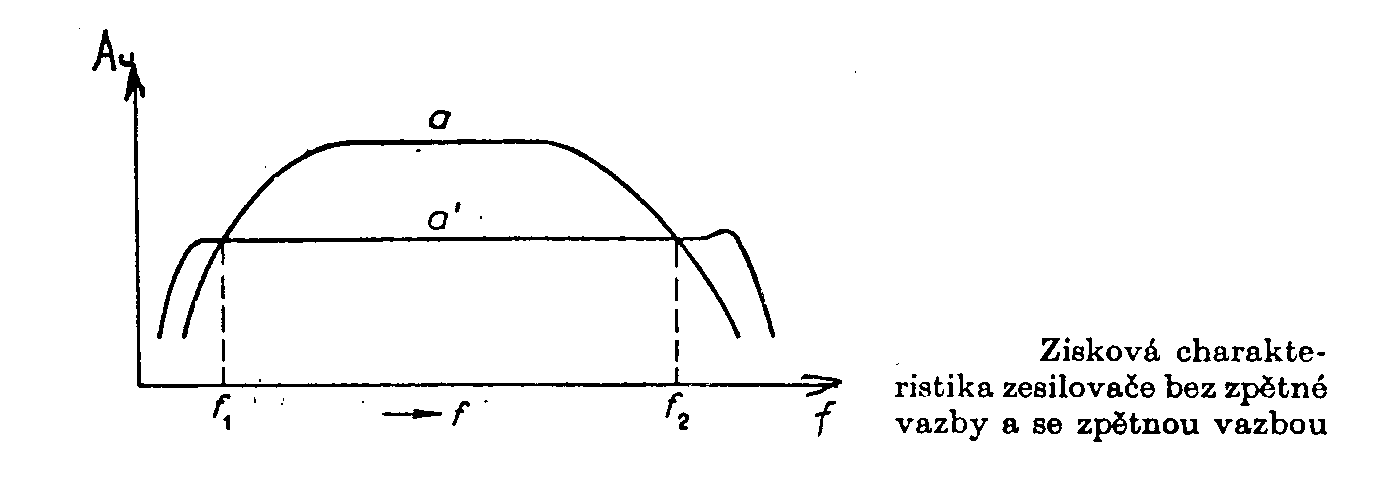|
|
HŘÍŠNÍCI NOVÝ UŽIVATEL nepřihlášený uživatel Právě si tyto stránky čte 1 člověk. |
|
Poslední změna:
29.09.2007 |
|
Návštěvník číslo: 26421 |
| ICQ:61783389 |
|
Copyright © 2003 Hell |
ElektronikaMaturitní otázkyZPĚTNÁ VAZBA U ZESILOVAČŮ23.Zpětná vazba u zesilovačů
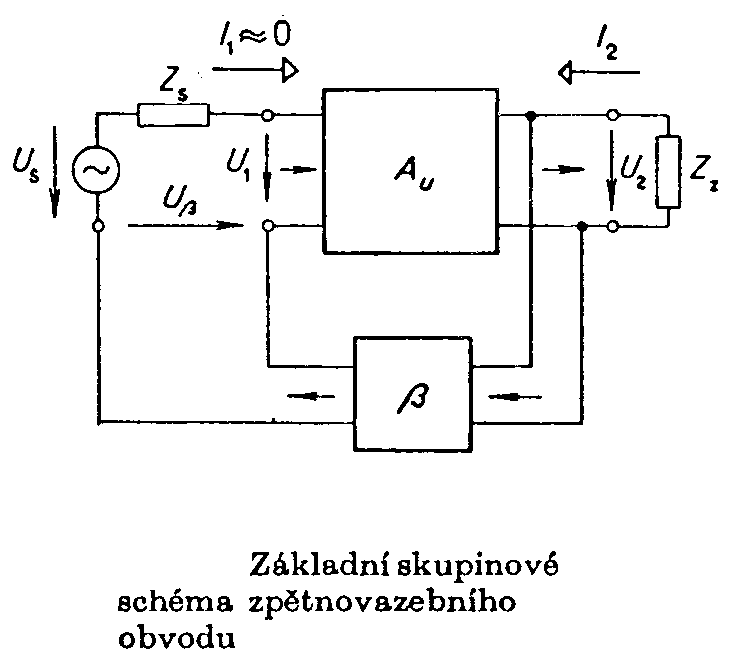
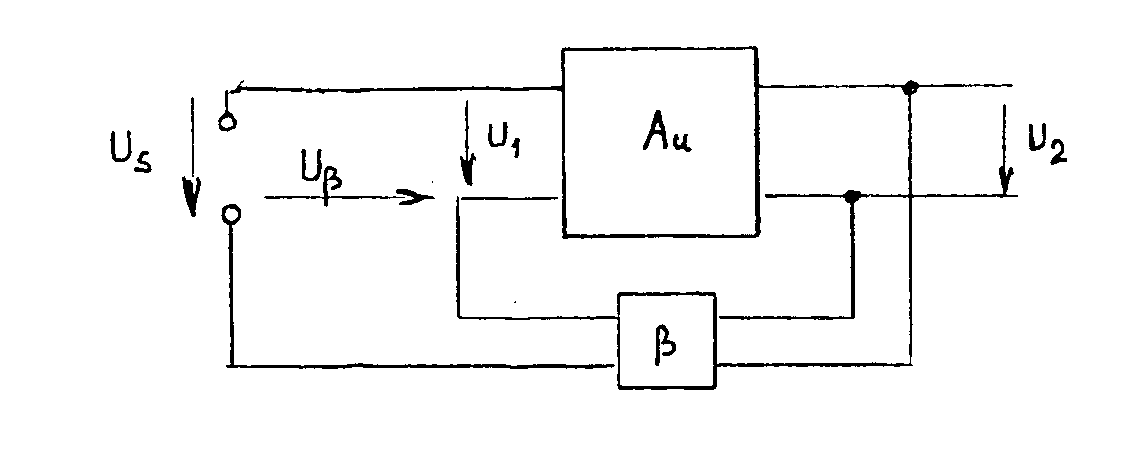
Zpětnou vazbou nazýváme zapojení, v němž je část výstupního napětí vedena buď přímo nebo přes určitý čtyřpól zpět na vstup a zde se algebraicky (s ohledem na znaménko) přičítá ke vstupnímu signálu. Základní schéma zapojení zpětnovazebního obvodu je uvedeno na obr. Základní zesilovací větev
má napěťové zesílení Z této rovnice plyne pro budící napětí
Us = U1 - Ub = U1(1-bA). Můžeme tedy napsat, že přenos zesilovače
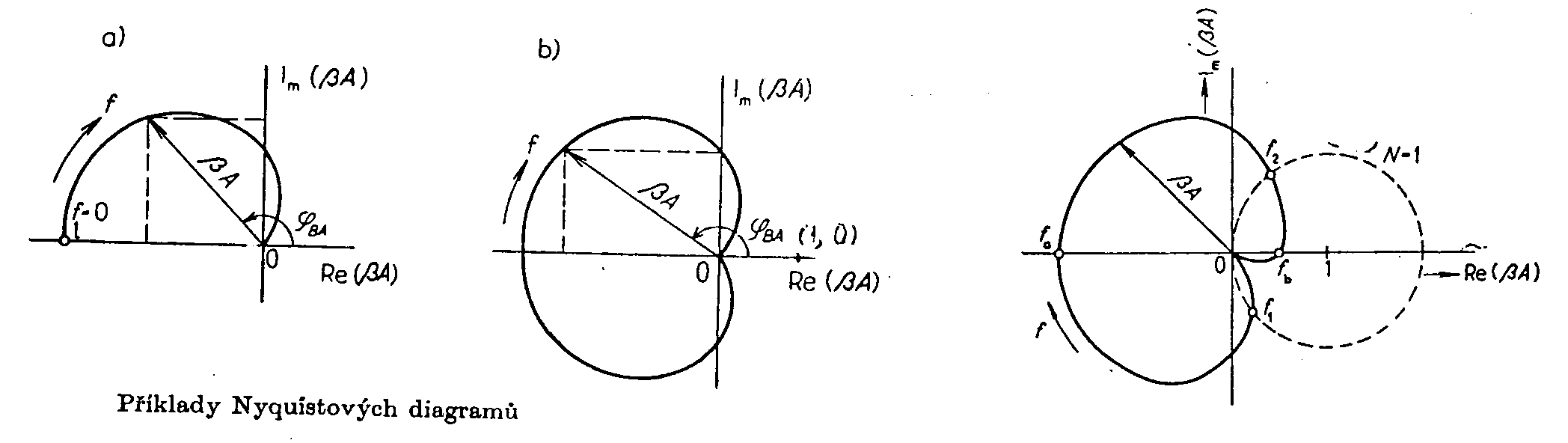
se zpětnou vazbou je dán vztahem Nyquistův diagramPouze v malém frekvenčním rozsahu a při nízkých frekvencích vykazují čtyřpóly čistě reálné zesílení. Obecně je vratný podíl komplexní číslo a jeho reálná i imaginární část jsou závislé na frekvenci. Můžeme tedy psát Na základě Nyquistova diagramu je založeno tzv. Nyquistovo kriterium stability zesilovačů, které patří do kategorie frekvenčních kriterií stability (oproti skupině algebraických kriterií). Velká výhoda těchto frekvenčních kriterií spočívá v tom, že je lze prakticky naměřit a v případě zjištění nestability nám umožní určit jaká opatření nutno udělat pro odstranění těchto nestabilit. Nyquistovo kriterium stability zní: Má-li být zesilovač stabilní, musí při procházení Nyquistova diagramu ve směru rostoucích frekvencí ležet vždy bod, o souřadnicích (1,j0) po levé ruce pozorovatele ( viz obr). Nakreslíme-li do komplexní roviny tedy kružnici
se středem v bodě (1,j0) a o poloměru r = 1, je pro všechny body Nyquistova
diagramu, které leží vně zmíněné kružnice zpětná vazba záporná a jsou splněny
podmínky pro stabilitu zesilovače a pro všechny body uvnitř této kružnice je
zpětná vazba kladná a jsou předpoklady pro vznik oscilací. Pro body Nyquistova
diagramu, které leží na kružnici (protínají kružnici) je zpětná vazba nulová,
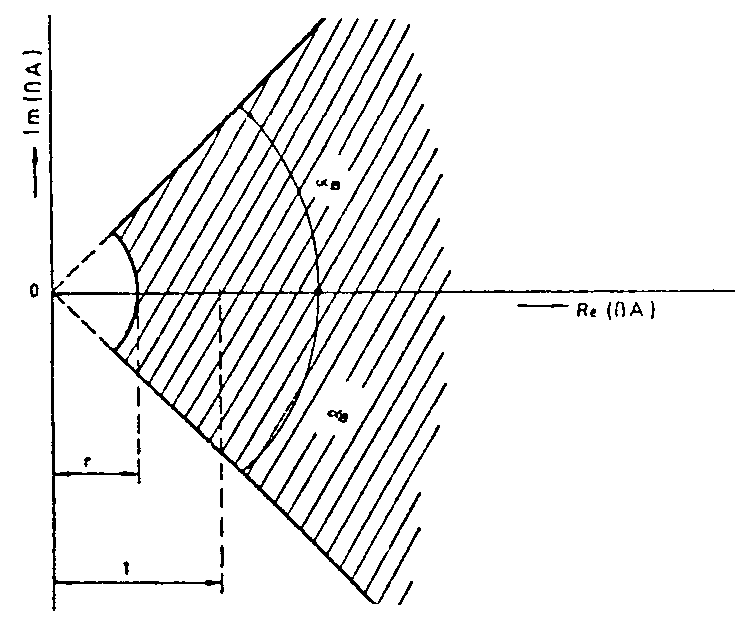
tzn. N = 1 a V praxi se musí počítat s určitou zálohou stability pro případ, že by se během provozu zesilovače měnil jeho zisk. Proto nemá Nyquistova charakteristika zasahovat do vyšrafované plochy, vymezené úhly aB = 10° a poloměrem r= 0,7 Čím větší je počet stupňů n, tím větší změny mohou v zesílení nastat. Proto se u vícestupňových zesilovačů požadují pro bezpečnostní úhel aB a poloměr r podmínky : aB ³ n.10°, r = 0,7n. Jednotkové kružnici, která je geometrickým
místem konců vektorů Vliv zpětných vazeb na přenosové vlastnosti zesilovače1) Vliv na napěťové zesílení: Napěťové zesílení je dáno
vztahem
2) Vliv na výstupní rušivá napět: Předpokládejme, že na výstupu se objeví napětí U2 = AU1 + Ur + Uh, kde Ur je rušivé napětí na výstupu zesilovače způsobené nedostatečnou filtrací, Uh je rušivé napětí na výstupu způsobené vlivem vyšších harmonických signálů ( nelineárním zkreslením budícího signálu). Napětí na vstupu je dáno součtem vnějšího budícího signálu Us a zpětnovazebního signálu Ub = bU2. Dosazením do výrazu pro výstupní napětí První člen rovnice představuje zesílení zesilovače se zpětnou vazbou pro užitečný signál. Druhý a třetí člen představuje příspěvek od rušivých signálů. Obě složky jsou zmenšeny vratným podílem N = 1 - bA. Záporná zpětná vazba potlačuje rušivé složky signálu, které mají původ uvnitř zesilovače, kladná zpětná vazba je zdůrazňuje. 3) Vliv zpětné vazby na frekvenční pásmo zesilovače: Frekvenční charakteristika zesilovače bez zpětné vazby a se zápornou zpětnou vazbou je znázorněna na obr. a … zesilovač bez zpětné vazby, a¢ … zesilovač se zpětnou vazbou Z grafu je zřejmé, že po zavedení záporné zpětné vazby, která zmenší zesílení zesilovače se dolní mezní kmitočet zmenší a horní mezní kmitočet vzroste. Při kladné zpětné vazbě je vliv opačný. Matematicky je vliv záporné zpětné vazby vyjádřen 4) Vliv na nelineární zkreslen:. Záporná zpětná vazba způsobí linearizaci převodních charakteristik, což způsobí i pokles amplitud vyšších harmonických a tím i zmenšení činitele harmonického zkreslení. 5) Vliv na vstupní a výstupní impedanci: Zde musíme rozeznávat paralelní (napěťovou) nebo sériovou (proudovou) zpětnou vazbu. Vliv zpětné vazby na impedanci lze určit podle tzv. Bodeova vzorce
Pro případ, že svorky, mezi nimiž se impedance určuje jsou spojeny nakrátko je bA(0). Jsou-li svorky, mezi nimiž se impedance určuje rozpojeny, je bA(¥). bA(0) = bA, jestliže se spojením uvažované dvojice svorek nakrátko zpětnovazební smyčka neovlivní bA = 0, jestliže spojení uvažované dvojice nakrátko způsobí zánik zpětné vazby. bA(¥) = bA, jestliže rozpojením obvodu mezi uvažovanou dvojicí svorek (t.j. zařazení nekonečně veliké impedance) se zpětná vazba neovlivní bA(¥) = 0, jestliže rozpojením obvodu mezi uvažovanou dvojicí svorek zpětná vazba zanikne. Pro napěťovou zpětnou vazbu platí bA(0) = 0, bA(¥) = bA. Pro proudovou zpětnou vazbu platí bA(0) = bA, bA(¥) = 0. Pro výstupní impedanci: při
napěťové zpětné vazbě je při
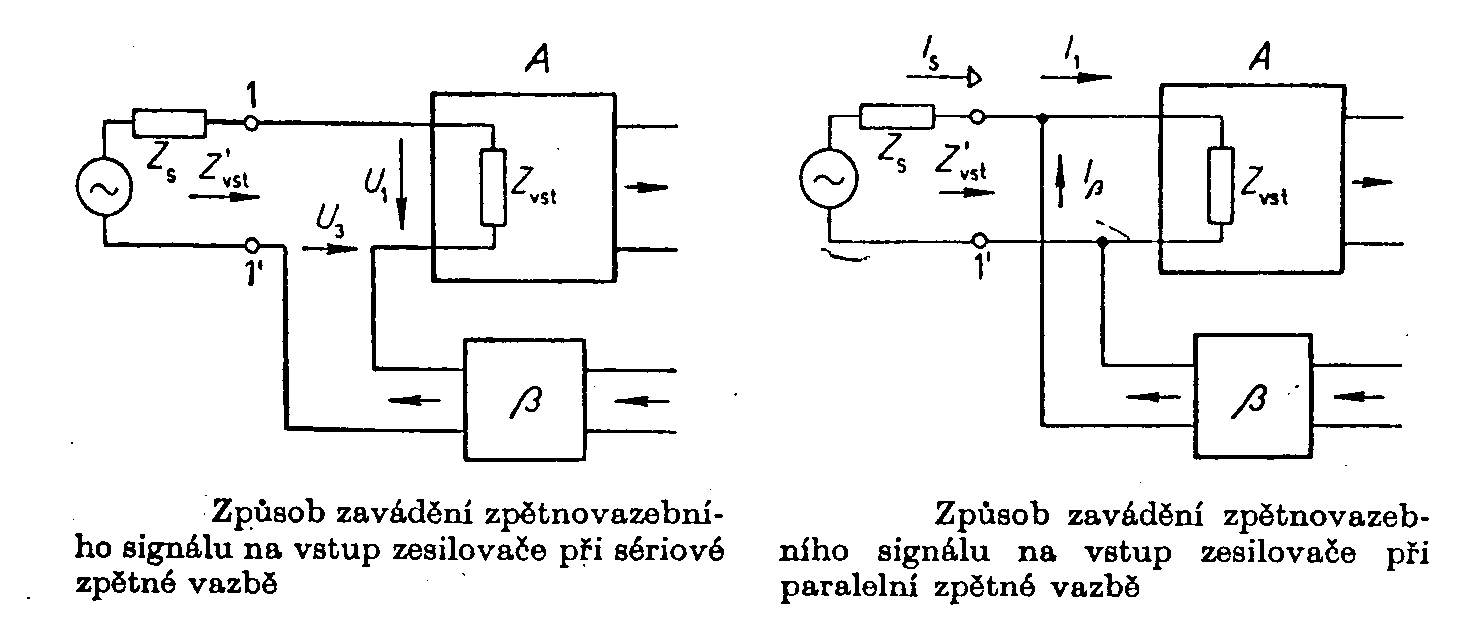
proudové zpětné vazbě je Máme-li tedy zesilovač s paralelní (napěťovou) zápornou zpětnou vazbou na výstupu a sériovou vazbou na vstupu, bude mít zesilovač malý výstupní odpor a velký vstupní odpor, což je v praxi nejžádanější případ. Jinak můžeme říci, že zesilovač s paralelní zpětnou vazbou na výstupu se chová jako zdroj konstantního napětí. Klesne-li zátěž, vzroste výstupní proud, tím klesne výstupní napětí a i část bU2, kterou přivádíme zpět na vstup zesilovače. Tím vzroste napětí U1 na vstupu, což vede k zvětšení výstupního napětí a tím ke kompenzaci poklesu napětí U2, který tento regulační proces vyvolal. Zesilovač se sériovou vazbou na výstupu se chová jako zdroj konstantního proudu. Vzroste-li výstupní proud tím, že poklesne zátěž, vzroste i část napětí bU2, tím se zmenší napětí U1 při konstantním napětí Us a poklesne i výstupní proud I2. Zesilovač se snaží udržet konstantní výstupní proud. Při sériové zpětné vazbě na zesilovače je bA(0)=bA a bA(¥)=0, takže je mezi svorkami 1 - 1¢ : a pro paralelní zpětnou vazbu na vstupu je bA(0) = 0 a bA(¥) = bA. Potom je vstupní impedance Často se používá smíšená zpětná vazba, t.j. současně působí napěťová i proudová zpětná vazba. Je-li A » 1 lze vzorec pro vratný podíl zjednodušit na tvar Zesílení takového zesilovače potom závisí pouze na činiteli zpětné vazby a ne na nestabilních prvcích vlastního zesilovače a tyto zesilovače jsou vhodné pro měřící a jiné náročné účely. |
|
zpět na předchozí stránku
Copyright © 2003 Hell
doporučené rozlišení 1024x768