|
|
HŘÍŠNÍCI NOVÝ UŽIVATEL nepřihlášený uživatel Právě si tyto stránky čte 1 člověk. |
|
Poslední změna:
29.09.2007 |
|
Návštěvník číslo: 26421 |
| ICQ:61783389 |
|
Copyright © 2003 Hell |
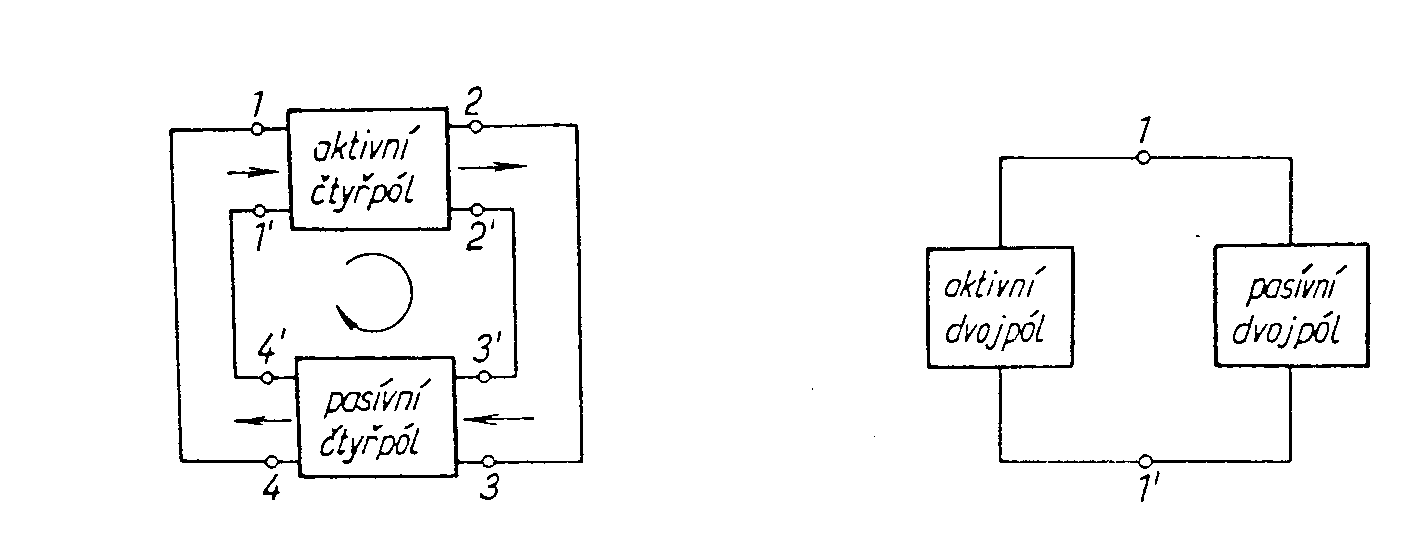
Elektornika II.Dokumenty a příkladyGenerátory sinusových průběhůVOŠ a SPŠE PLZEŇ, GENERÁTORY NESINUSOVÝCH PRŮBĚHŮ, Učební texty Generátory sinusových průběhů. Generátory sinusových průběhů dělíme do dvou skupin: - generátory zpětnovazební - generátory jednobranné Zpětnovazební generátory můžeme rozdělit na : - LC oscilátory - RC oscilátory Zpětnovazební oscilátory se skládají z aktivní větve, která obsahuje aktivní čtyřpól a ze zpětnovazební větve, která obsahuje pasivní čtyřpól, nazývaný řídící člen. Jednobranné oscilátory se skládají z aktivního čtyřpólu, který je paralelně spojen s pasivním čtyřpólem. Aktivní čtyřpól má v určité oblasti záporný dynamický odpor a za určitých podmínek může tato soustava kmitat netlumenými harmonickými kmity. Pasivním čtyřpólem je vždy obvod LC (není znám takový obvod RC, který by v této sestavě mohl vytvořit oscilátor. Bloková schemata obou typů oscilátorů jsou uvedena na obr. Zpětnovazební oscilátory. Skládají se z přímé větve, obsahující aktivní zesilovací člen se zesilovacím činitelem A a zpětnovazebním členem, jehož přenos je b. Zesílení celého obvodu se zapojenou zpětnou vazbou je b je přenos zpětnovazebního členu. Všechny tři členy mají obecně komplexní, na frekvenci závislý charakter a podmínka pro vznik oscilací je: jb je fázový posuv zpětné větve Tím dostáváme t.zv. amplitudovou a fázovou podmínku pro vznik oscilací. Pro realizaci oscilátorů musí být pro nastartování
kmitů Kmitočtové závislosti amplitudové a fázové podmínky
oscilací, bA(f) a j(f)
závisí na amplitudových a fázových charakteristikách obou čtyřpólů. Lze dosáhnout
takových průběhů těchto závislostí, že pro daný kmitočet f0 jsou
splněny obě podmínky oscilací a pro jiný kmitočet není aspoň splněna podmínka
fázová. Fázový posun napětí zpětnovazební smyčky se mění obvykle s kmitočtem
mnohem rychleji, než jeho amplituda. Proto o stabilitě kmitočtu oscilací rozhoduje
především průběh fázové zpětnovazební charakteristiky oscilátoru j(f).
Zpětnovazební čtyřpól se musí navrhnout tak, aby strmost jeho fázové charakteristiky
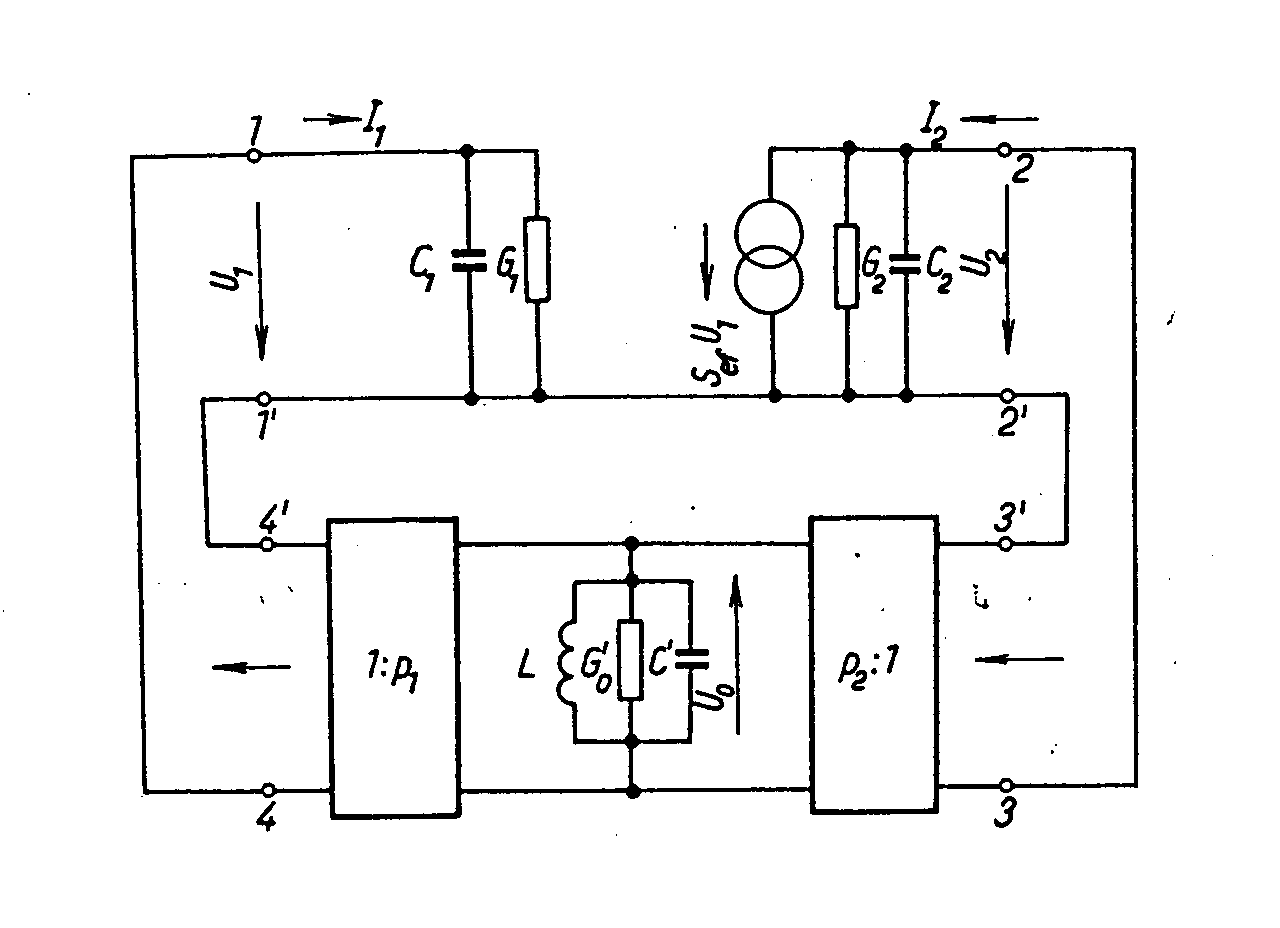
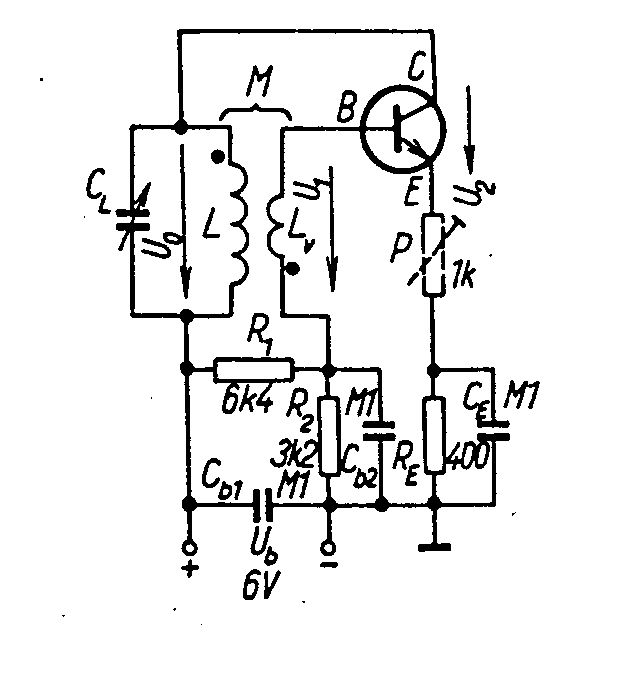
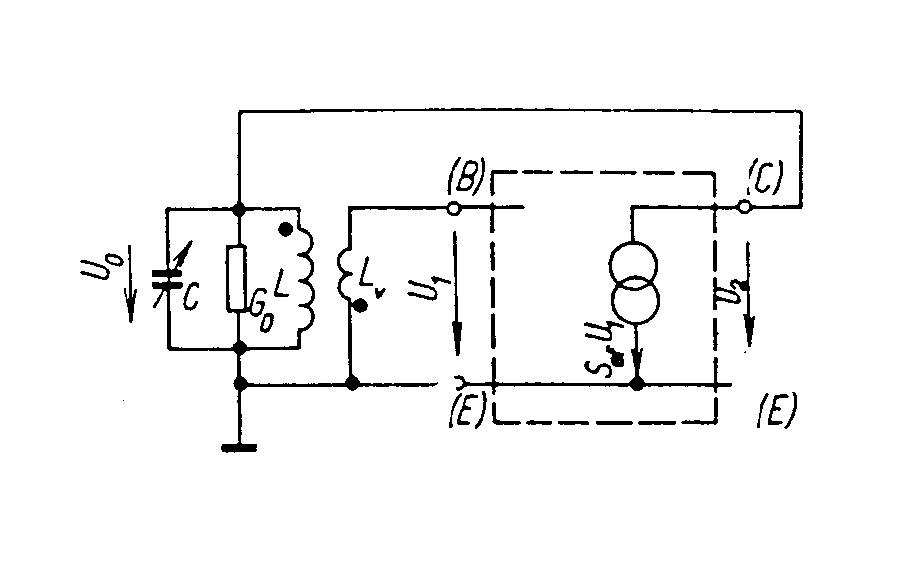
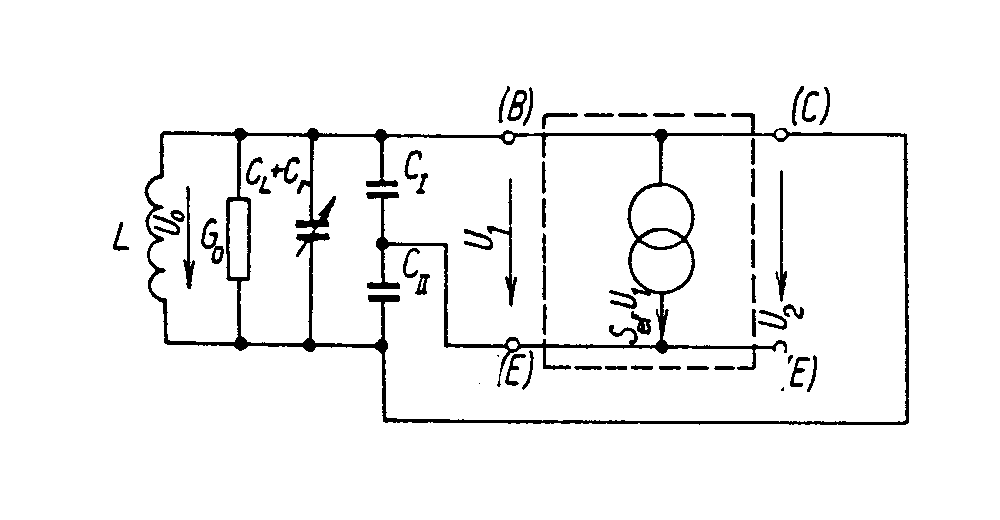
v okolí oscilačního kmitočtu Podle druhu řídícího členu známe zpětnovazební oscilátory: - LC - řídícím členem je vhodně upravený rezonanční obvod LC. Používají se pro vyšší frekvenční pásma od 100kHz do stovek MHz. - krystalové oscilátory - používají jako řídící člen mechanický rezonátor, nejčastěji krystalový výbrus piezoelektrických materiálů, které se vyznačují vysokou kmitočtovou stabilitou generovaných kmitů. - RC oscilátory - řídící člen je sestaven z vhodných odporů R a kondenzátorů C. Zpětnovazební LC oscilátory. Základní zapojení oscilátoru je blokově uvedeno na obr. Aktivní prvek je zde znázorněn zdrojem proudu velikosti Sef.U1, paralelně zapojených s výstupní vodivostí G2 a C2. Vstup je reprezentován vstupní vodivostí G1, C1. Sef je strmost aktivního prvku (t.j.
závislost výstupního proudu i2 na vstupním řídícím mapětí u1,
čili 1. harmonické a s amplitudami napětí U1, resp. U2. Efektivní strmost, která charakterizuje zesilovací stupeň v nelineárním provozu závisí na použitém tranzistoru, na pracovním kmitočtu, na poloze pracovního bodu a na vstupním napětí. Čím je vstupní napětí větší, tím je efektivní strmost menší. Určuje se buď výpočtem nebo měřením. Z náhradního schematu je patrné, že rezonanční kmitočet oscilátoru závisí nejen na parametrech vlastního rezonančního obvodu LC’, ale také na vstupní a výstupní kapacitě aktivního čtyřpólu. Rezonanční dynamická vodivost vlastního řídícího
členu je Stejně se ovlivní i činitel jakosti rezonančního obvodu Q’. Toto ovlivnění se nejlépe vyjádří, převedeme-li obě složky vstupní a výstupní impedance přes transformační členy na řídící obvod LC’. Podle známých transformačních vztahů platí Potom výsledná rezonanční vodivost je dána a výsledná kapacita řídícího obvodu je Fázová podmínka j = 2kp může být splněna pouze pro rezonanční kmitočet výsledného řídícího obvodu. T.zn. Amplitudová podmínka oscilací je Napětí na výstupu zesilovacího stupně při obecné zatěžovací impedanci je Zatěžovací vodivost Gz najdeme tak, že převedeme všechny vodivosti na výstupní svorky zesilovače Takže výsledná amplitudová podmínka je Tato amplitudová podmínka obsahuje rovněž konkrétní parametry obvodu. Pouze členy p1 a p2 mají stále obecnou povahu a určují vlastnosti transformačních členů, kterými je řídící člen upraven do tvaru čtyřpólu. Kmitočtová a amplitudová podmínka je dána dvěma rovnicemi, které obsahují celkem 11 parametrů oscilátoru. Z nich je 9 daných nebo vhodně určených a zbylé dvě vypočítáme. V mnoha případech lze uvedené vztahy zjednodušit.
Tak např. čím jsou napěťové převody transformačních členů větší, tím je vliv
nahodilých kapacit zesilovacího stupně na řídící obvod menší a tím více můžeme
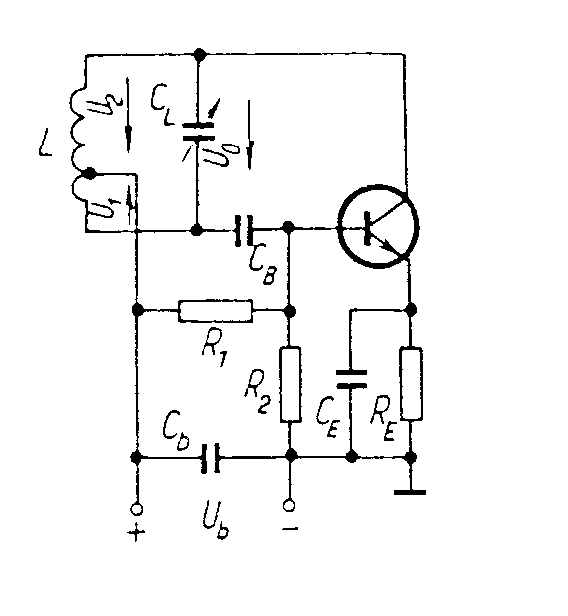
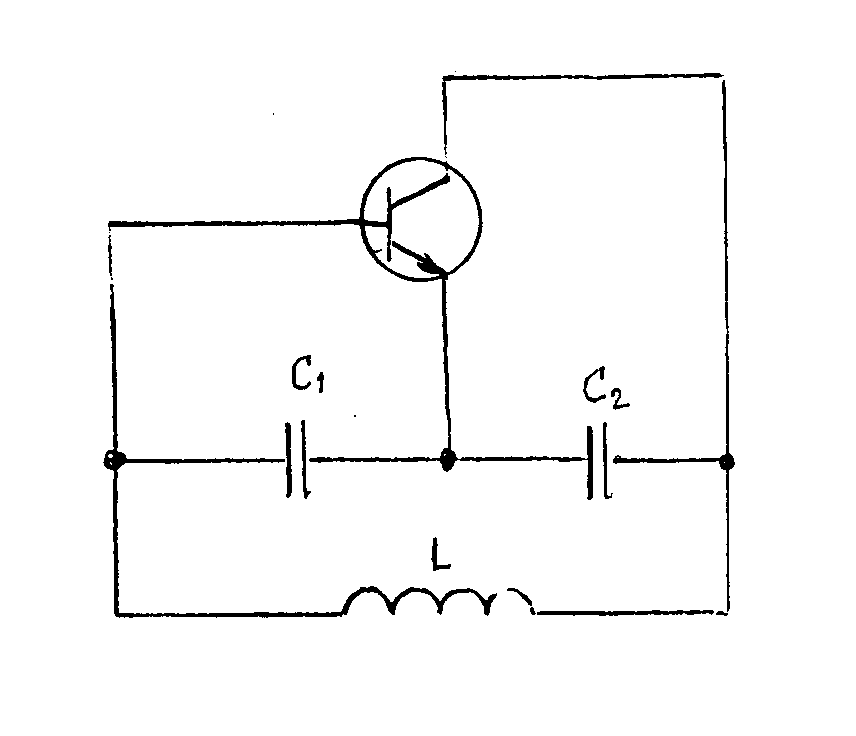
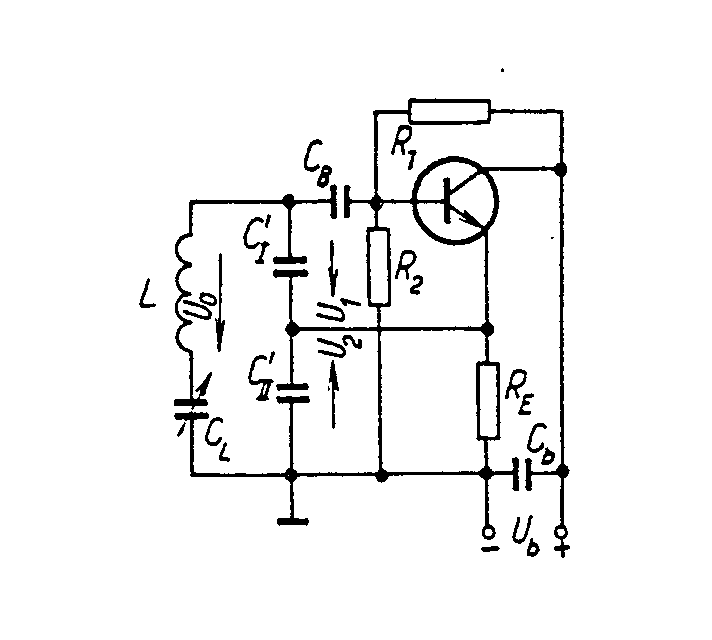
předpokládat, že Je zřejmé, že jeden z převodů musí být kladný, druhý záporný, aby byla splněna amplitudová podmínka. Například pro rezonanční vodivost řídícího obvodu G´0=20mS a efektivní strmost zesilovacího stupně Sef = 6mA/V, platí Existuje velké množství dvojic p1 a p2, jejichž součin je -300. Doplňme požadavek, aby výstupní napětí bylo 3x větší než vstupní a aby výstupní napětí bylo ve fázi s napětím řídícím. Potom: p2 > 0 a p1=-30, p2=10. Zapojení zpětnovazebních LC oscilátorů. V praxi rozdělujeme LC oscilátory na oscilátory s indukční vazbou a oscilátory v tříbodovém zapojení. Oscilátory s indukční vazbou se vyznačují tím, že řídící člen LC má se zesilovačem indukčně vázanou pouze jednu stranu. Základní zapojení je uvedeno na obr. Zapojení oscilátoru Náhradní schéma Transformují-li se vnitřní admitance zesilovacího stupně do řídícího obvodu, získáme náhradní schéma, jak je uvedeno na obrázku. Převod p2, který se uplatňuje mezi rezonančním obvodem a výstupem zesilovacího stupně, udává poměr U0/U2. Protože ale je výstupní obvod připojen přímo k rezonančnímu obvodu, je zřejmě U0 = U2 a tudíž p2 = 1. Převod mezi rezonančním obvodem a vstupem zesilovacího stupně je p1 = U0/U1 musí být podle amplitudové podmínky záporný. To se snadno dosáhne správným zapojením konců indukčnosti L a vazební cívky Lv. Napětí U1 a U0 jsou v protifázi, takže jejich poměr, který udává převod p1 je záporný. Protéká-li řídícím členem při rezonanci cirkulační proud I, je napětí na rezonančním obvodu U0 = jw0LI a napětí indukované na vazební cívce, které závisí na vazební indukčnosti, je U1=-jw0MI. Z toho plyne závislost transformačního poměru Dosazením do obecného vztahu pro amplitudovou a kmitočtovou podmínku, dostaneme a Opět pro oscilátory s velmi velkým vstupním odporem (s unipolárními tranzistory nebo elektronkové) platí Oscilátor tohoto typu se nazývá Reinartzův. Je možná i druhá varianta, že v kolektorovém obvodu tranzistoru je pouze cívka a rezonanční obvod je v obvodu báze. Oscilátor tohoto typu se nazývá Snellův. Oscilátory v tříbodovém zapojení. Tříbodové oscilátory mají připojen aktivní prvek k rezonančnímu obvodu ve třech bodech. Buď se provede cívka s odbočkou a k ní se připojí tranzistor (Hartleyův oscilátor), nebo se provede kapacitní větev rezonančního obvodu jako kapacitní dělič a k němu se tranzistor připojí (Colpittsův oscilátor). Hartleyův oscilátor. U Hartleyova oscilátoru je cívka řídícího obvodu LC rozdělena do dvou sekcí, k nimž je připojen vstupní, resp. výstupní obvod zesilovacího stupně. Schema zapojení je uvedeno na obr. Ideové schéma Schéma zapojení Označíme-li indukčnost celé cívky L, indukčnosti jednotlivých částí L1 a L2 a vzájemnou indukčnost mezi sekcemi M, jsou převody řídícího čtyřpólu dány vztahy Převod p1 je zřejmě záporný, protože napětí U0 a U1 jsou v protifázi. Je-li vazba mezi sekcemi indukčnosti řídícího obvodu těsná, jsou s dostatečnou přesností dány převody poměrem odpovídajících počtů závitů Dosazením těchto vztahů do obecné kmitočtové a amplitudové podmínky oscilací se získá dvojice rovnic pro návrh oscilátorů v Hartleyově zapojení. Colpittsův oscilátor. Colpittsův oscilátor má upravenou kapacitní větev řídícího členu tak, aby bylo možno k ní připojit zesilovač ve třech bodech. Schéma zapojení je uvedeno na obr. Ideové schéma Pro střídavé napětí je zde uzemněna báze tranzistoru. To je výhodné, protože emitorový odpor RE se řadí paralelně k malému vstupnímu odporu tranzistoru a nepřispívá k tlumení řídícího rezonančního obvodu. Požadujeme-li přeladitelnost v určitém rozsahu, připojujeme ladící kondenzátor paralelně k indukčnosti řídícího obvodu. Vlastní kapacita rezonančního obvodu Colpittsova oscilátoru je (je-li použit) Cr je rozptylová kapacity cívky a spojů Vstupní a výstupní kapacity tranzistoru se řadí paralelně ke kapacitám děliče, takže skutečné provozní kapacity děliče jsou Proto také celková provozní kapacita řídícího rezonančního obvodu je takže kmitočtová podmínka oscilací Colpittsova oscilátoru je Náhradní schéma Colpittsova oscilátoru pro střídavá napětí je na obr. Vstupní napětí U1 se odebírá z kapacity CI a po zesílení je vedeno napětí U2 na kapacitu CII. Kolektor je připojen k opačnému konci rezonančního obvodu, než ke kterému je připojena báze. Tím je splněna oscilační podmínka, aby jeden z převodů byl záporný. Podle naznačené polarity je zřejmě záporný převod p1 Naopak převod p2 je kladný. takže amplitudová podmínka má tvar Colpittsův oscilátor lze použít s obvody se soustředěnými parametry (klasický řídící obvod typu LC) až do frekvencí asi 100 MHz. Nahradí-li se řídící obvod obvodem s rozloženými parametry (např. vhodným úsekem vysokofrekvenčního vedení nakrátko o délce l = l/4) lze použít tento typ oscilátoru až do kmitočtu stovek MHz. Příklad návrhu Colpitsova oscilátoru. Navrhnout Colpittsův oscilátor přeladitelný otočným kondenzátorem, s počáteční kapacitou CLp = 13pF v kmitočtovém pásmu f0 = 3,5 - 4MHz. Cívka pro řídící obvod má indukčnost L = 5mH a v celém pracovním pásmu má stálý činitel jakosti Q´ = 100. Počet závitů cívky N = 20. Rozptylové kapacity odhadneme na Cr = 10pF. Dolaďovací trimr má kapacitu Cd = 15±10pF. Vybraný tranzistor má v pracovním bodě v požadovaném kmitočtovém pásmu při amplitudě vstupního napětí U1 = 0,1V vstupní vodivost G1 = 10mS, vstupní kapacitu C1 = 500pF, výstupní vodivost G2 = 50mS, výstupní kapacitu 68pF a efektivní strmost Sef = 5mA/V. Chceme odebírat výstupní napětí U2 = 2V. Řešení. V zadání jsou uvedeny všechny veličiny, které jsou v amplitudové podmínce, až na kapacity CI a CII. Rezonanční admitance je Z amplitudové podmínky nyní vypočítáme potřebný poměr kapacit děliče CII/CI Dosadíme-li za CII/CI = x, dostaneme
Dosadíme-li číselné hodnoty daných parametrů, dostaneme po úpravě 101x2 - 48,2x +1,41 = 0 Řešením tého kvadratické rovnice dostaneme kořeny x1 = 0,447, x2 = 0,0312 Amplitudové oscilační podmínce vyhovují dvě řešení a bude nutno vybrat to výhodnější. Veličina x dává vlastně přenos pasivního řídícího členu: Při amplitudě vstupního napětí U1 = 0,1V odpovídají pro výpočet, který jsme provedli dvě hodnoty výstupního napětí: Je zřejmé, že z hlediska požadavku na hodnotu výstupního napětí se první kořen nehodí. Při volbě druhého řešení bude napětí na kolektoru tranzistoru dostatečně velké, abychom dostali požadované U2 = 2V. Navíc při volbě x = 0,0312 bude volnější vazba řídícího obvodu LC, což přispěje k větší stabilitě kmitočtu oscilátoru. Zatím známe pouze poměr obou kapacit. Hodnoty jednotlivých kapacit určíme z kmitočtové podmínky oscilátoru. Při dané indukčnosti cívky musí mít obvod minimální celkovou kapacitu Pozn. Uvedený vzorec vyplyne ze základního Thomsonova vzorce pro rezonanční kmitočet obvodu, budeme-li dosazovat frekvenci v MHz a indukčnost v mH. Kapacita vyjde v pF. Minimální celková kapacita je tedy dána Odtud dostaneme Po úpravě Tím jsme dostali celkové kapacity CI a CII. Nyní musíme ještě vypočítat, jaké kapacity musíme vletovat do obvodu, abychom dostali výsledné vypočítané celkové kapacity. Aby přesáhl oscilátor požadované kmitočtové pásmo, musí se měnit kapacita řídícího obvodu o Ladící kondenzátor, u něhož jsme předpokládali počáteční kapacitu CLp=13pF musí mít konečnou kapacitu CLk = CLp+DC = 13+45 = 58pF K určení provozního činitele jakosti musíme nejdříve znát transformační převody. Rezonanční admitance řídícího obvodu je Zatěžovací admitance kolektorového obvodu tranzistoru je Zatěžovací odpor v kolektorovém obvodu je Provozní činitel jakosti je Na cívce řídícího obvodu bude střídavé napětí s amplitudou U0 = U1 + U2 = 0,1 + 3,21 = 3,31V Požadované výstupní napětí U2 = 2V dostaneme
tedy na odbočce cívky, která bude mít Stabilita LC oscilátorů. Stálost oscilátorů vyjadřujeme relativní změnou frekvence Df/f0. Oscilátory LC dosahují dlouhodobé stability nejvýše 10-3, což znamená, že u oscilátoru s frekvencí f0 = 1MHz musíme počítat s dlouhodobou nestabilitou 1 kHz. Náhodné změny kmitočtu jsou dány: - mechanickými změnami na ladícím obvodu oscilátoru - změnami teploty okolí na ladící prvky oscilátoru - změnami vlastností použitého tranzistoru (nebo elektronky), způsobenými stárnutím, výměnou součástek, změnami napájecích napětí a pod. Největší vliv ze všech jmenovaných mají změny vstupních a výstupních kapacit zesilovacího stupně. Z obecné kmitočtové podmínky vyplývá, že potlačení
tohoto vlivu bude tím větší, čím větší budou převody transformačních členů p1
a p2. Derivováním obecné kmitočtové podmínky a úpravou získaného
vztahu, budeme-li předpokládat zjednodušení, že Sef/f0
@ p1p2, dále
vyjádřením převodů pomocí jejich geometrického průměru Z uvedené rovnice je vidět, že nežádoucí změny kmitočtu jsou malé, jsou-li splněny podmínky: - řídící obvod LC má velký činitel jakosti Q - tranzistor pracuje s vysokou strmostí Sef - zesilovací stupeň vykazuje malé nahodilé změny DC1 a DC2 - čím bude menší pracovní kmitočet oscilátoru w0. Jsou-li předpokládané změny kapacit DC1
a DC2 stejné, je vhodné volit k = 1. Je-li obecně DC1
= m.DC2, je při jinak stejných podmínkách poměrná
odchylka kmitočtu nejmenší, nastaví-li se převody tak, aby
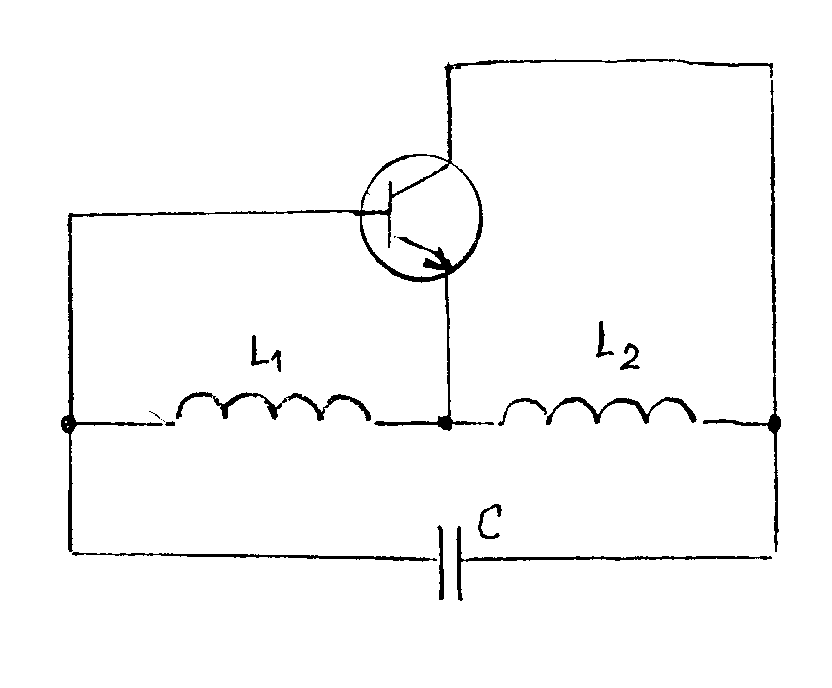
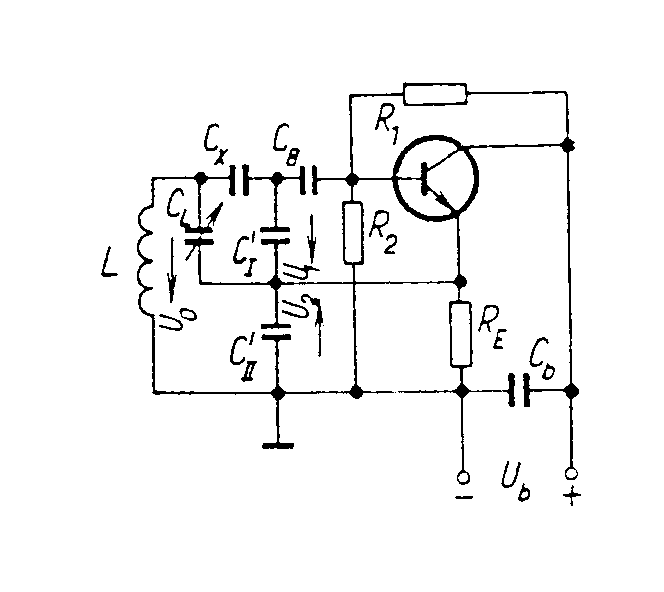
Oscilátory s větší stálostí kmitočtu. Tato zapojení se odvozují převážně od Colpittsova zapojení. Nejznámější je t.zv. Clappovo zapojení, uvedené na obr. Kapacitní větev je složena ze tří kondenzátorů,
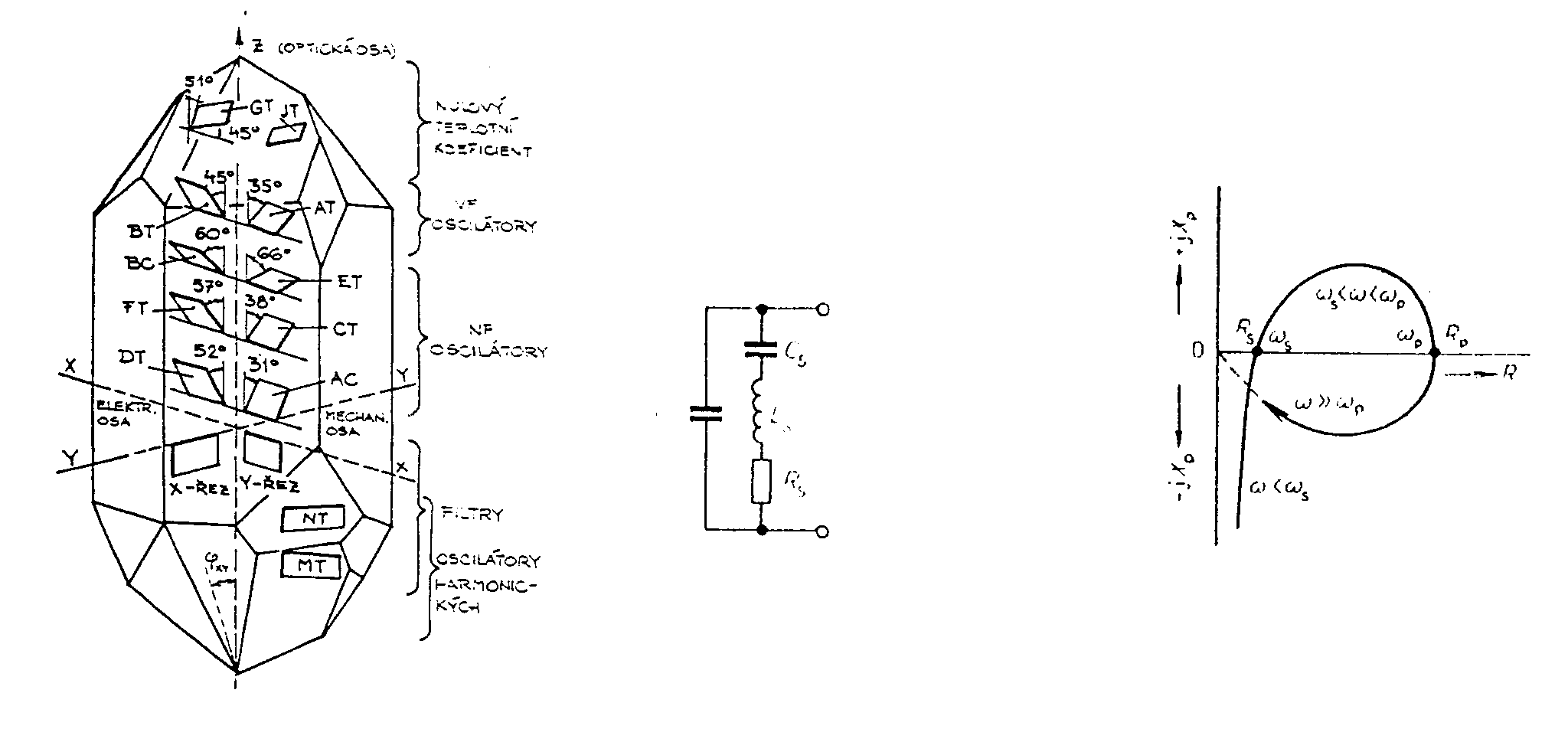
zapojených v serii. Převody jsou dány vztahy Dobrá kmitočtová stabilita je, jsou-li převody p1 a p2 co největší. Potom se celková ladící kapacita řídícího obvodu téměř rovná kapacitě ladícího kondenzátoru C@CL. Clappův oscilátor může dosáhnout dlouhodobou stabilitu až 10-5. Nevýhodou Clappova oscilátoru je, že při přelaďování směrem k vyšším kmitočtům (t.j. při zmenšování ladící kapacity CL se zvětšují převody p1 a p2) se rychle zvětšují požadavky na efektivní strmost Sef a tím klesá amplituda kmitů. Proto se používá Clappův oscilátor při přelaďování pouze v poměru krajních frekvencí 1:1,2. Jiné zapojení oscilátoru s větší stabilitou je t.zv. Vačkářův oscilátor. Tento je rovněž odvozen z Colpittsova oscilátoru a jeho schéma zapojení je na obr. Toto zapojení umožní přelaďování v rozsahu 2,5 : 1 aniž se při tom mění amplituda oscilací. Je to dáno zapojením kapacitní větve řídícího obvodu. Kapacity musí vyhovovat vztahům Cx « CI a Cx « CII. Dále je kapacita ladícího kondenzátoru CL » Cx. Potom je celková kapacita řídícího obvodu rovna a transformační převody Oscilační podmínky jsou dány vztahy Velmi dobrou stabilitu mají rovněž oscilátory s unipolárními tranzistory. Potřebujeme-li odebírat z oscilátoru nějaký výkon, musíme počítat s výrazným vlivem zatěžovací impedance na stabilitu oscilátoru. Proto se tento vliv musí co nejvíce omezit. Buď se použijí vhodné oddělovací kondenzátory nebo se odebírá napětí buď z odbočky řídícího obvodu nebo se navíjí přídavné vinutí k oddělení zátěže a k odběru signálu. Oscilátory řízené krystalem. K zvětšení frekvenční stability oscilátorů bylo ukázáno, že je nutno používat řídící obvod s co největším činitelem jakosti Q. Největší technicky dosažitelný činitel jakosti nalézáme u krystalových piezoelektrických rezonátorů. Jejich rezonanční kmitočet je určen hmotností, pružností a způsobem kmitání destičky nebo tyčinky, vybroušené z monokrystalu, nejčastěji křemene nebo turmalínu (borokřemičitan hlinito-hořečnato-vápenato sodný - tento patří mezi drahé kameny a je drahý). Tyto látky krystalizují v šesterečné struktuře, t.zn. že řezy kolmé na podélnou osu mají tvar pravidelných šestihranů. Monokrystaly těchto látek mají tři osy - optickou, označovanou Z, která je totožná s podélnou osou krystalu, elektrickou - označovanou X (procházející přes vrcholy šestiúhelníkového řezu) a mechanickou, označovanou Y (procházející středem hran šestiúhelníka). Z monokrystalu se řežou destičky, které se opatřují napařenými nebo přiloženými elektrodami. Na orientaci řezů vůči osám závisí vlastnosti krystalu. Typické řezy krystalu jsou uvedené na obr. Typické řezy výbrusů el.náhradní schema průběh impedance Křemený krystalový výbrus se chová jako elektrický rezonanční obvod, schopný seriové i paralelní rezonance s činitelem jakosti Q = 104 - 107. Seriový odpor rezonančního obvodu je velmi malý a při odvozování rezonanční frekvence ho můžeme zanedbat. C0 je statická kapacita rezonátoru, vyjadřuje pouze kapacitu elektrod a závisí na tvaru a na uspořádání rezonátoru. Je nezávislá na mechanických vlastnostech rezonátoru. Potom pro impedanci lze napsat rovnici úpravou dostaneme Z rovnice lze určit dvě rezonanční frekvence: 1) pro Z = 0, je 2) pro Z = ¥,
je Vidíme, že zatím co seriová rezonance je nezávislá na neurčité kapacitě C0, je na ní paralelní rezonance závislá. Z obou vztahů je zřejmé, že seriová rezonance je vždy nižší, než paralelní. Rozdíl těchto frekvencí bývá ovšem velmi malý, protože dynamická kapacita C bývá o několik řádů menší než C0. Z průběhu závislosti Z = f(w) je patrné, že krystal má kapacitní charakter v celém rozsahu frekvencí, vyjma intervalu < ws ¸ wp >, kde má induktivní charakter. S tím souvisí i způsoby změny rezonančního ws a paralelního wp kmitočtu vně připojenými reaktancemi, jak je znázorněno na obr. Možnosti posunutí seriového a paralelního kmitočtu krystalu.
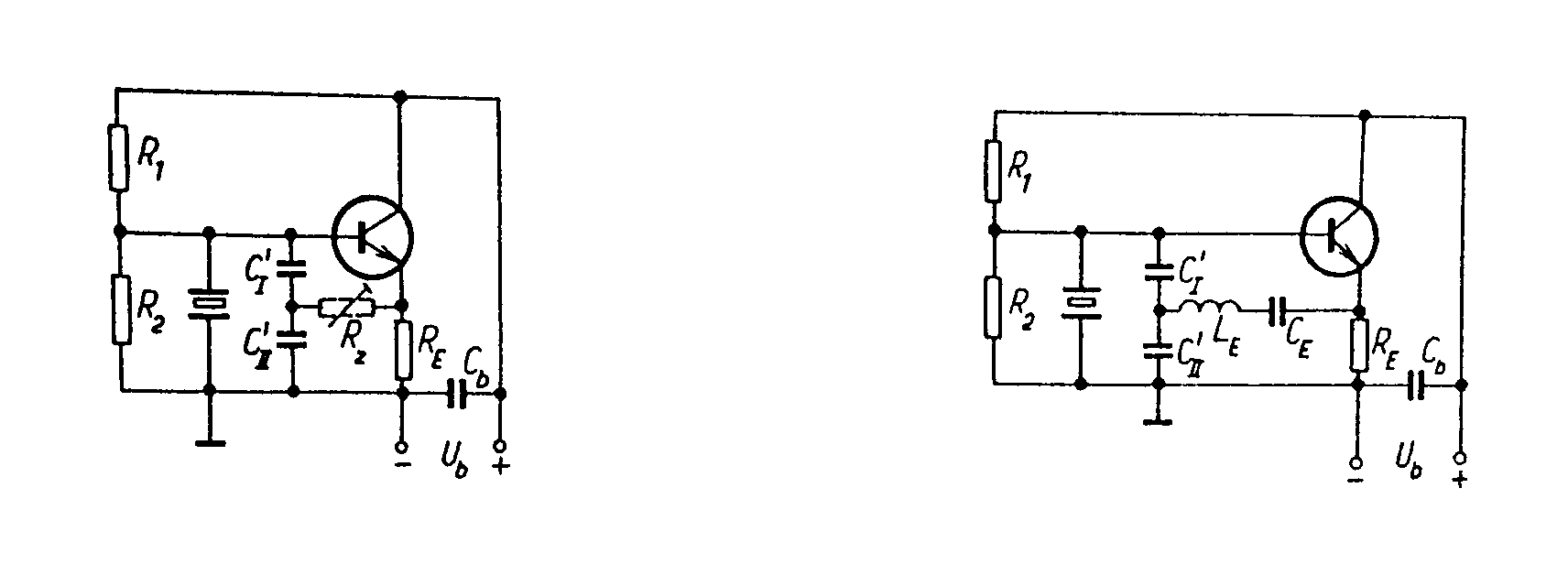
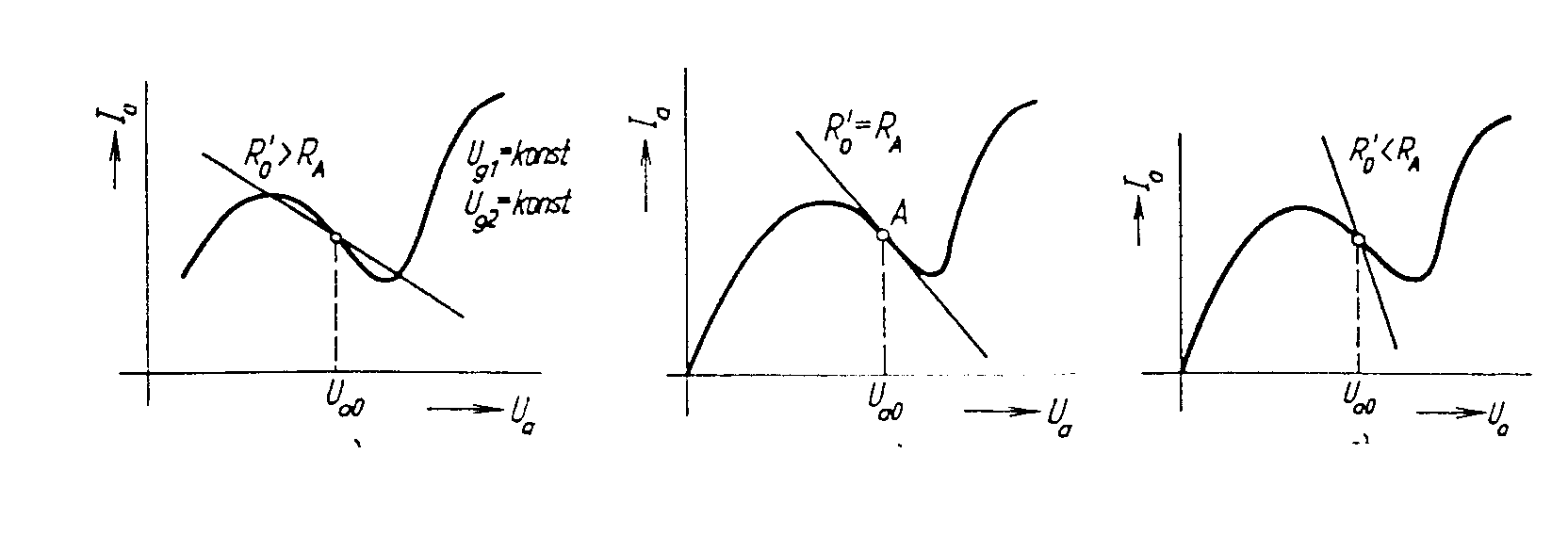
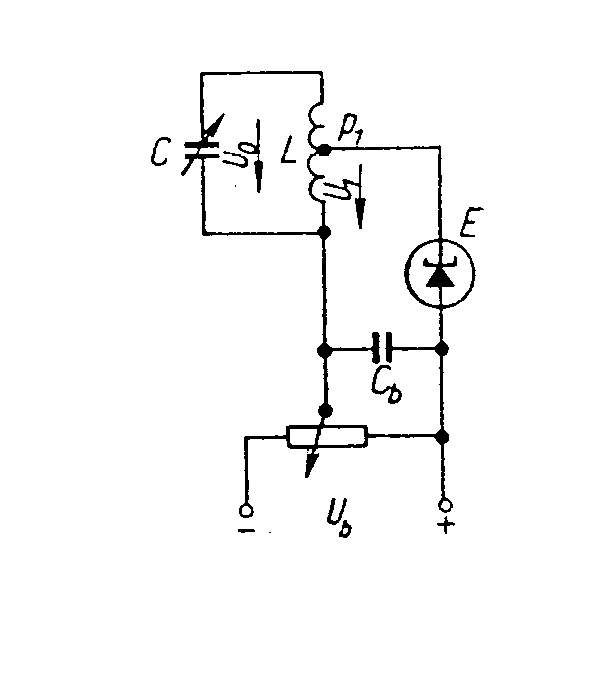
Seriový kmitočet lze posouvat jen seriově řazenými reaktancemi Ls a Cs a paralelní kmitočet paralelně řazenými reaktancemi Lp a Cp. Směr posunutí kmitočtu je naznačen šipkami a ¯. Zapojení krystalových oscilátorů bývá nejčastěji odvozováno od Colpittsova zapojení. Nejznámější je t.zv. Pierceovo zapojení. Pierceovo zapojení Zapojení oscilátoru „Tritet² Kmitočet těchto oscilátorů je mezi seriovým a paralelním kmitočtem rezonátoru. Čím větší jsou kapacity kondenzátorů CI a CII, tím je větší skutečná statická kapacita krystalového rezonátoru a tím více se kmitočet oscilací blíží k seriovému. Je vhodné, aby kapacity kondenzátorů CI a CII byly co největší, protože tím přesněji se dosáhne definovaný kmitočet oscilací f0 = fs. Navíc při velkých hodnotách CI a CII dosáhneme lepší kmitočtové stability oscilací. Pro nastavení podmínky oscilací se používá odporový trimr Rz, kterým se zmenší efektivní strmost aktivního prvku na potřebnou velikost. U oscilátorů, které mají málo potlačené parazitní rezonance se používá zapojení Tritet, které se liší od Pierceova nahrazením odporu Rz seriovým rezonančním obvodem LECE, naladěným na rezonanční kmitočet f0. Pro jiný kmitočet než f0 je impedance obvodu LECE komplexní a mnohem větší, takže na jiném kmitočtu oscilace nevzniknou. Jednobranné oscilátory. Tyto oscilátory patří také do skupiny LC oscilátorů. Princip jejich činnosti je založen na využití aktivního prvku zapojeného paralelně se záporným diferenciálním odporem. Uvažujme paralelní kmitavý obvod. Vybudíme-li tento
obvod libovolným způsobem (např. napěťovým skokem při zapnutí napájecích napětí),
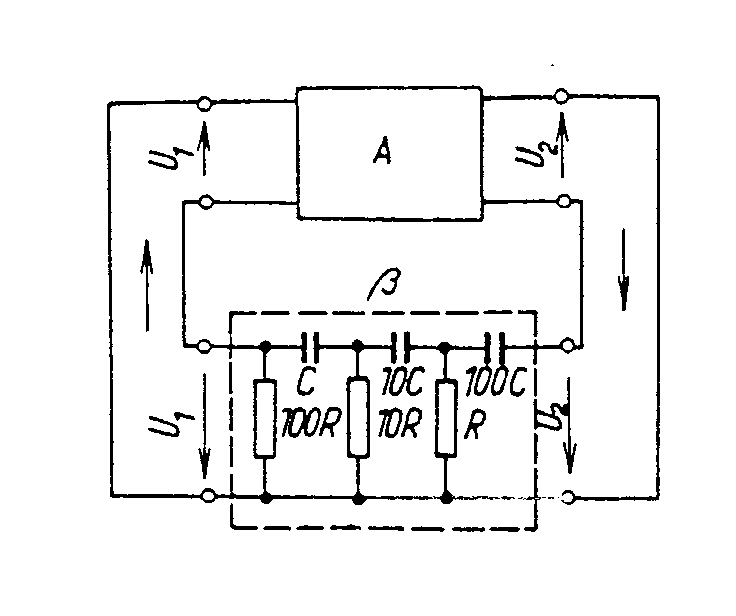
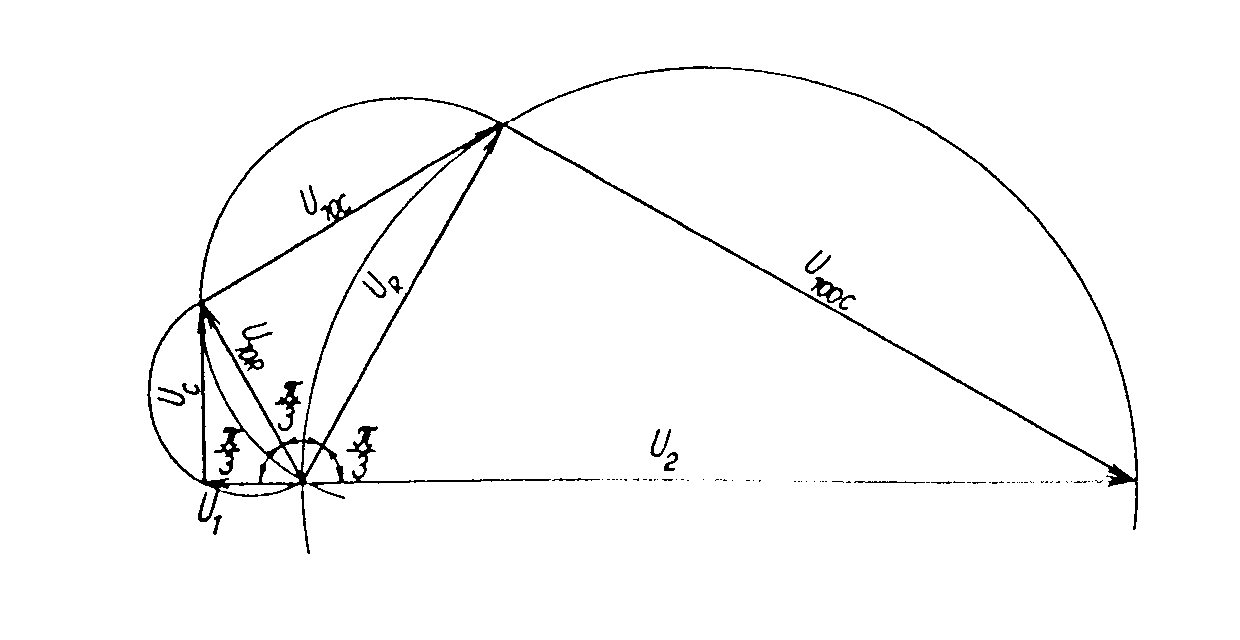
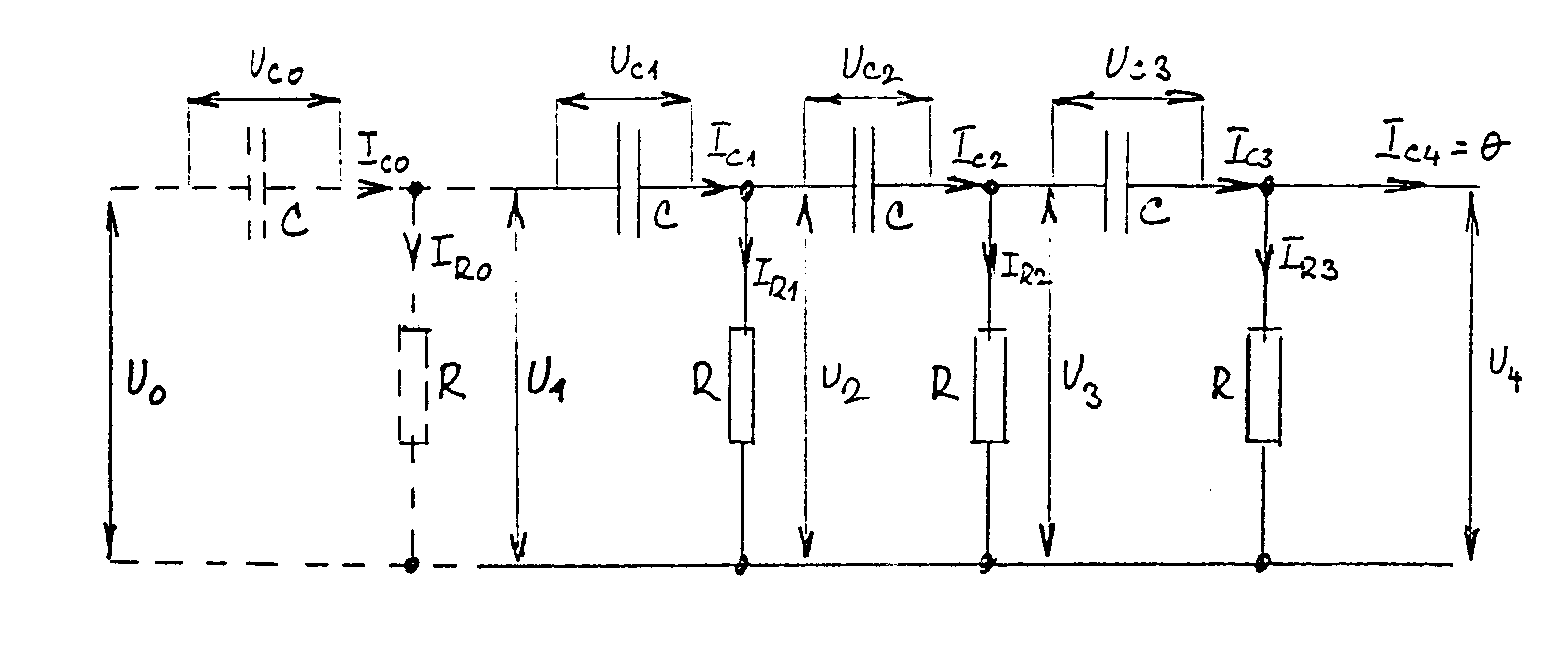
průběh napětí na obvodu bude mít tvar Vidíme, že průběh napětí na kmitavém obvodu může být v závislosti na časové konstantě t trojí: a) je-li t > 0 a konečné, jsou kmity tlumené a v závislosti na čase zanikají s časovou konstantou t b) je-li t < 0 a konečné, narůstají kmity exponenciálně v závislosti na čase c) je-li Q = ¥, je exponent v rovnici roven 0 a obvod kmitá s ustálenou amplitudou. V rezonančním obvodu samotném mohou vzniknout pouze tlumené kmity, poněvadž jeho činitel jakosti je vždy konečný a kladný. Je to způsobeno kladným dynamickým odporem obvodu Připojíme-li ovšem k rezonančnímu obvodu aktivní čtyřpól, který má záporný dynamický odpor -RA = du/di, bude celkový rezonanční odpor dán vztahem Požadujeme-li pro ustálené kmity, aby Q = ¥, musí být R0 = ¥, protože veličiny L a C jsou kladné a konečné. Má-li být R0 = ¥, musí být jmenovatel zlomku roven nule, t.zn, Zůstává otázka, jak získat součástku, jejíž dynamický odpor bude záporný. Existují součástky, jejichž voltampérová charakteristika má tvar znázorněný na obrázku, který nazýváme typem "N". Mezi tyto součástky patří tunelová (Esakiho) dioda, tetroda se sekundární emisí, reflexní klystron a pod. U těchto součástek přechází kladný dynamický odpor na záporný přes nekonečno. Oblast dynamického odporu se vyskytuje pouze v určité části voltampérové charakteristiky. Tyto součástky se rovněž nazývají řízené napětím a v oblasti záporného odporu mohou vytvářet oscilátory ve spolupráci s paralelním kmitavým obvodem. charakteristika typu "N" charakteristika typu "S" Známe ještě charakteristiky typu "S", o nichž přechází kladný odpor na záporný přes nulu. Tyto charakteristiky se nazývají seriové nebo řízené proudem a také obloukové, protože tento jev byl poprvé pozorován u elektrických oblouků. Patří sem plynové výbojky, některé typy vícevrstvých a lavinových diod a pod. Tyto součástky mohou vytvářet oscilátory ve spojení se seriovým kmitavým obvodem. oscilátor typu "N" oscilátor typu "S" Voltampérové charakteristiky tunelové diody se zatěžovací přímkou jsou znázorněné na obr. rostoucí amplituda ustálená amplituda klesající amplituda Zapojení jednobranného ocsilátoru s tunelovou diodou je uvedeno na obr. Potenciometrem se nastaví klidový pracovní bod diody do středu úseku se záporným dynamickým odporem. Harmonické netlumené kmity se ustálí, je-li připojena dioda na takové odbočce cívky, na níž se rezonanční odpor obvodu LC transformuje z hodnoty R¢0/p12 na hodnotu RA. Musí tedy platit pro převod Kdybychom nastavili větší převod, (t.j. posunutí odbočky směrem dolů), mohly by vzniknout v obvodu pouze tlumené kmity. V opačném případě vzniknou kmity s větší amplitudou a větším tvarovým zkreslením napětí v obvodu. RC oscilátory. Pro frekvence nižší, než 100 kHz jsou výhodnější oscilátory RC, protože rezonanční obvody LC pro nižší frekvence jsou již robusní a kvalita rezonančních obvodů klesá. Oscilátory RC patří rovněž do skupiny zpětnovazebních oscilátorů, u nichž je řídící člen proveden pomocí vhodného dvoubranu RC. Otáčí-li řídící člen na rezonanční frekvenci fázi o 180°, musí zesilovací větev, aby byla splněna fázová podmínka otáčet fázi rovněž o 180° nebo o celistvý násobek 2p tohoto úhlu, t.zn jA = (2k+1)p. To znamená, že zesilovč musí mít lichý počet stupňů. Otáčí-li řídící člen fázi o 360° (nebo 0°), musí zesilovač otáčet fázi napětí rovněž o 360 nebo 0°, t.zn. jA = 2kp. Zesilovač musí mít sudý počet stupnů. RC oscilátory s kaskádními čtyřpóly RC. Nejjednodušší RC oscilátory mají řídící člen tvořený kaskádou vazebních členů RC. Aktivní čtyřpól tvoří obyčejně jeden zesilovací stupeň, který otáčí fázi napětí o p, čili jA = p. Podle fázové podmínky je třeba, aby řídící člen měl pro rezonanční kmitočet fázový posun jb = 2kp - jA = 2kp - p = (2k-1)p. k = ±0,1,2,... Nejpoužívanější kaskádní čtyřpól se skládá z 3 vazebních RC článků, z nichž každý může otočit fázi až o 90°. Volme články se stejnou časovou konstantou t = 100RC a rozložme hodnoty rezistorů tak, aby jednotlivé články pracovaly nezatížené. Schema oscilátoru tohoto typu je na obr. Přenosy jednotlivých článků lze uvažovat samostatně. Každý vazební člen s časovou konstantou ti způsobí fázový posun přenášeného signálu s úhlovým kmitočtem w podle vztahu Celkový fázový posun zpětnovazebního čtyřpólu , složeného ze 3 článků bude pro t1 = t2 = t3 = t = 100RC. Pro k=1 plyne z fázové podmínky požadavek jb = p. To je splněno na frekvenci w0, pro kterou platí Tudíž kmitočet oscilací souvisí s obvodovými konstantami podle vztahu Uvedenou situaci lze znázornit na vektorovém diagramu, uvedeném na obr. Z vektorového diagramu lze rovněž odvodit
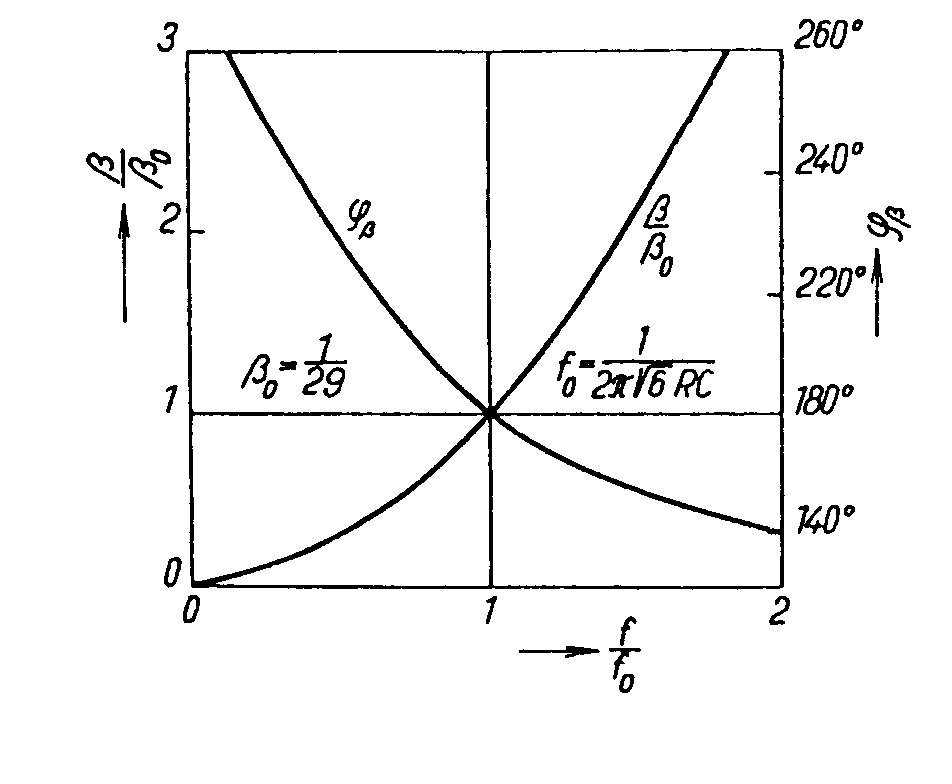
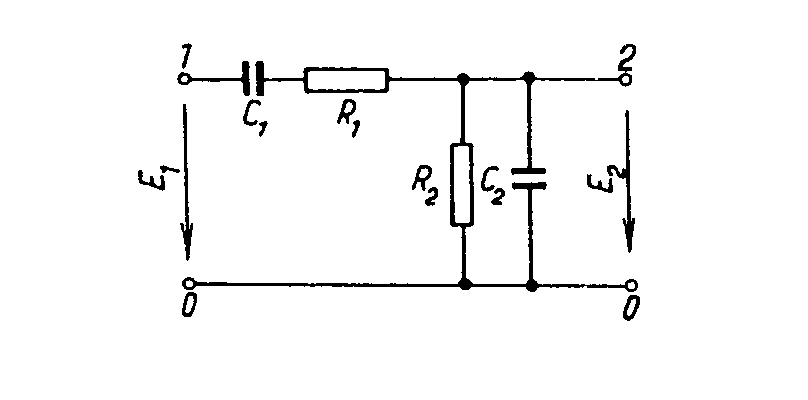
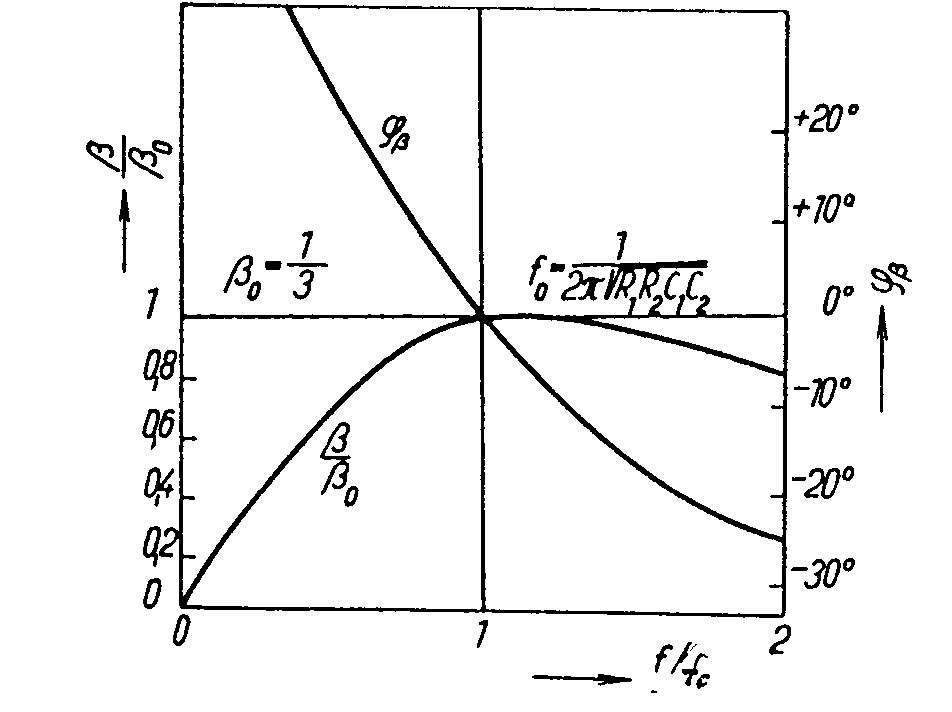
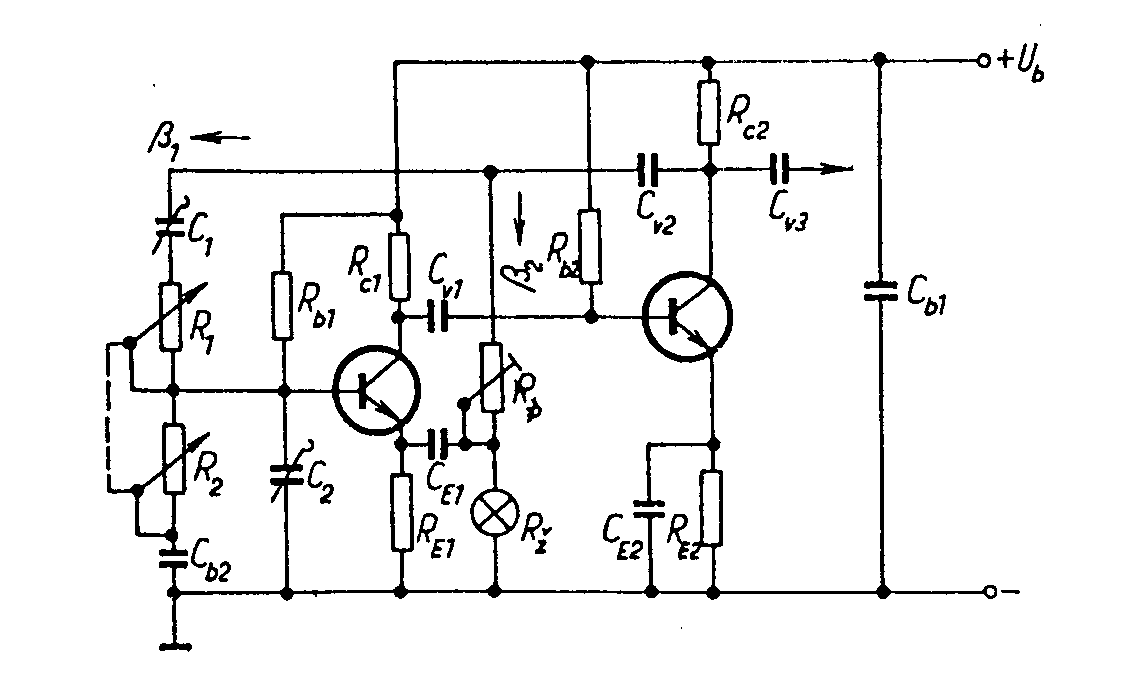
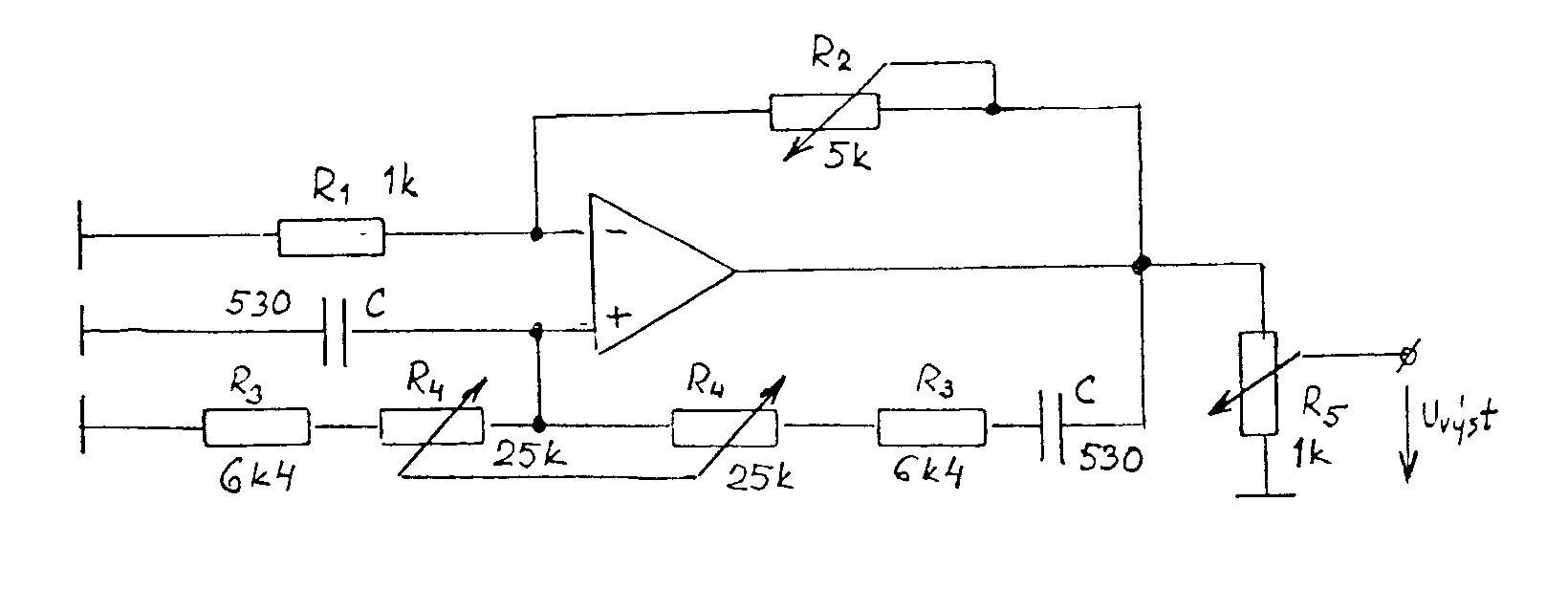
přenos řídícího členu. Platí Odtud přenos zpětnovazebního řídícího členu na oscilačním kmitočtu je Tudíž aktivní čtyřpól musí mít přenos Příklad. Navrhnout RC oscilátor s kaskádními články pro frekvenci f0 = 1kHz R=1kW, předpokládáme-li použití tranzistoru s h11e=1 kHz, h21e = 100. Schema zapojení je Ze vztahu pro rezonanční frekvenci vypočítáme kapacitu Ze vztahu pro zesílení tranzistoru Použijeme kolektorový odpor RC = 100W a potřebné zesílení se nastaví jezdcem potenciometru. Nevýhodou těchto oscilátorů je, že použijeme-li dekadicky odstupňované kapacity a odpory, není vhodný tento oscilátor při požadavku na přelaďování frekvence, protože bychom museli současně měnit 3 různé odpory nebo kondenzátory, což je technicky velmi obtížně realizovatelné. Použijeme-li čtyřpól se stejnými odpory a kapacitami, platí pro zpětnovazební čtyřpól následující vztahy: Obecné řešení: Přenos třístupňového článku je tedy: Pro rezonanční frekvenci platí, že imaginární část přenosu je rovna nule, to znamená: Dosazením do výrazu pro přenos: Uvedené vztahy lze rozšířit na čtyřstupňový článek ( ve schématu naznačeno čárkovaně): Výraz v závorce představuje hledaný přenos. Pro rezonanci opět musí platit, že imaginární část výrazu se musí rovnat nule, t. zn.: Přenos při oscilační frekvenci je tedy: Vidíme, že při třístupňovém zpětnovazebním čtyřpólu se stejnými odpory a kondenzátory vzrostou nároky na zesílení aktivního členu na A = 29. Při čtyřstupňovém čtyřpólu je třeba zesílení A = 18,38. Přesto se tyto typy čtyřpólů používají pro oscilátory, pracující pouze na jedné, nepřelaďované frekvenci. Vlastnosti těchto oscilátorů lze snadno posoudit podle průběhu fázové a útlumové charakteristiky zpětnovazebního čtyřpólu, které jsou pro tříčlánkový čtyřpól uvedeny na obr. Charakteristiky jsou kresleny v závislosti na poměrné frekvenci f/f0. Fázová charakteristika má v okolí rezonanční frekvence malou strmost, což ukazuje na malou stabilitu oscilací. Dále útlumová charakteristika b/b0 nemá v bodě f/f0 vrchol, jako rezonanční křivka LC obvodů, ale při zvětšováním kmitočtu se zvětšuje a amplitudová podmínka je splněna pro všechny kmitočty nad požadovaným kmitočtem f0. To znamená, že v náročnějších případech je nutno zajistit stabilizaci amplitudy kmitů např. pomocí nelineárního prvku, zavádějící zápornou zpětnou vazbu v zesilovači. (V praxi se často používá žárovka v emitorovém obvodu zesilovacího stupně. RC oscilátory s Wienovým článkem. Pro oscilátory, kde požadujeme přeladitelnost je výhodnější zpětnovazební čtyřpól ve tvaru Wienova článku. Wienův článek je znázorněn na obr. Přenos Wienova článku je přenosem impedančního děliče s impedancemi Z1 a Z2, kde impedance Z1 je tvořena seriovou kombinací R1 a C1 a impedance Z2 je dána paralelní kombinací R2 a C2. Odvodíme-li přenos pomocí známé metodiky, dostaneme vztah Existuje tedy jeden kmitočet w0, pro který bude imaginární část výrazu rovna nule, t.zn. a přenos čtyřpólu je čistě reálný a dosahuje maximální hodnotu V praxi se používá zapojení, v němž je R1 = R2 = R, C1 = C2 = C. Potom Průběh útlumové a fázové charakteristiky je znázorněn na obr. Vidíme, že zpětnovazební čtyřpól má na kvazirezonanční frekvenci f0 fázový posuv jb = 0, musí tedy zesilovač rovněž otáčet fázi o 2kp, t.zn. že musí mít sudý počet stupňů. Pro zvětšení stability oscilátorů se zavádí ještě smyčka záporné zpětné vazby. Zapojení oscilátoru s Wienovým článkem je uvedené na obr. Záporná zpětná vazba je realizována obvodem Rp v serii se žárovkou Rž. Oscilační podmínka je tudíž Zmenší-li se např. zesílení zesilovače A, sníží se výstupní napětí oscilátoru. Tím rovněž klesne proud v obvodu žárovky, zmenší se odpor žárovky Rž, klesne vliv záporné zpětné vazby a vzroste vliv kladné zpětné vazby, takže pokles výstupního napětí se téměř vyrovná. Velmi často se jako zesilovač používá operační zesilovač, kde na invertujícím vstupu se nastavuje zesílení zesilovače a na neinvertující vstup je zapojen výstup z Wienova článku. Výhodou oscilátorů s Wienovým článkem je, že pro změnu frekvence stačí měnit jen 2 prvky. Tyto oscilátory se používají v laboratorních podmínkách, kde pomocí 2 tandemových potenciometrů měníme frekvenci v rozsahu 1 dekády a jednotlivé dekády se mění přepínáním kapacit. Příklad. Navrhnout RC oscilátor s Wienovým článkem, f0 = 10-50 kHz, Uvýst =5V. Řešení. Pro střed frekvenčního pásma, t.j f0 = 30kHz vychází Zvolme C = 500 pF. Potom pro dolní konec pásma f0 = 10 kHz je a pro horní konec frekvenčního pásma f0 = 50 kHz je Zvolíme tedy potenciometr R4 = 25 kW v serii s rezistorem R3 = 6k4 Pro R4 = 0, je frekvence pro R4 = 25kW
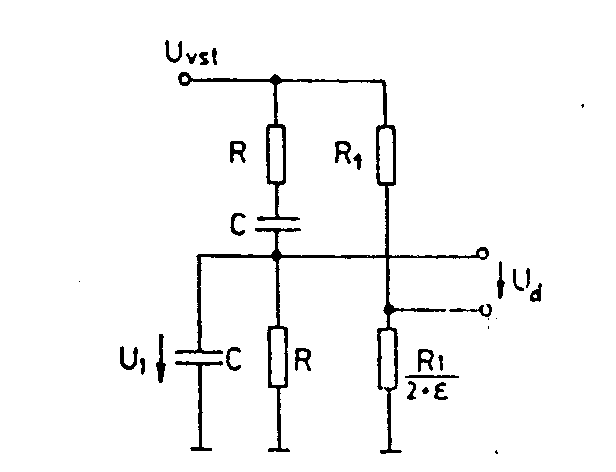
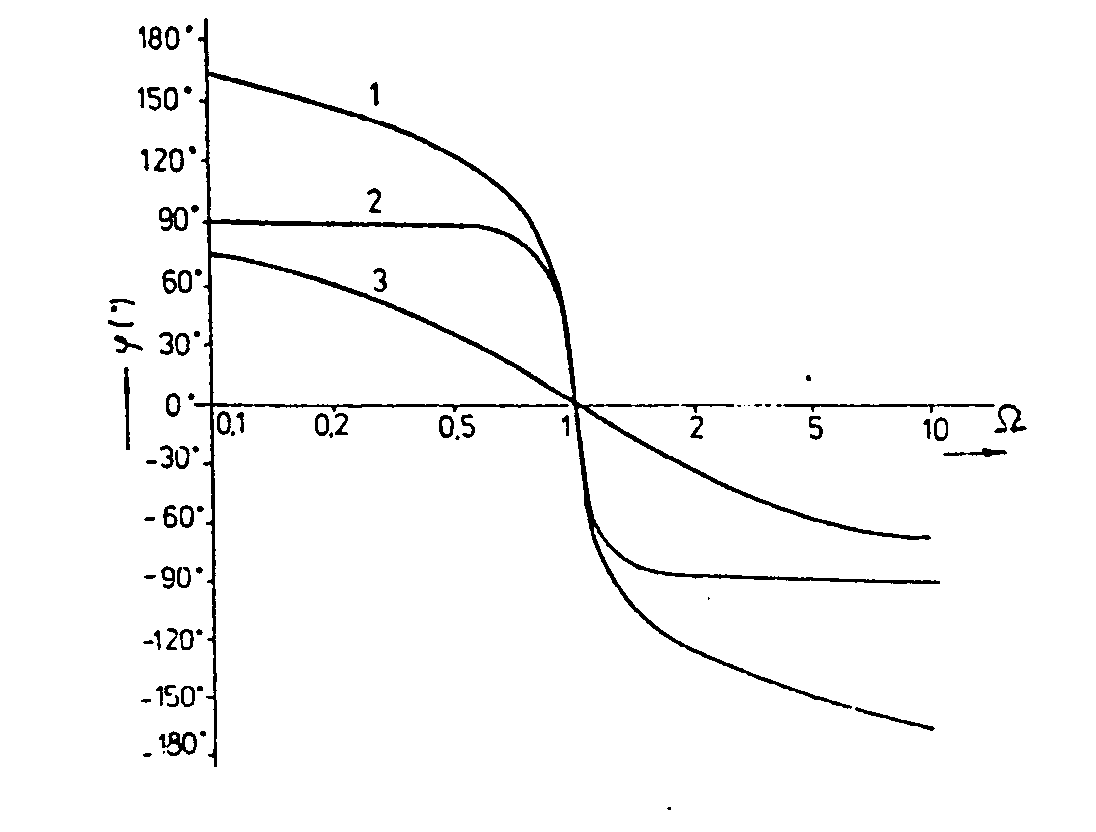
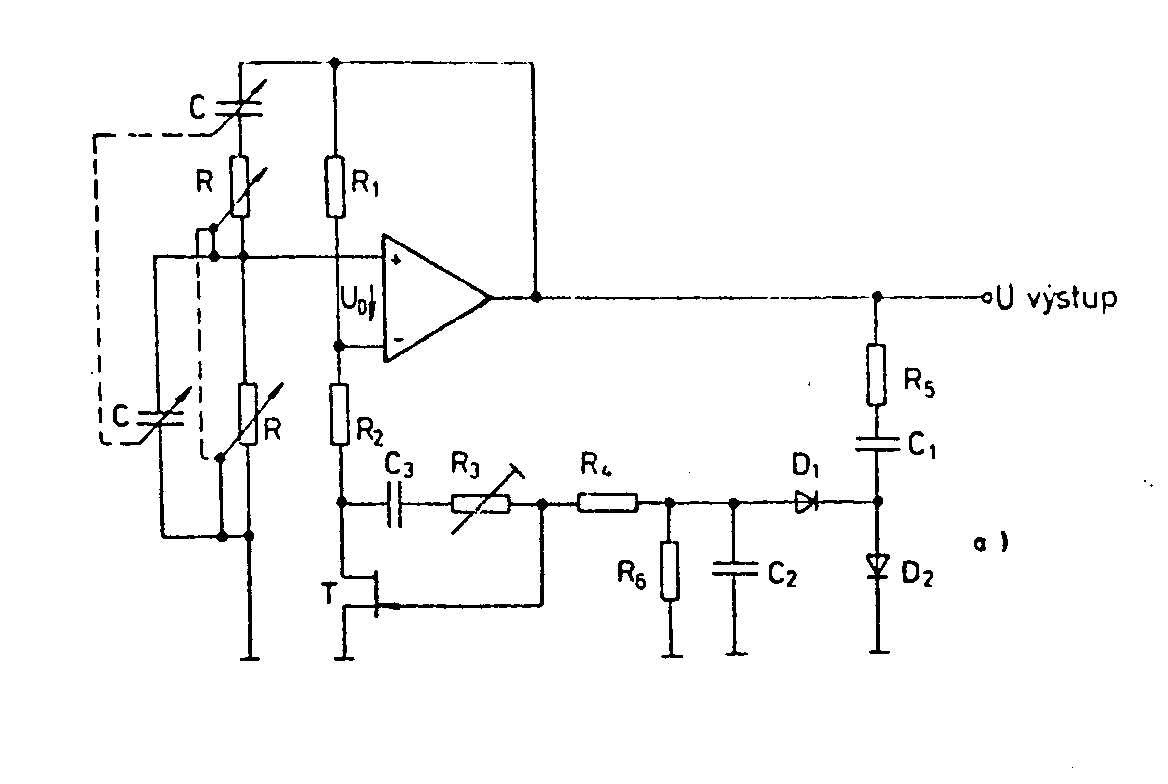
je RC oscilátor s Wienův - Robinovým článkem. Tento oscilátor je odvozen od Wienova oscilátoru. Principielní schema Wienova-Robinova článku je uvedené na obr. Jednu větev můstku tvoří Wienův článek, druhá je tvořena odporovým děličem. Pro e = 0 je v diagonále můstku nulové napětí, t.zn. Ud = 0. Proto musí být e ¹ 0. Potom Pro určení průběhu fáze j je nutno nejdříve vypočítat poměr Ud/Uvst z rovnice Při zanedbání vyšších mocnin W dostaneme Průběh fáze v závislosti na W je uveden na obr. Křivka 1 platí pro Wienův - Robinův můstek, křivka 2 pro paralelní rezonanční obvod s Q=10, křivka 3 pro porovnání pro Wienův článek. Předností Wienův - Robinova můstku je velká strmost fázové charakteristiky v okolí rezonanční frekvence, srovnatelná s kmitavým obvodem s vysokým činitelem kvality. Nevýhodou je velký útlum při rezonanční frekvenci, tím větší, čím menší se volí e. Obecně je poměr Ud/Uvst = k = e/9. Pro splnění amplitudové podmínky kA = 1 musí mít zesilovač rozdílové zesílení rovno A=1/k=9/e. Pro e = 0,01 je třeba A=900. Je-li A větší, roste rychle amplituda kmitů a zesilovač je přebuzen. Při menším A kmity rychle zaniknou. Rezistory R1 a R1/2+e nelze vybrat s dostatečnou přesností. Proto se místo rezistoru R1/2+e používá unipolární JFET tranzistor, jehož kanálový odpor mezi kolektorem a emitorem lze řídit pomocí napětí na jeho hradle. Kanálový odpor RCE závisí na napětí UCE, je-li napětí UCE malé. Proto se vytvoří takový úbytek napětí na odporu R2, aby mělo seriové spojení R2 a RCE hodnotu R1/2+e. Nejmenší hodnota RCE je RCEmin. Odpor R2 musí být menší než R1/2 - RCEmin. Po připojení provozního napětí je nejprve Uvst nulové a tedy RCE = RCEmin. Je-li splněna uvedená podmínka, je výsledný odpor R2 a RCEmin menší než R1/2. Při rezonanční frekvenci je tedy rozdílové napětí relativně vysoké. Výstupní napětí zesilovače se usměrní napěťovým zdvojovačem D1D2 (viz obr.), potenciál hradla se stane zápornější a RCE se zvětší. Výstupní amplituda roste tak dlouho, až platí rovnost Činitel zkreslení závisí na linearitě výstupní charakteristiky unipolárního tranzistoru, Tu lze zlepšit zavedením záporné zpětné vazby z výstupu tranzistoru na jeho hradlo pomocí odporů R3 a R4. Kondenzátor C3 zabraňuje průniku stejnosměrného proudu na hradlo, který by mohl posunout pracovní bod na výstupu. Jemným nastavením R3 lze dosáhnout minimální zkreslení až 0,1%. V praxi se volí R3 = R4.
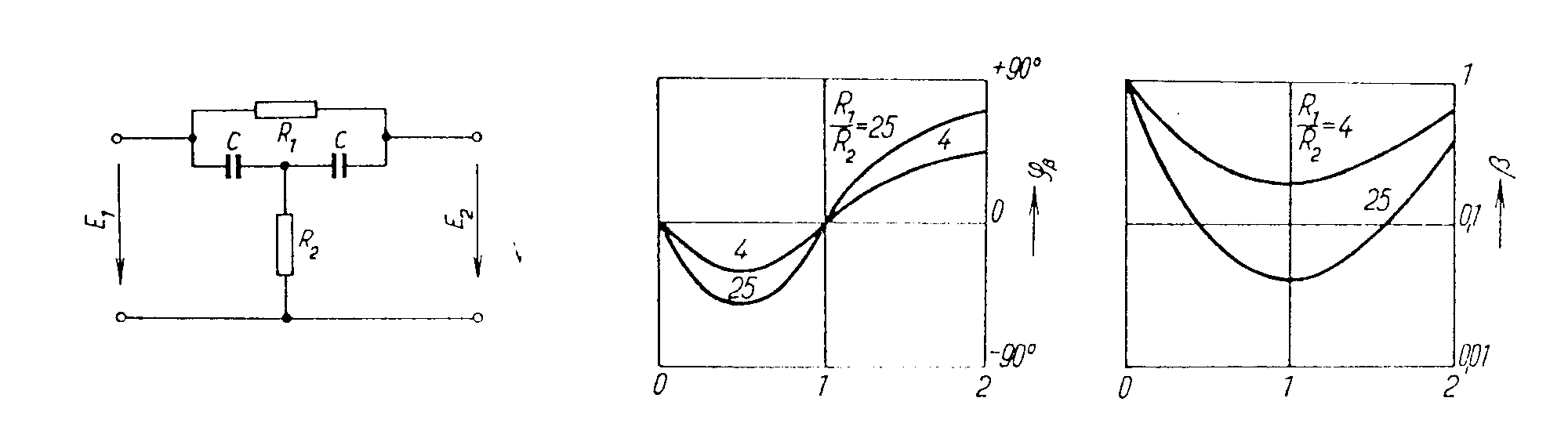
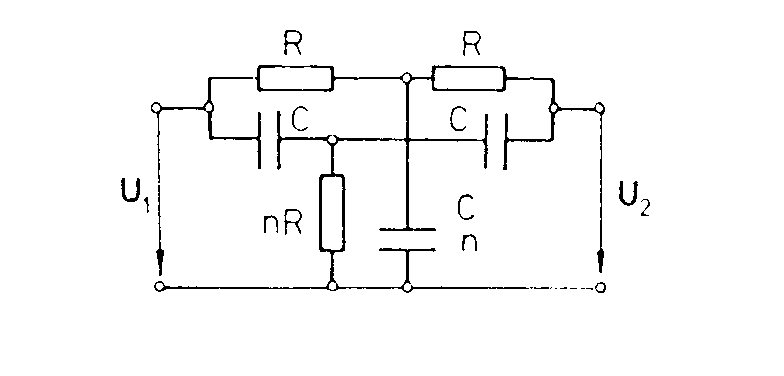
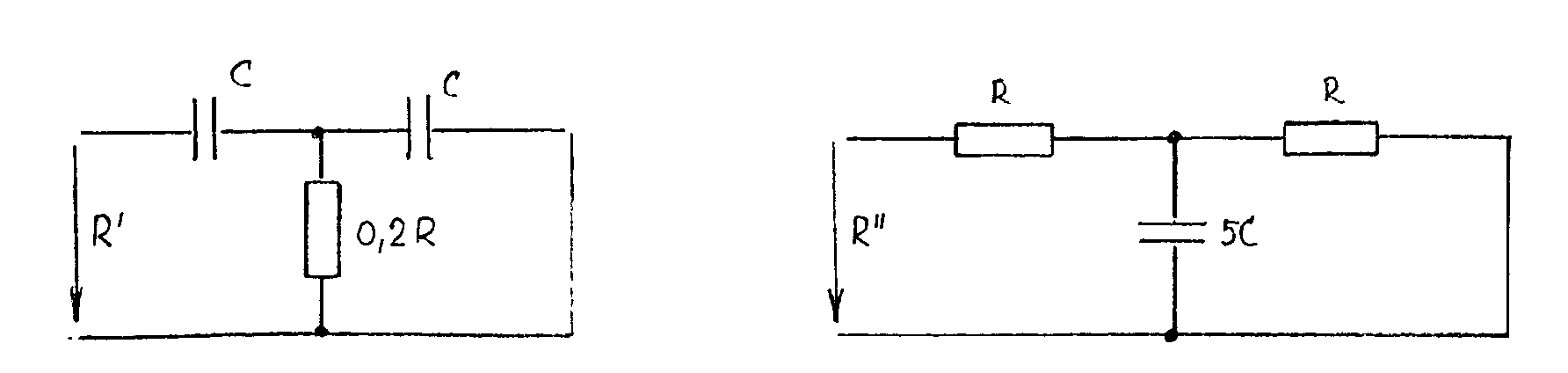
RC oscilátor s přemostěným T článkem. Jako zpětnovazební čtyřpól lze použít rovněž přemostěný T článek. Jeho zapojení a charakteristiky jsou uvedené na obr. Kvazirezonanční kmitočet je dán vztahem a na něm dosahuje přenos minimální velikost Principielní schéma oscilátoru je uvedené na obr. První tranzistor je zapojen se společnýn emitorem, druhý tranzistor pracuje jako emitorový sledovač. Mezi emitory je zapojena žárovka, která zavádí kladnou zpětnou vazbu. Není-li připojen T článek, rozkmitá se zesilovač na kmitočtu, daném pouze časovými konstantami v obvodu zesilovače. Připojením T článku se zavede do obvodu silná záporná zpětná vazba, která je nejmenší na kmitočtu f0. Při vhodném poměru kladné zpětné vazby přes nelineární odpor žárovky a záporné zpštné vazby přes T článek se zesilovač rozkmitá na kvazirezonančním kmitočtu f0. Žárovka působí jako stabilizátor vnitřních poměrů v zesilovači a tím i výstupního napětí. RC oscilátor s dvojitým T článkem. Dvojitý T článek je znázorněn na obr.
Protože tyto oscilátory pracují obyčejně ve spojení
s jednostupňovým zesilovačem, navrhujeme parametry T článku tak, aby jeho
přenos byl maximální a záporný. Kvazirezonanční frekvence T-článku je
Derivováním tohoto vztahu zjistíme,
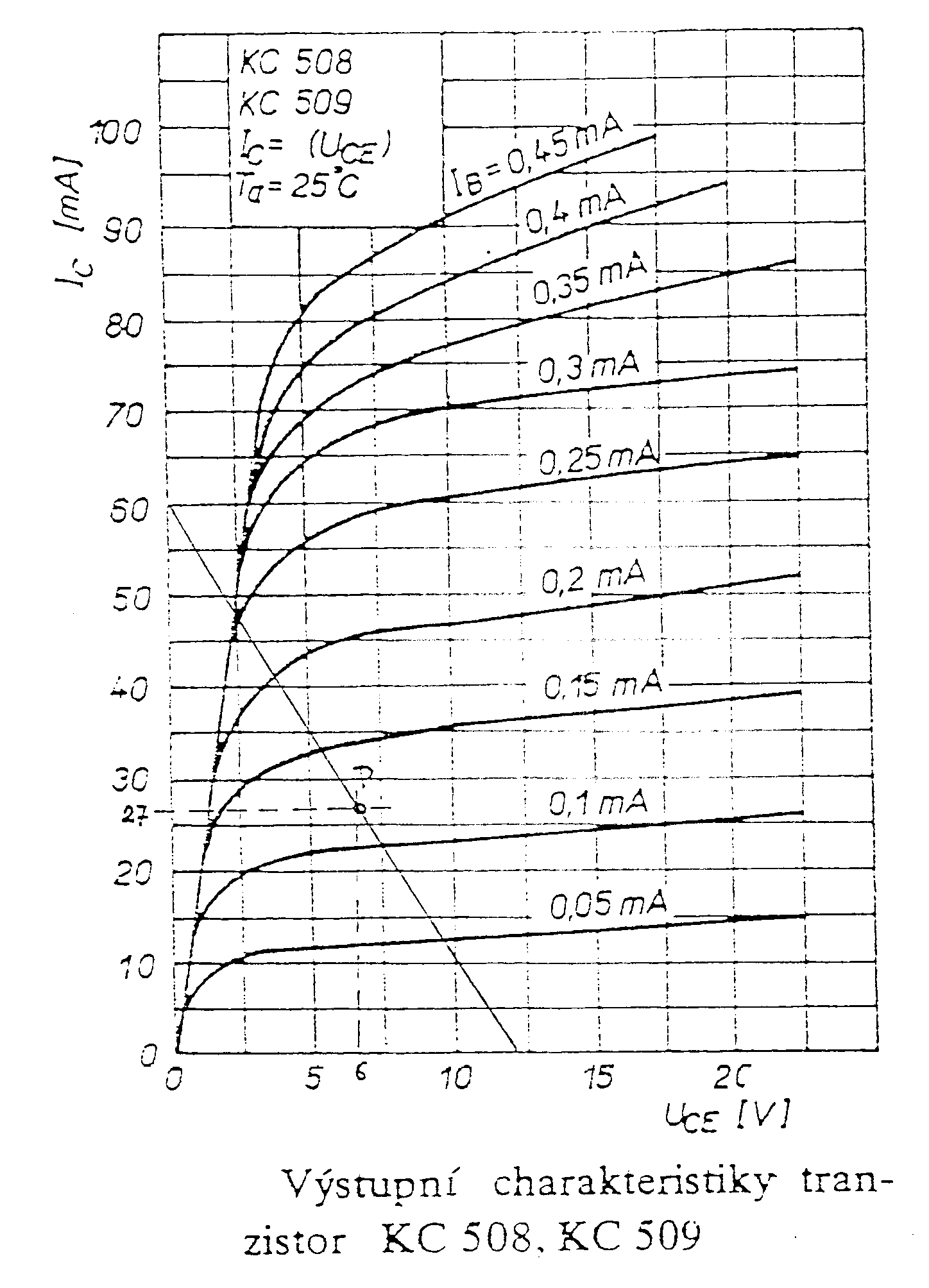
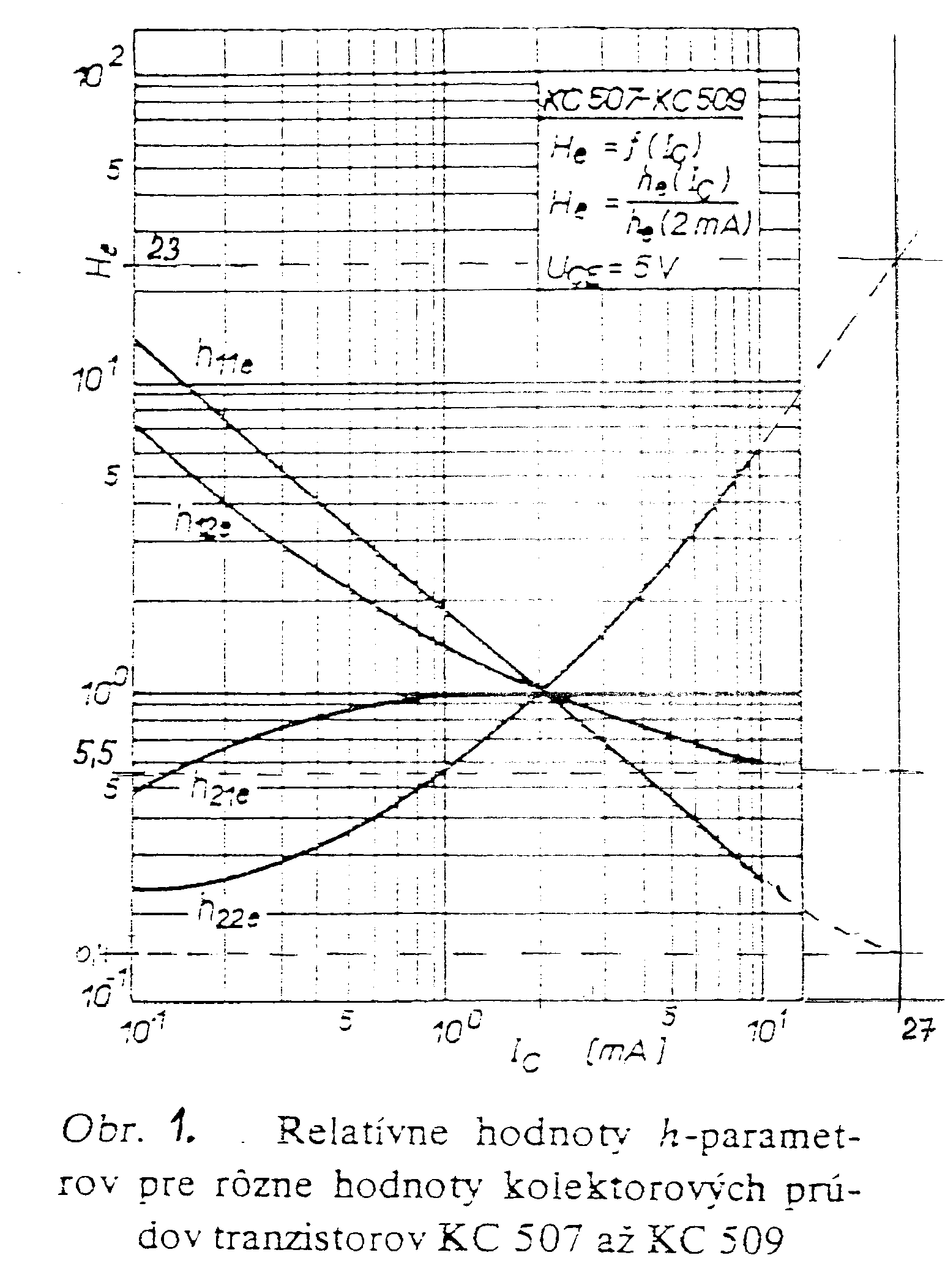
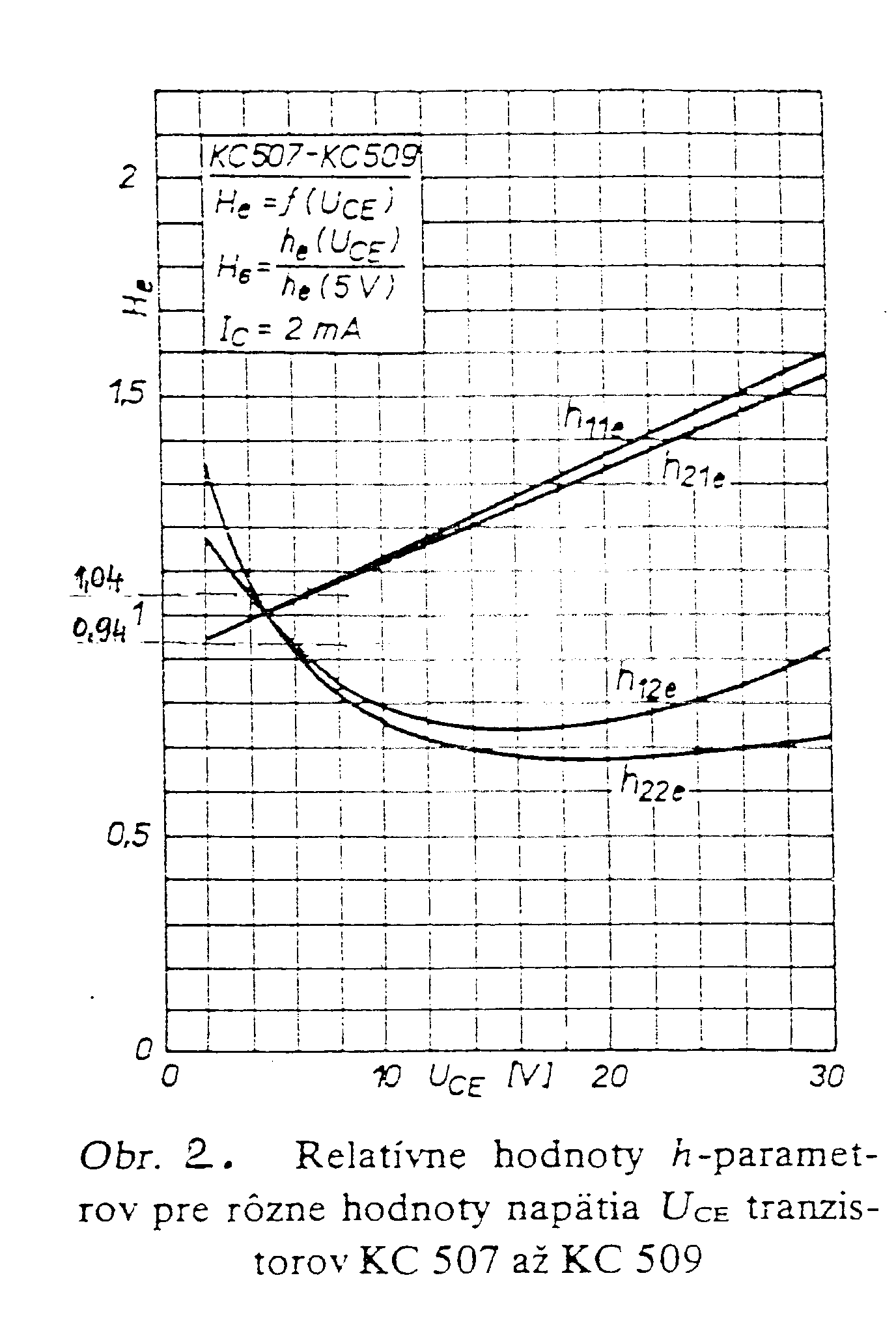
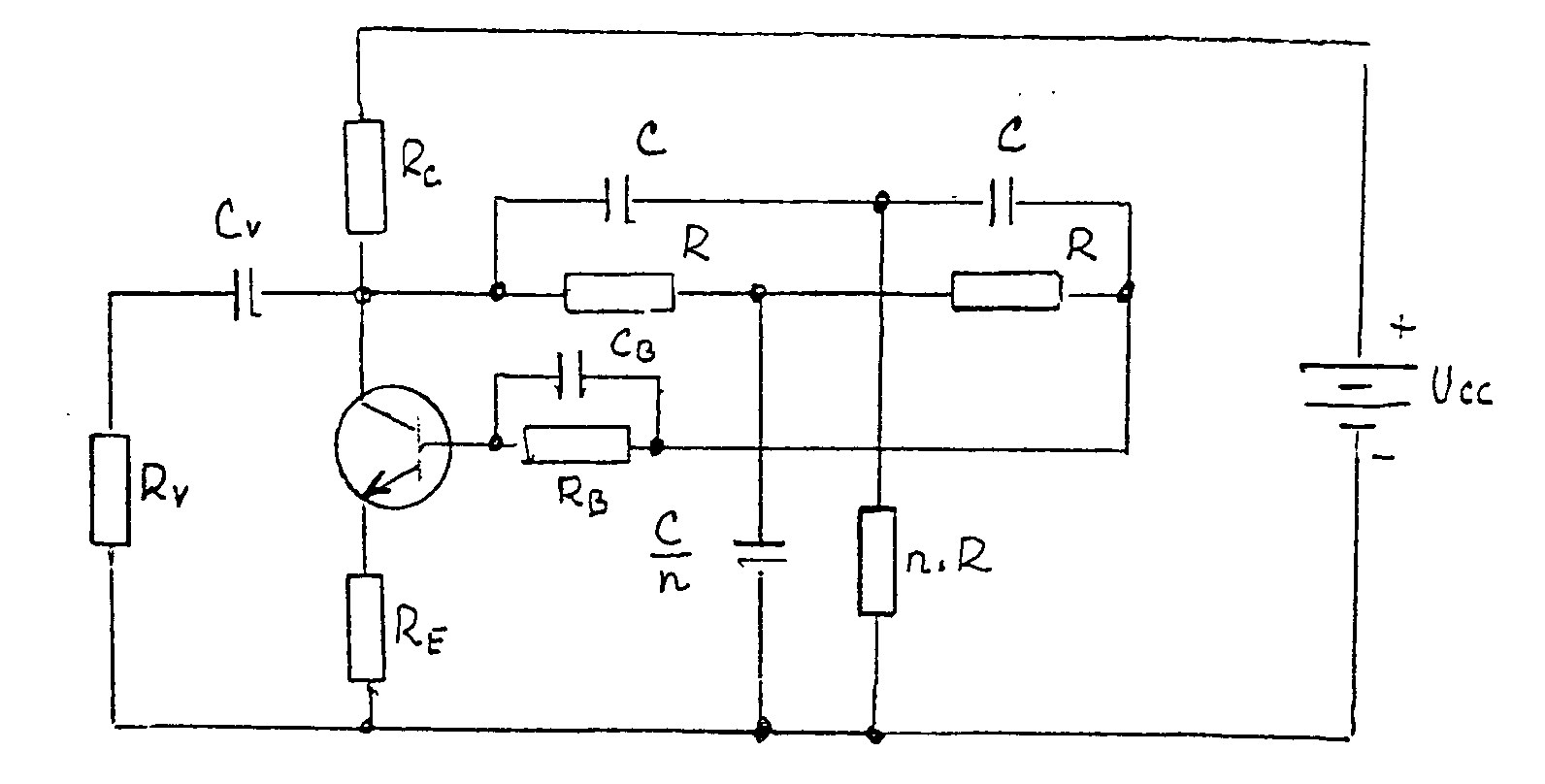
že Volí se tedy obyčejně n = 0,2. Způsob návrhu je uveden v následujícím příkladu. RC oscilátor s dvojitým T - článkem. Zadání: Navrhněte RC oscilátor s dvojitým T - článkem, je-li zadáno: f = 1kHz, UCC = 12V, Rz = 1kW. Použijte tranzistor KC 509, který má v pracovním bodě UCE = 5V a IC = 2 mA parametry: h11e = 8,7kW, h12e = 3.10-4, h21e = 300, h22e = 60 mS. Řešení. V soustavě výstupních charakteristik volíme výsledný pracovní odpor tranzistoru Rprac = 200W. Pracovní bod tranzistoru volíme v bodě UCE0 = 6V, IC0 = 27mA (viz charakteristiky tranzistoru na konci příkladu). Přepočet h-parametrů do zvoleného pracovního bodu: Výpočet dvojitého T-článku: Přenos dvojitého T-článku na rezonanční frekvenci
je: Předpokládáme-li jednostupňový zesilovač, požadujeme aby přenos článku byl záporný a maximální. Derivací uvedeného vztahu podle n dostaneme: A(f0)max = -0,093 při n=0,207. Volíme tedy n=0,2. A(f0)=-0,1. Předpokládané schéma oscilátoru je na obr. Volíme hodnotu Výpočet vstupního odporu T-článku. T-článek představuje dva paralelně řazené obvody,
s vstupními odpory Absolutní hodnota impedance Absolutní hodnota impedance Vstupní odpor T-článku je Pracovní odpor je dán paralelní kombinací kolektorového odporu RC, vstupního odporu T-článku Rvst a zatěžovacího odporu Rz. Je tedy hodnota kolektorového odporu rovna Předpokládejme nejdříve, že emitorový odpor RE = 0. Při klidovém proudu IC0=27mA může být rozkmit střídavého proudu Icmax=17mA, t,j. efektivní hodnota střídavého proudu je IC1 = 12mA (viz charakteristiky KC 509). Na pracovním odporu Rprac, t.j. na kolektoru
tranzistoru bude střídavé napětí Při přenosu T-článku A = 0,1 bude na bázi tranzistoru střídavé napětí Z definice parametru y21E plyne: Odpor v bázi Vstupní odpor zesilovacího stupně předpokládejme roven h11E (přesným výpočtem vyjde 3,56kW). Kondenzátor CB musí mít na pracovní frekvenci impedanci nejméně o řád menší, než je h11E.
Vazební kondenzátor V příloze jsou uvedené grafy pro přepočet h-parametrů tranzistoru a výstupní chararakteristiky, pro volbu pracovního bodu. Literatura : 1) Vačkář, Marvánek, Radioelektronická zařízení pro 4. ročník SPŠ elektrotechnických, SNTL Praha 1982, Dvořáček a kol., 2) Kurs radiotechniky, SNTL Praha 1975, 3) Maťátko, Elektronika |
|
zpět na předchozí stránku
Copyright © 2003 Hell
doporučené rozlišení 1024x768

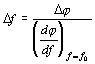 .
.
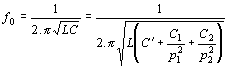 . Tento vztah již obsahuje některé konkrétní veličiny, nazývá se kmitočtová
podmínka a hodí se pro návrh LC oscilátorů.
. Tento vztah již obsahuje některé konkrétní veličiny, nazývá se kmitočtová
podmínka a hodí se pro návrh LC oscilátorů. 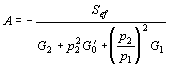 . Napěťový přenos zpětnovazebního čtyřpólu je
. Napěťový přenos zpětnovazebního čtyřpólu je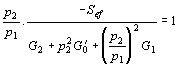 .
. 
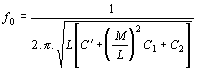
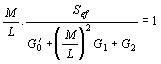
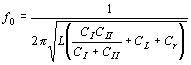
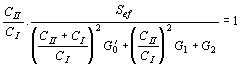
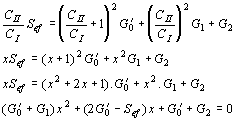
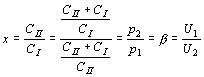
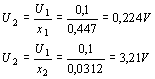
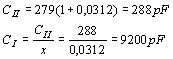
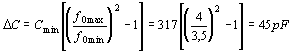
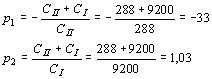
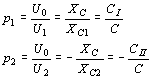
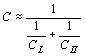
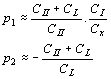
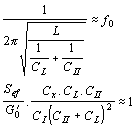
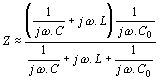 pro R = 0.
pro R = 0.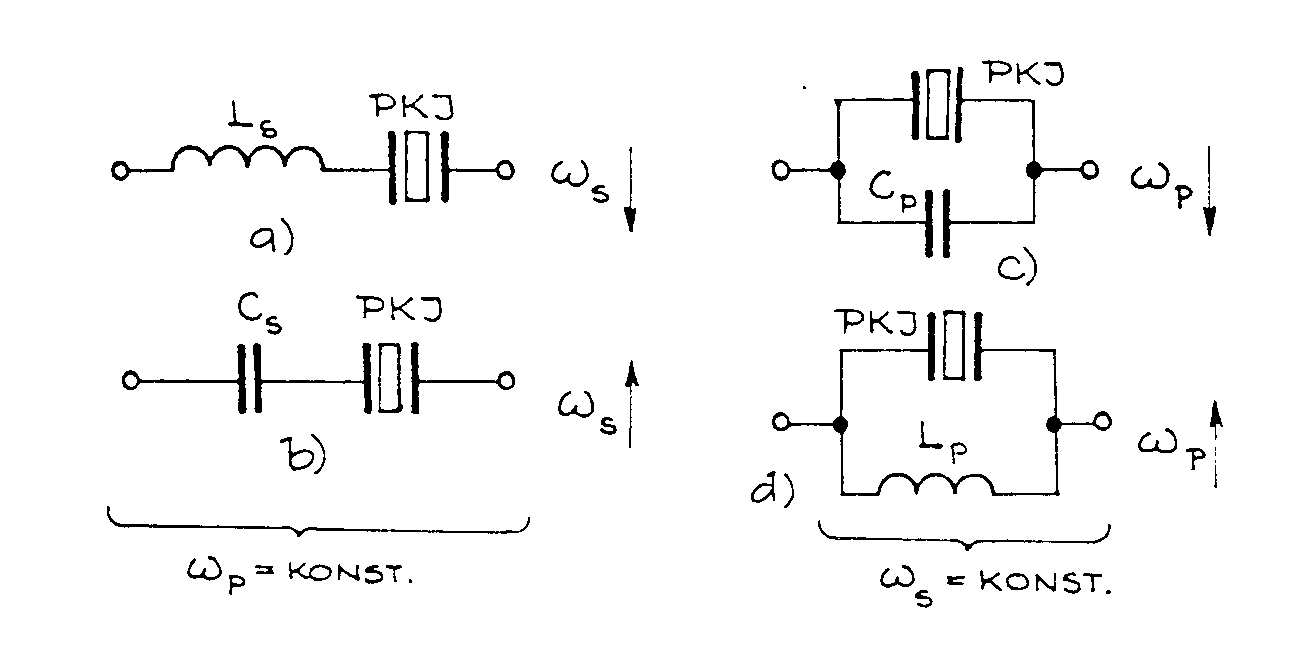
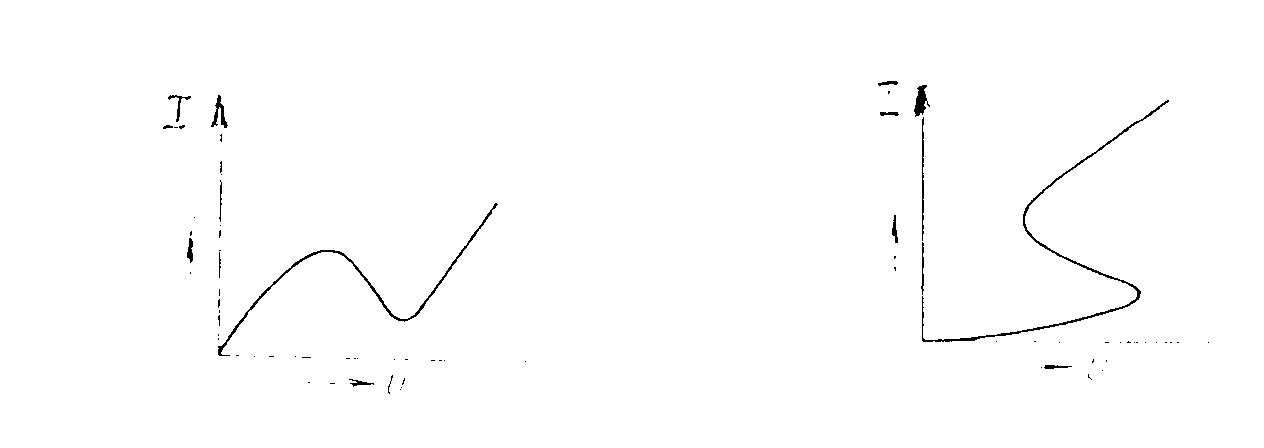

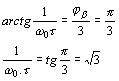
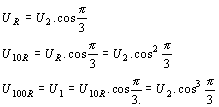
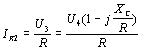
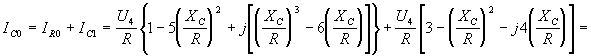
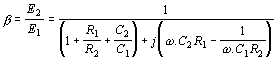
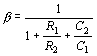
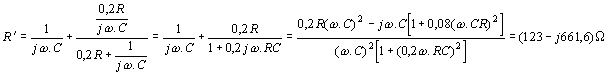
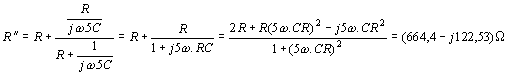
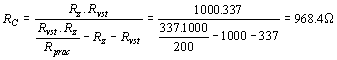 . Volíme RC = 1k
. Volíme RC = 1k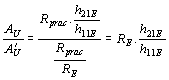 . Z toho dostaneme
. Z toho dostaneme