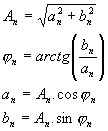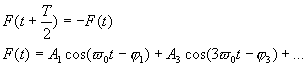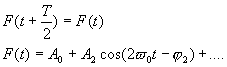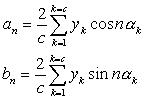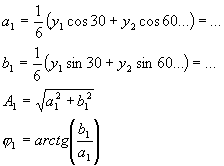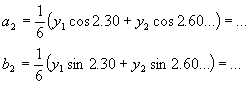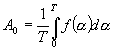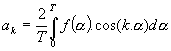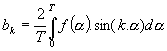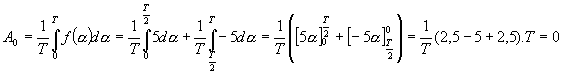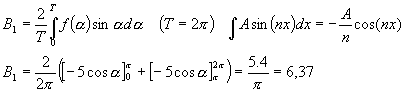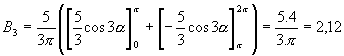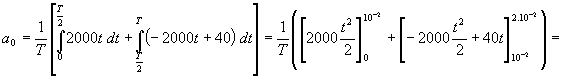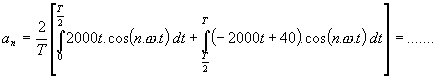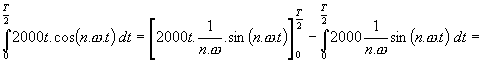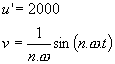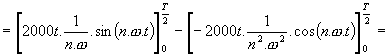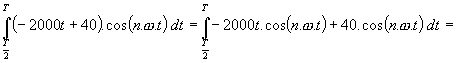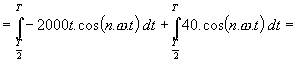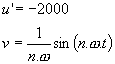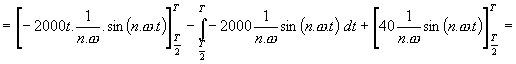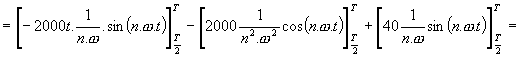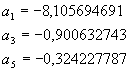Elektronika

Maturitní otázky

HARMONICKÁ ANALÝZA

48.Harmonická analýza

Při řešení obvodů s veličinami složitých časově proměnných obvodů lze zjednodušit tím, že časově proměnnou veličinu nahradíme veličinou, jejíž průběh je popsán jednoduchou funkcí a její působení je z hlediska řešení rovnocenné. Vhodnými jednoduchými průběhy jsou :

a)       signál stejnosměrný stálý

b)       sinusový nebo kosinusový

Pro stejnosměrný stálý signál jsou definovány 2 hodnoty :

a)       střední hodnota : Hodnota stejnosměrného proudu, který přenese za dobu t stejný elektrický náboj

b)       efektivní hodnota : Hodnota stejnosměrného stálého proudu, který za stejnou dobu t vykoná na stejném rezistoru stejnou práci jako uvažovaný proud

Periodické signály nesinusového tvaru lze nahradit velkým množstvím sinusových a kosinusových harmonických průběhů – nazývají se harmonickými složkami a touto teorií rozkladu signálu se zabývá Harmonická analýza.

Základ : Fourierova věta – každá jednoznačně určená periodická funkce s opakující se periodu T a opakovacím kmitočtem f₀ (f₀ = 1/T ), která má v intervalu konečný počet extrémů  a nespojitostí může být vyjádřena nekonečnou geometrickou řadou.

Toto je Fourierův rozvoj. Kde w₀ je základní frekvence, a₀ je střední hodnota, a_1…n jsou kosinusové složky, b_1…n jsou sinusové složky, 1..n-tá harmonická,  a a_1…n , b_1…n jsou Fourierovy součinitele.

– základní harmonická

– vyšší harmonické

Známe-li součinitele pro jeden tvar můžeme vypočítat tvar druhý :

Zjednodušení fourierova rozvoje :

1) průběh je souměrný podle počátku

2) průběh je souměrný podle osy y

3) souměrnost podle osy x

4) opakují se dva stejné impulsy

Provedení harmonické analýzy : úkolem je určení pro danou funkci, hodnoty součinitele a_1…n , b_1…n a nebo amplitudovou A_n a fázový posun j_n jednotlivých harmonických, přičemž n je 1,2,3…

Metody :

Numerická metoda

Grafická metoda

Matematická metoda

            Měření na harmonických analyzátorech

Numerická metoda

Úkolem je provést harmonickou analýzu průběhu, jehož analytické vyjádření neznáme. Průběh je dán graficky.

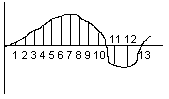
Periodu 2p rozdělíme na c stejných dílků a n je harmonická, kterou chceme zjistit.

n je ta harmonická(nejvyšší), kterou chcem zjistit. Čím víc c tím je přesnější výsledek, ale ztíží se vypočet. Čas t v řadě nahradíme úhlem a = wt a periodu t úhlem 2p.

Stejnosměrná složka :

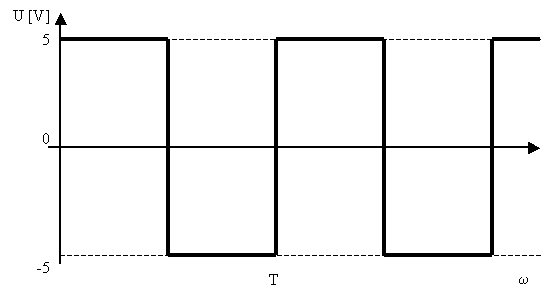
y_k odečteme z našeho signálu, pro každý bod zvlášť. Př: y₁= 13, y₂ = 25, …

Výpočet pro 1.harmonickou :  pro n = 1

Výpočet pro 2.harmonickou :  pro n = 2

Grafická metoda

Každou funkční hodnotu y_k si představíme jako fázor svírající úhel a_k s kladnou poloosou a výsledný fázor je průmětem do osy vodorovné (y_k sin n a_k), svislé (y_k cos n a_k).

Rozdělíme si po tolika stupních kolikátou harmonickou počítáme, čím vyšší tím méně. Pokaždé polovina. Začínáme s tolika částmi úhlu, jako si rozdělíme náš signál.

Matematická metoda

Pro SS složku :

Pro cos složku :

Pro sin složku :

Integrály jsou uvedeny pro úhlovou oblast, pro časovou oblast se položí a=w.t.

Při výpočtu užíváme zjednodušení pomocí liché nebo sudé funkce nebo pouze lichých nebo sudých harmonických. Pro další zjednodušení výpočtu musíme vzít v úvahu, že lze počátek ve většině funkcí libovolně měnit ( ale ne všude ). Dalším zjednodušení umožňuje posuv signálu ve svislém směru – SS složka se určí z neposunutého směru a další činitele se určí z posunutí. Posunem je řada hodnot nulová a potřebné součiny není nutno počítat.

Př.: Výpočet spektra obdélníkového signálu

U = ±5V

f = 1KHz

T = 1ms

Vzhledem k tomu, že kladná i záporná plocha signálu jsou stejně velké, jedná se o klasický signál s nulovou SS složkou.

Signál splňuje podmínku, že stačí spočítat pouze liché harmonické. Počátek zvolíme tak, abychom počítaly pouze sinusové složky signálu.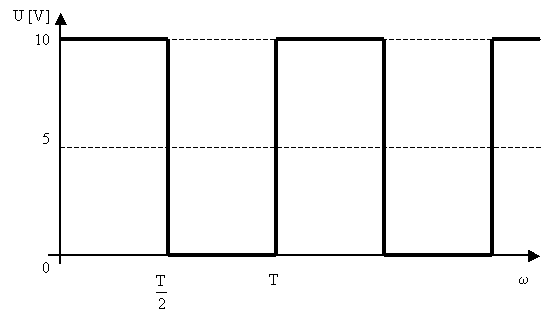

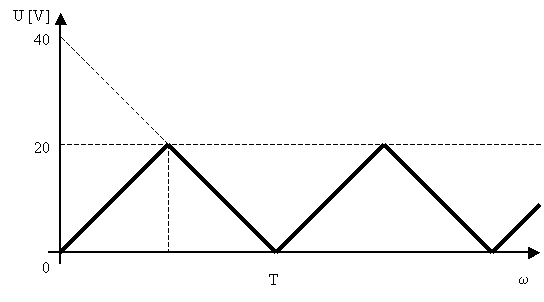
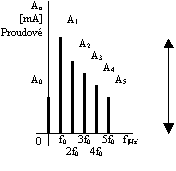
Stejným způsobem se vypočítá třetí a zbývající harmonické složky signálu.

atd.

Nakonec vytvoříme amplitudové spektrum do grafu. Zde bude vyneseno na ose y U[V] a na ose x f[Hz].

Př.: Výpočet spektra trojúhelníkového signálu

T = 20.10^-3s

U = 20 V

Rovnice přímky :

Řešíme ve dvou intervalech :

Interval                    

Interval

Střední hodnota :

Funkce je sudá (souměrná podle osy Y), takže se uplatní pouze cos složky, sin složky jsou rovny 0. Dále funkce je periodická v kladné části osy Y : , proto vypadnou všechny liché členy. Bude obsahovat pouze sudé členy.

Cos složky :

1. vypočítáme první integrál :

Celý první člen se složkou sin vypadne ( je nulový ), protože , kde x je jakékoliv celé sudé číslo, je roven 0.

2. vypočítáme druhý integrál :

Celý první a třetí člen se složkou sin vypadne ( je nulový ), protože , kde x je jakékoliv celé sudé číslo, je roven 0.

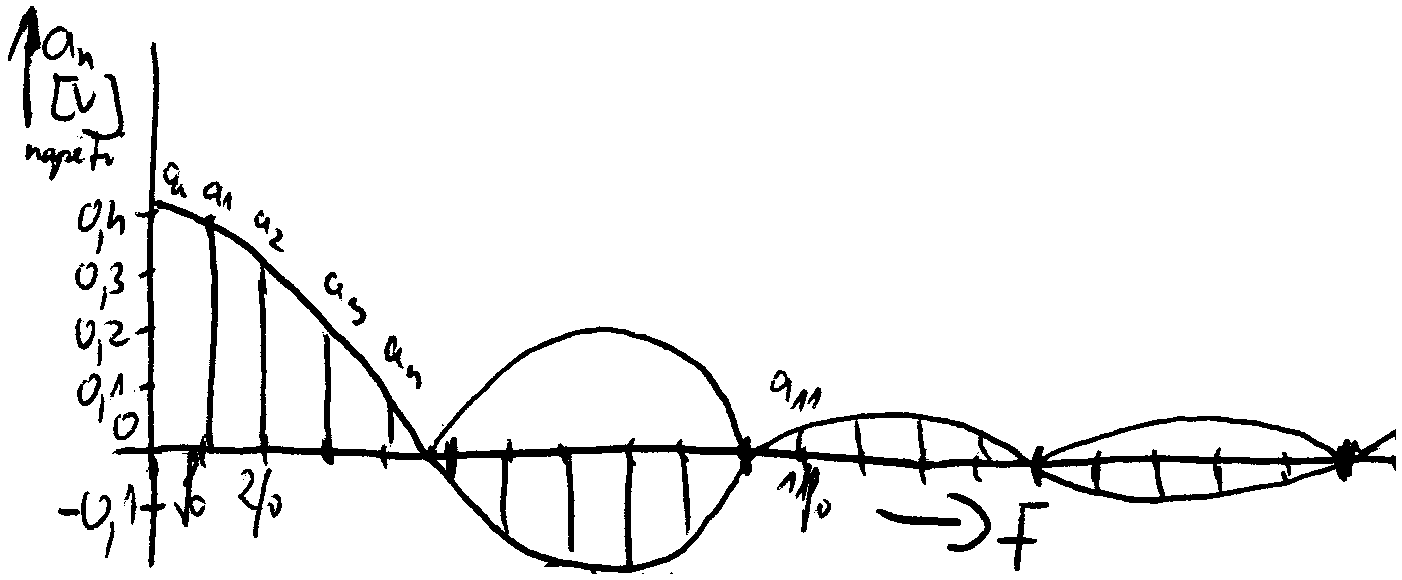
Kmitočtové spektrum

Výsledek Harmonické analýzy je zapsán většinou formou úplné fourierovy řady. Vzhledem k tomu, že velikost amplitudy A₁ až A_n je příspěvek každé harmonické dostatečně určen, je výstižnější popsat funkci pomocí amplitud. Tato posloupnost se nazývá amplitudové spektrum funkce.

			Spektrální čáry, nespojité, čárové (diskrétní)

Amplitudové spektrum se doplňuje spektrem fázovým  j_n.

Místo Amplitudového spektra se můžou vynášet spektra sin a cos složek.