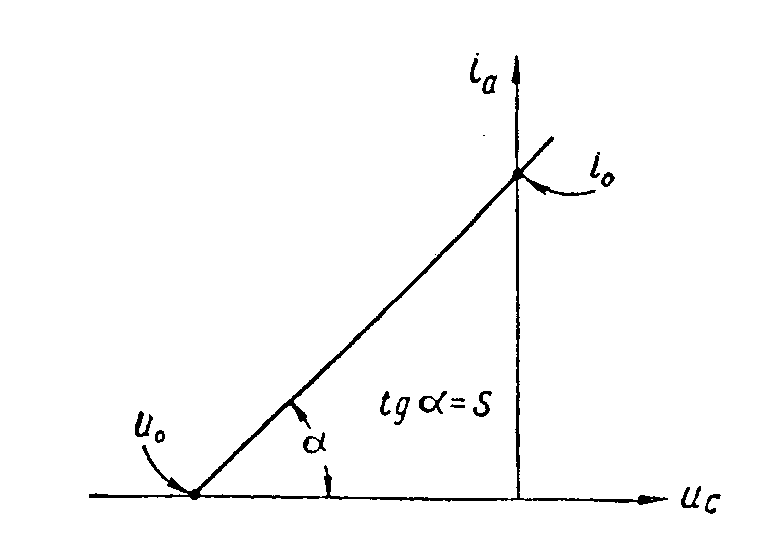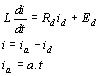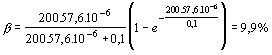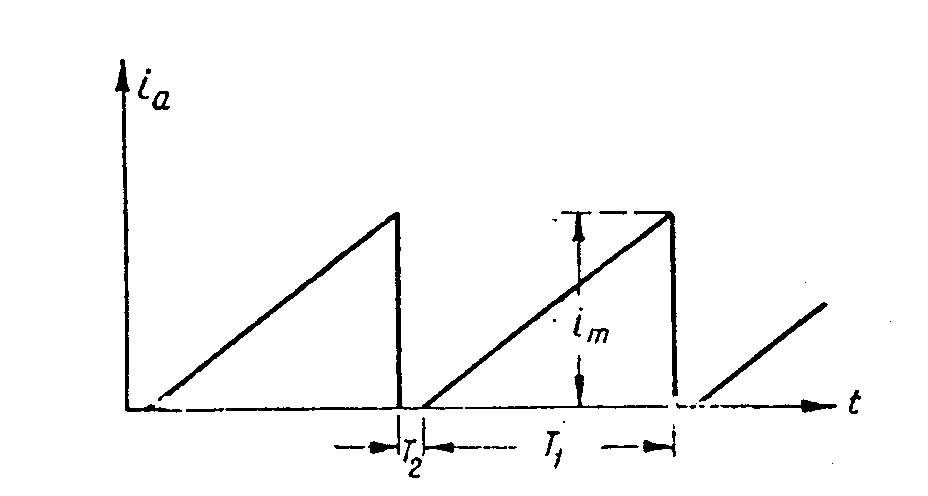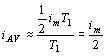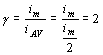|
|
HŘÍŠNÍCI NOVÝ UŽIVATEL nepřihlášený uživatel Právě si tyto stránky čte 1 člověk. |
|
Poslední změna:
29.09.2007 |
|
Návštěvník číslo: 26421 |
| ICQ:61783389 |
|
Copyright © 2003 Hell |
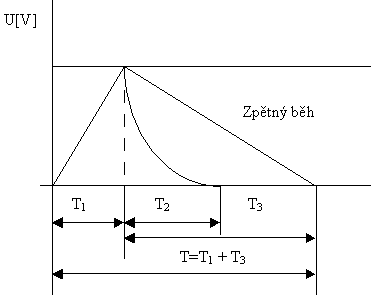
ElektronikaMaturitní otázkyGENERÁTORY PILOVÝCH PRŮBĚHŮ51. Generátory pilových průběhů Napětí pilových nebo trojúhelníkových průběhů se používají v rozkladových generátorech obrazovek, v obvodech pro automatický záznam voltampérových charakteristik, v obvodech fázového řízení a při dalších aplikacích. Pro vychylování paprsku v osciloskopech s elektrostatickým vychylováním elektronového paprsku se používají generátory pilového napětí (nazývají se generátory časové základny), v zařízeních s elektromagnetickým vychylováním elektronového paprsku se používají generátory pilového proudu (nazývané rozkladové generátory). Základní pojmy, princip funkce generátorů pilového napětí. V době přímého běhu T1 se má napětí zvětšovat lineárně s časem až na maximální hodnotu a v době zpětného běhu T2 má klesnout na nulu, nebo na počáteční hodnotu.U pilových průběhů se požadavky na průběh zpětného běhu nekladou, u trojúhelníkových průběhů musí být i zpětný běh T3 lineární funkcí času. Doba periody T = T1 + T2, resp. T = T1 + T3. Opakovací kmitočet je f = 1/T.
Genarátory pilových napětí. Nabíjíme-li kondenzátor přes odpor, platí pro náboj kondenzátoru Q = I.t = C.U, odkud můžeme psát
Ze základů elektrotechniky je známo, že připojíme-li obvod RC na zdroj konstantního
napětí U, roste napětí na kondenzátoru exponencíálně, podle zákona
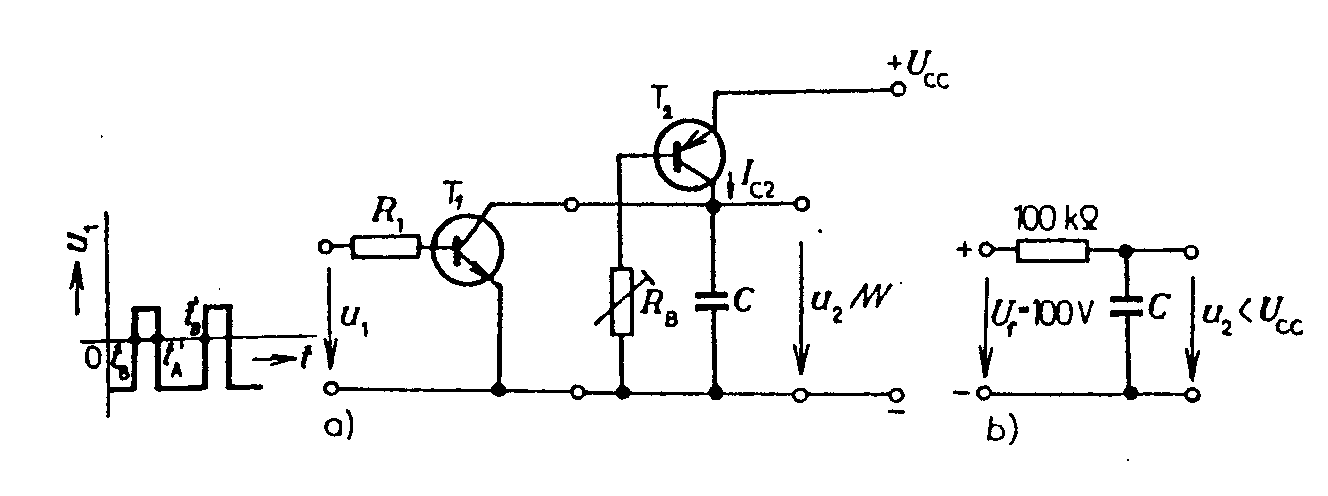
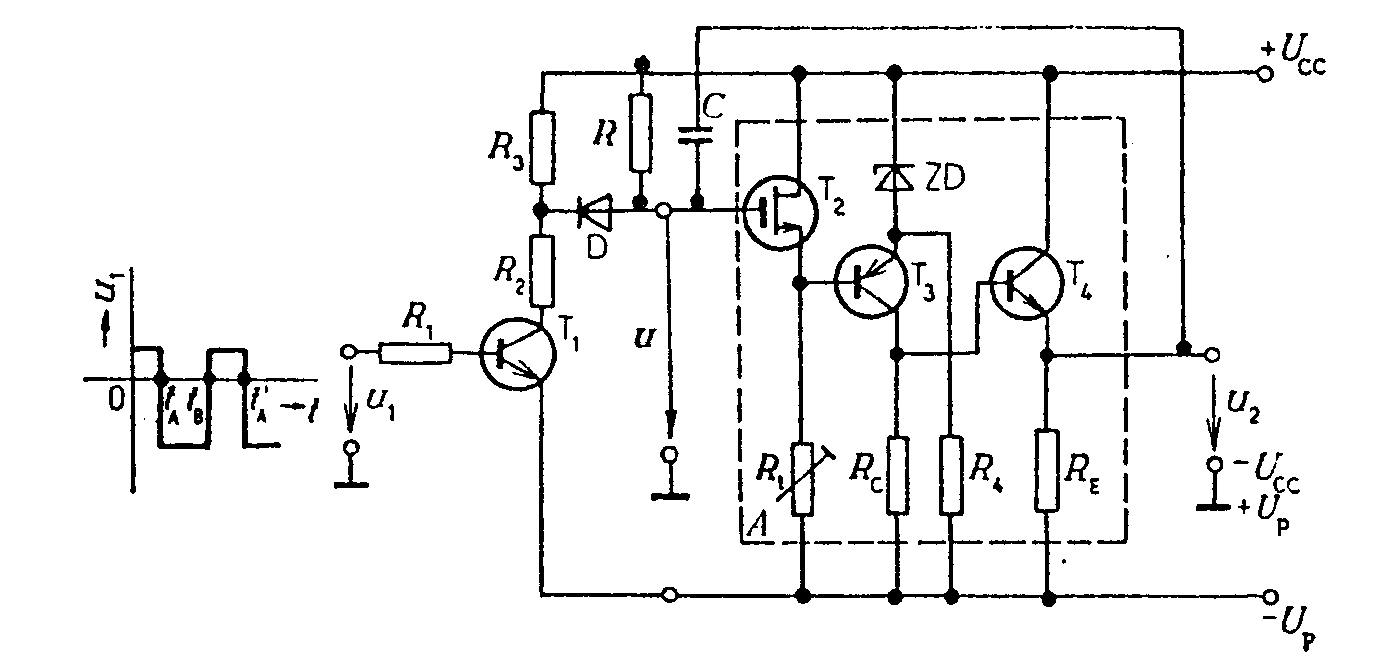
Vidíme, že b je tím menší, čím je větší časová konstanta obvodu RC. To lze docílit použitím dostatečně velkého ohmického odporu. Zvětšování kapacity kondenzátoru není vhodné, vzhledem k špatné kvalitě (velkému ztrátovému úhlu) kondenzátorů větších kapacit. Ovšem použití velkých pasivních odporů vyžaduje zvyšování napájecích napětí. Proto se v mnoha případech používá místo pasivního rezistoru dynamický odpor tranzistoru. Charakteristiky tranzistoru jsou uvedeny na obr. Pracujeme-li na charakteristice konstantního proudu do báze, je dynamický odpor tranzistoru dán hodnotou 1/h22e. Je-li např. dynamický odpor tranzistoru 1/h22e = 100kW a pracuje-li tranzistor s konstantním kolektorovým proudem IC = 1mA, je fiktivní napětí, ke kterému se blíží exponenciála Ufik = IC.1/h22e = 100.103 . 1.10-3 = 100V. Samozřejmě, i když exponenciála směřuje k napětí 100V, dojde k jejímu omezení po dosažení napájecího napětí tranzistoru u2 » UCC. Principielní schema zapojení je na obr.
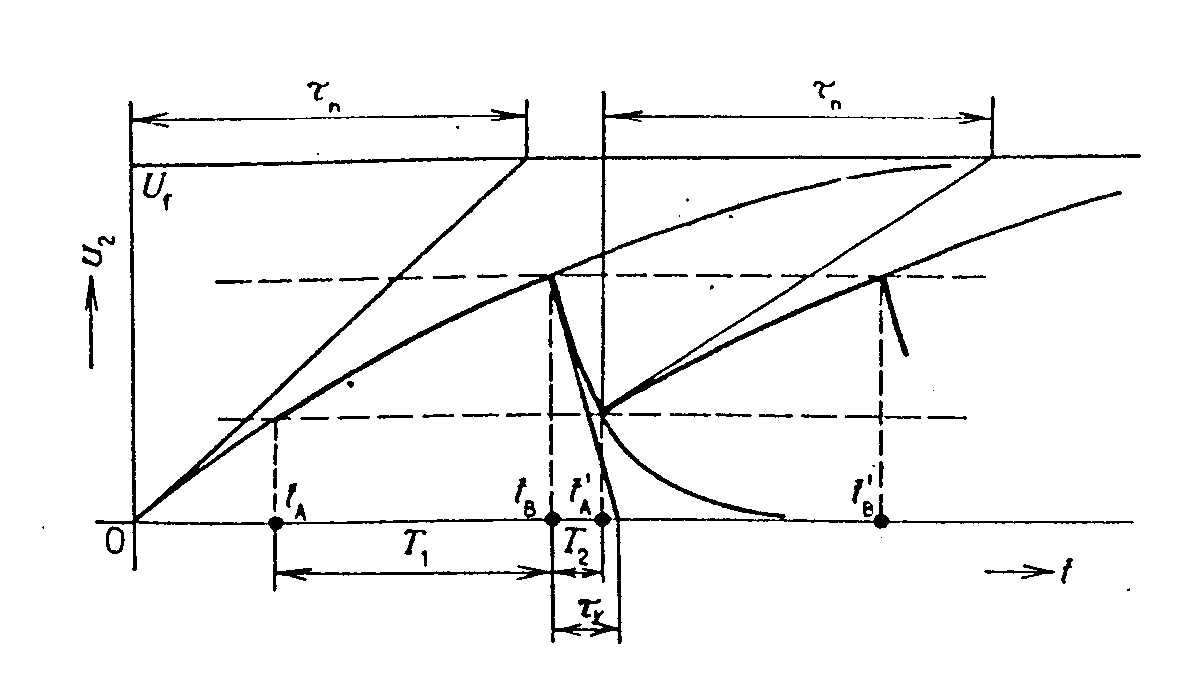
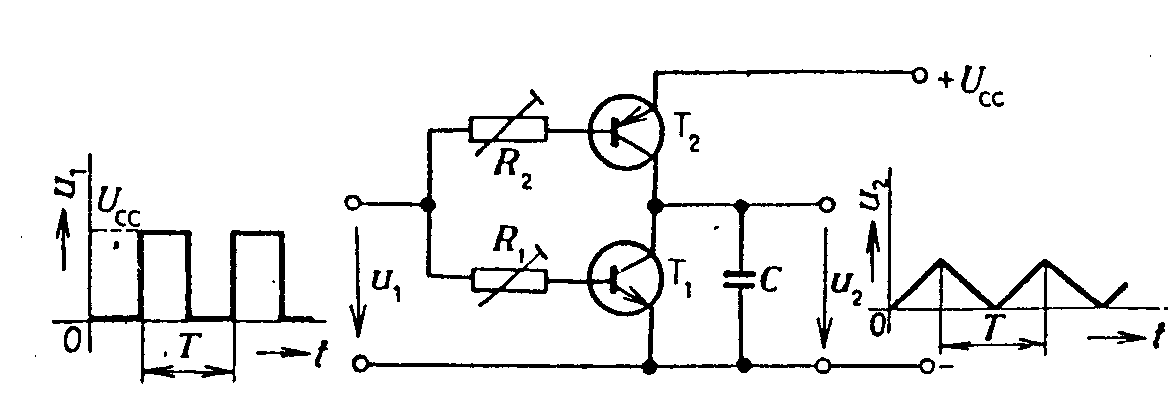
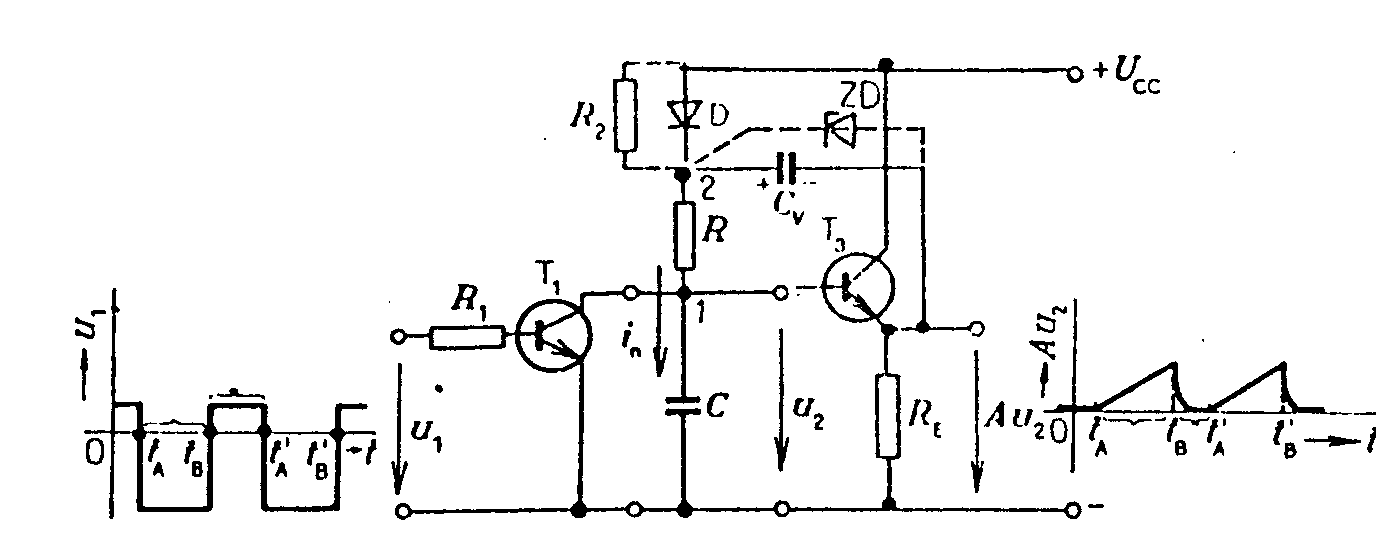
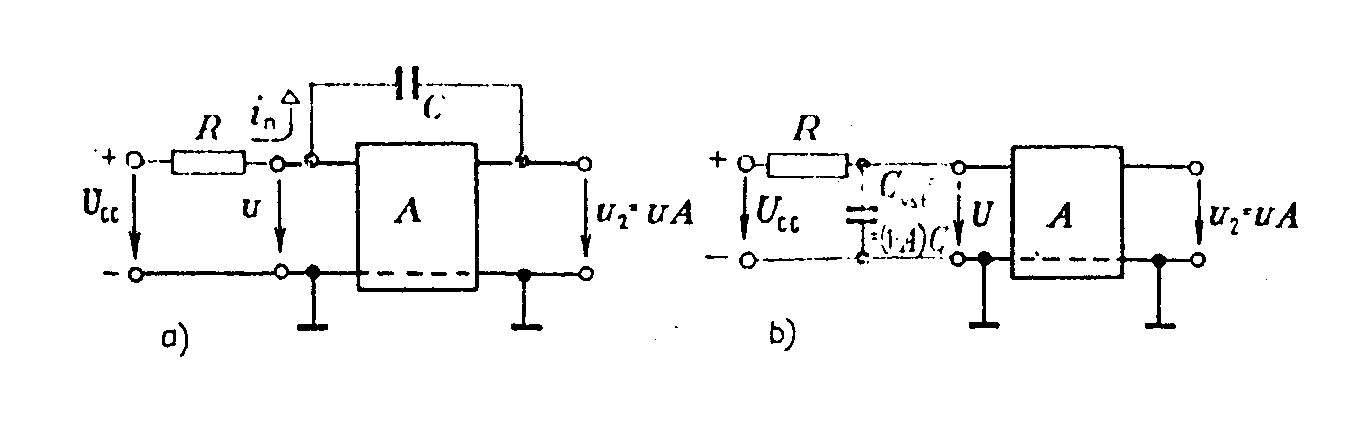
Průběh výstupního napětí je uveden na obr. Když se v čase tB otevře tranzistor T1 kladným obdélníkovým impulzem na bázi, vybije se kondenzátor C přes malý odpor otevřeného tranzistoru. Časová konstanta vybíjecího obvodu je malá. Po zavření tranzistoru T1 v čase ta¢, začne se kondenzátor nabíjet přes tranzistor T2 proudem, nastaveným odporem RB v bázi T2. Pracovní bod tranzistoru se pohybuje z bodu B do bodu A a kolektorový proud tranzistoru se téměř nemění. Použití dvou komplementárních tranzistorů umožní realizovat jednoduchý generátor trojúhelníkových průběhů. Schema zapojení je na obr. Při nulovém napětí u1 je tranzistor T1 zavřen a T2 otevřen. Přes T2 se nabíjí kondenzátor C proudem IC2, nastaveným odporem R2 v bázi T2. Při vstupním napětí u1 = UCC je T2 zavřen, T1 otevřen a kondenzátor C se vybíjí proudem, nastaveným odporem R1 v bázi T1. Kmitočet a amplitudu výstupního trojúhelníkového napětí lze regulovat nabíjecí a vybíjecí časovou konstantou obvodu a opakovací frekvencí a šířkou řídících impulzů u1. Linearizace pilových průběhů. Linearitu pilových průběhů ovlivňuje jednak okolnost, že nenabíjíme kondenzátor konstantním proudem a také zátěž, připojovaná na svorky generátoru pilových napětí. Čím je tato zátěž menší a čím menší část nabíjecí exponenciály využíváme, tím je linearity průběhu lepší. Problém linearizace výstupních průběhů lze řešit dvěma způsoby: a) Linearizace pomocí kladné zpětné vazby, t.zv. bootstrap Schema zappojení je na obr. Kondenzátor C je nabíjen v časovém intervalu tA, tB přes diodu D odpor R ze zdroje UCC. Tranzistor T1 je zavřen řídícím napětím u1 na bázi. Na kondenzátoru C vzrůstá výstupní napětí u2, které je současně přiváděno na vstup emitorového sledovače T3 s velkým vstupním odporem. Výstupní napětí sledovače Au2 je přiváděno přes velký kondenzátor Cv do bodu 2 mezi diodu D a odpor R. Napěťové zesílení sledovače A » 1. Jak se zvyšuje napětí na kondenzátoru u2, tak se zvyšuje napětí na výstupu sledovače Au2 a také napětí v bodě 2, takže napětí na rezistoru R zůstává konstantní. To znamená, že přes R teče konstantní proud, který nabíjí kondenzátor C. Po otevření tranzistoru T1 v čase tB se kondenzátor rychle vybije přes malý odpor otevřeného tranzistoru a po uzavření T1 v čase tA¢ se proces opakuje. Vazební kondenzátor Cv musí mít velkou kapacitu (např. 100mF). Je nabit na naznačenou polaritu na napětí UCC a ve zpětnovazebním obvodu působí jako zdroj konstantního napětí s velmi malým vnitřním odporem. V době přímého běhu pilového napětí na něm napětí poněkud poklesne a proto se musí před započetím dalšího přímého běhu počkat, až se jeho náboj doplní přes diodu D a emitorový odpor RE. Počítá se s mezerou mezi jednotlivými pilovými kmity asi 3RECv. Použije-li se místo kondenzátoru Cv Zenerova dioda ZD (spolu s odporem R2), potřeba mezery mezi pilovými kmity odpadá. Ovšem využití napájecího napětí je podstatně nižší, než v obvodu s kondenzátorem. Linearizace pilových průběhů pomocí záporné zpětné vazby. Druhou možností linearizace průběhu je zapojení pomocí t.zv. Millerova integrátoru. Princip zapojení je na obr. Kondenzátor C je zapojen v obvodu záporné zpětné vazby invertujícího zesilovače s velkým zesílením. Podle obr. se v důsledku Millerova jevu uplatní kapacita C jako fiktivní kapacita Cvst mezi vstupními svorkami zesilovače. Napětí na kondenzátoru je uC = u - u2 = uA - u = u(1-A). Nabíjecí proud kondenzátoru je vstupní impedance
zesilovače Jmenovatel (1-A) je reálné a kladné číslo. Zvst má kapacitní charakter. Má-li být Zvst menší (1-A) - krát, než XC, musí být Cvst = (1-A)C, přičemž výraz (1-A) může být 104 - 106. Tuto kapacitu je možno nabíjet ze zdroje UCC přes odpor R, přičemž napětí na kapacitě je (1-A)-krát zesilováno, takže využíváme jen malý úsek nabíjecí exponenciály a výstupní napětí je velmi lineární. Schema zapojení Millerova integrátoru je na obr. Třístupňový zesilovač má na vstupu unipolární tranzistor, což umožní použít velký odpor R a jakostní kondenzátor C s malou kapacitou. Rezistorem Rt v emitoru T2 se nastavuje takové napětí, že na kolektoru T3 je přibližně nulové napětí proti zemi. Tím je nulové napětí i na výstupu emitorového sledovače T4. Když se v čase tA zavře vstupním signálem tranzistor T1, zavře se i dioda D a kondenzátor C se začne nabíjet přes rezistor R ze zdroje UCC. Inverze signálu a velkého zesílení signálu je dosaženo ve stupni s tranzistorem T3. Nabíjení může probíhat až do uzavření tranzistoru T3. K tomu stačí jen několik desetin voltu na bázi T2. Tím bude změna napětí na R nepatrná a nabíjecí proud bude konstantní. Zpětný běh začne v okamžiku tB, když se T1 a D otevřou. Kondenzátor se přes ně vybije a na řídící elektrodě T2 se obnoví původní napětí. Zapojením lze realizovat dlouhé pilové impulzy, až několik minut. Ideálním zesilovačem pro Millerův integrátor jsou operační zesilovače, které mají zesílení 50 000 až 1 000 000 a s nimi se dosahují vynikající parametry integrátoru.
Generátory pilového proudu. Pro obrazovky s elektromagnetickým vychylováním požadujeme, aby proud ve vychylovacích cívkách měl lineární průběh. Předpoklájme, že na čistou indukčnost (bez ohmického odporu) připojíme elektrické napětí E ze zdroje konstantního napětí. Bude platit zákon
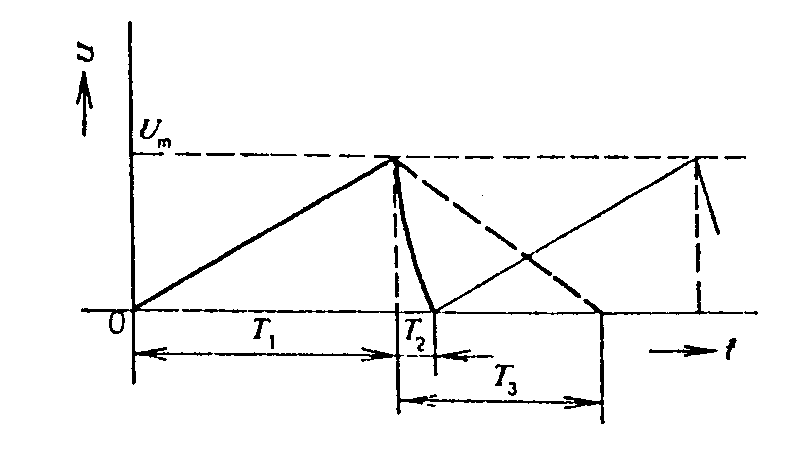
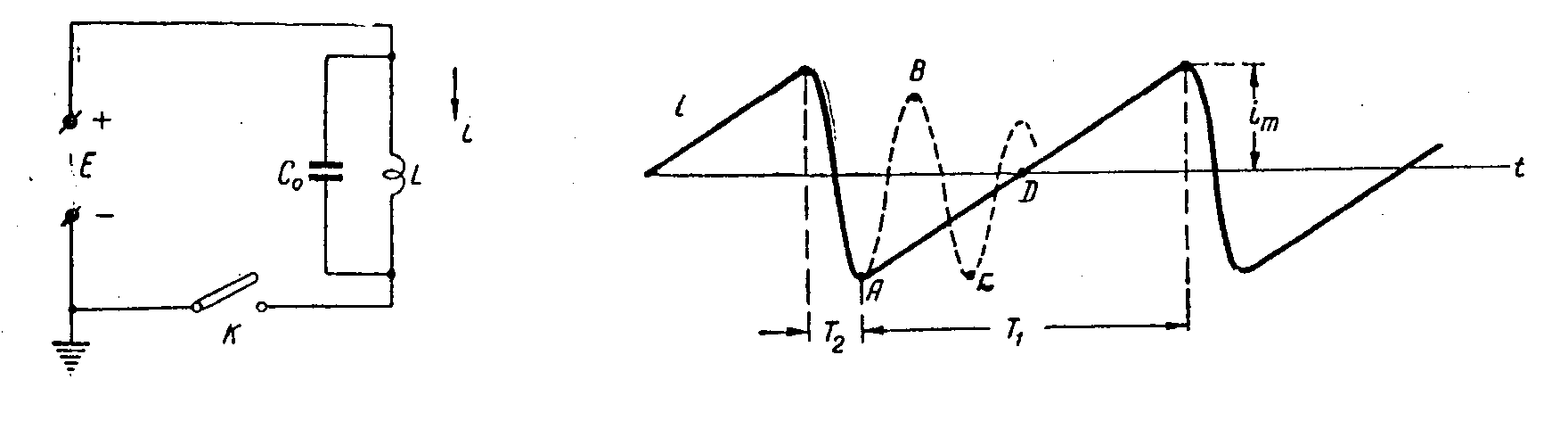
vidíme, že je-li hodnota E/L konstantní, bude proud v indukčnosti lineárně narůstat v čase. Požadujeme, aby proud ve vychylovacích cívkách měl průběh, zobrazený na obr. Mezi body A-B proud lineárně narůstá a mluvíme o přímém běhu T1. V intervalu B-A klesá proud z maximální hodnoty tm na minimální hodnotu -tm a mluvíme o zpětném běhu T2. Zatímco pro přímý běh požadujeme přísně lineární časovou závislost, pro průběh zpětného běhu neklademe žádné zvláštní požadavky na průběh, pouze jsou kladeny požadavky na dobu T2. Linearitu přímého běhu vyjadřujeme pomocí činitele nelinearity
Graficky je nelinearita znázorněna na obr. V rozkladových generátorech používáme pilové průběhy v cívkách horizontálního rozkladu a vertikálního rozkladu. Činitel nelinearity požadujeme pro horizontální cívky 10 ¸ 15%, pro vertikální rozklady 5¸8%. Předpokládejme obvod uvedený na obr. Cívka má indukčnost
L, ohmický odpor předpokládáme nulový, K cívce je vždy připojena parazitní
kapacita C0. V době přímého běhu se parazitní kapacita nemůže
uplatnit, obvod je zatlumen nulovým odporem R. Proud v indukčnosti lineárně
narůstá podle zákona Přímý běh zkončí rozepnutím klíče K na konci doby T1 a začne
zpětný běh. Napájecí zdroj se okamžitě odpojí a přestane tlumit obvod LC0,
který se rozkmitá na frekvenci, dané Thomsonovým vztahem Průběh je znázorněn body A-B-C-D. Proud v obvodu je i = im.cos wt a napětí na obvodu je
Po proběhnutí poloviny kmitu vlastních oscilací se opět klíč otevře a nulový odpor zdroje okamžitě zatlumí oscilace v obvodu. Zmíněnou polovinu kmitu vlastních oscilací použijeme jako dobu zpětného běhu, pokles amplitudy vlivem tlumení obvodu při zpětném běhu můžeme zanedbat. Doba zpětného běhu je tudíž dána vztahem
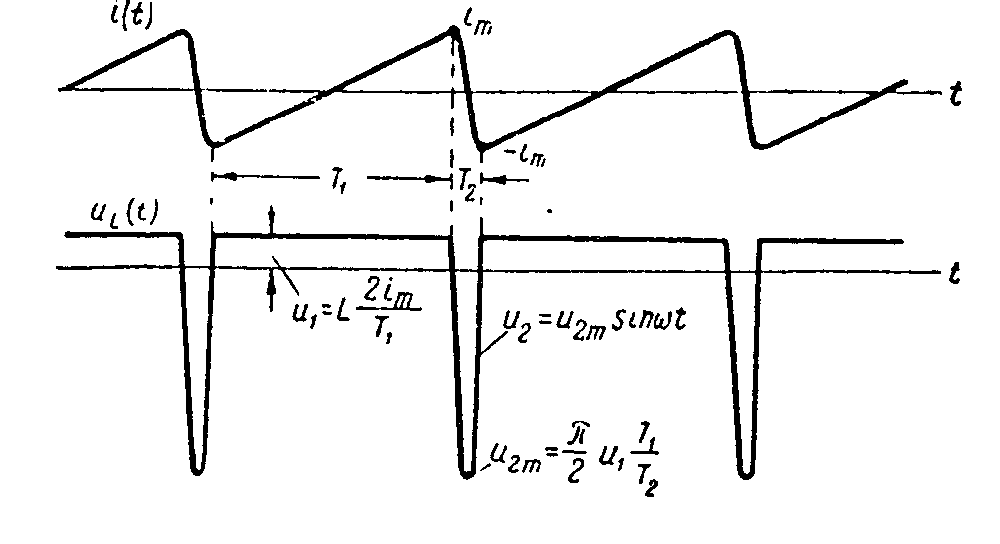
Amplituda napětí na indukčnosti při zpětném běhu je
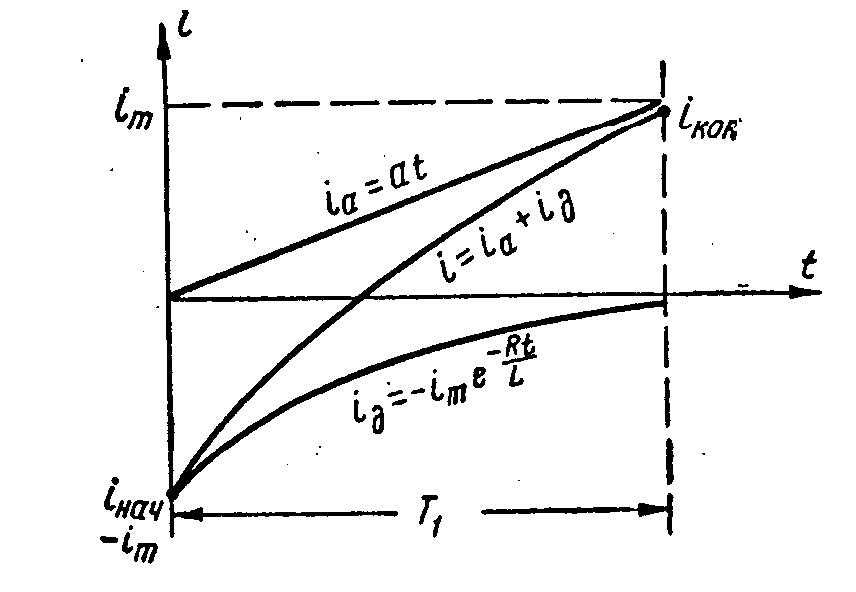
Průběhy napětí a proudů jsou uvedeny na obr.
Příklad. Předpokládejme, že L = 0,1H, T = T1+T2 = 64ms, T2 = 10%T1, im = 0,2A napětí pří přímém běhu amplituda napětí
při zpětném běhu maximální hodnota
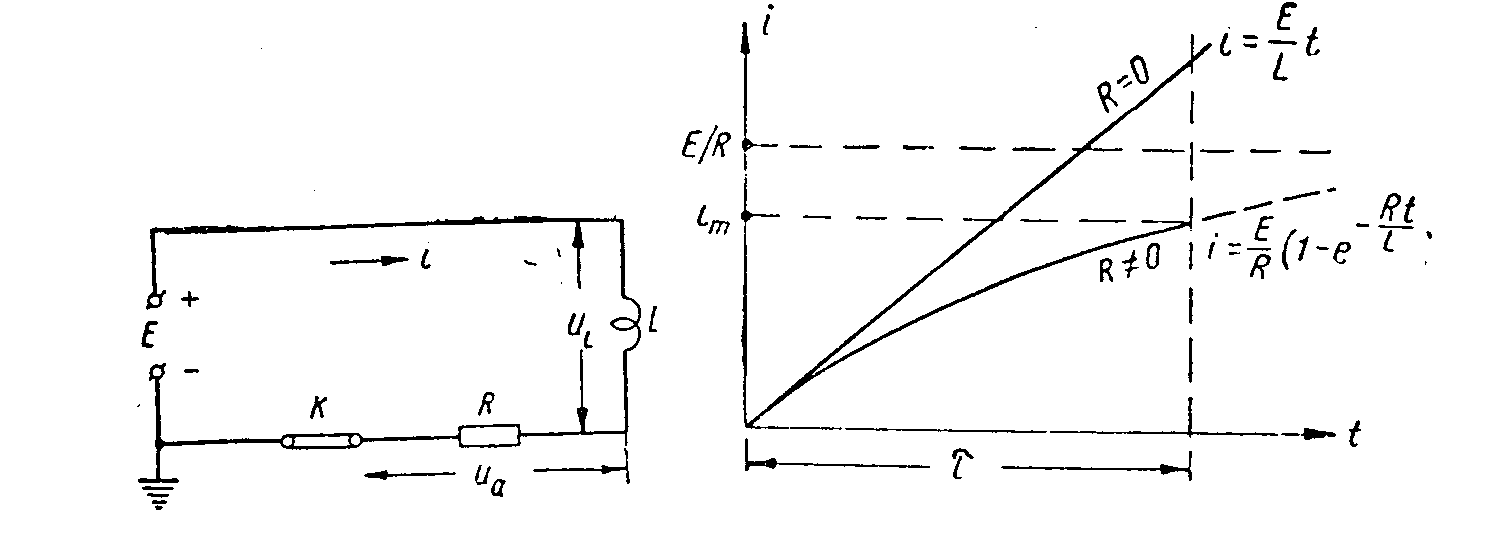
parazitní kapacity Vliv činného odporu. Ve skutečnosti každý obvod generátoru pilového proudu má vždy nenulový činný odpor, který je tvořen jednak ohmickým odporem cívky, odporem spínacího klíče, který je tvořen buď tranzistorem (nebo elektronkou), vnitřním odporem napájecího zdroje a odpory přívodů. Schema takového odporu je na obr. Při sepnutém
klíči platí rovnice, předpokládáme-li, že v čase t=0 je proud v obvodu
i=0 Pro proud tedy platí vztah
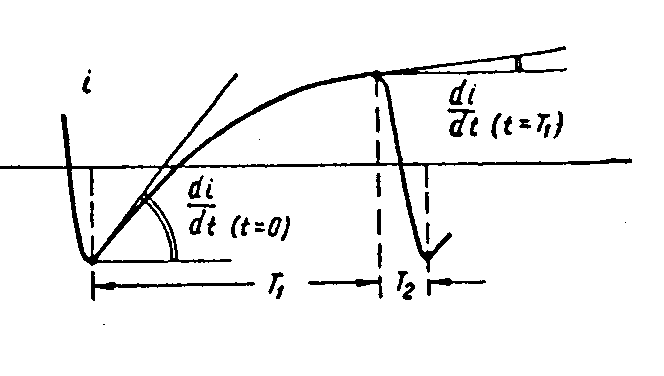
V grafu je vidět vliv činného odporu a pro činitel nelinearity platí
Zůstává otázka, je-li možno v obvodě, kde se vždy vyskytuje činný odpor přesto získat lineární průběh proudu. Sledujme možnost nahradit spínací klíč aktivním spínačem (tranzistorem nebo elektronkou). Předpokládejme, že převodní charakteristika aktivního spínače (t.j. závislost proudu ve výstupním obvodu na vstupním řídícím napětí) je uvedena an obr. Požadujme proud v obvodu i = at, kde a = konst. Platí tedy
Odtud
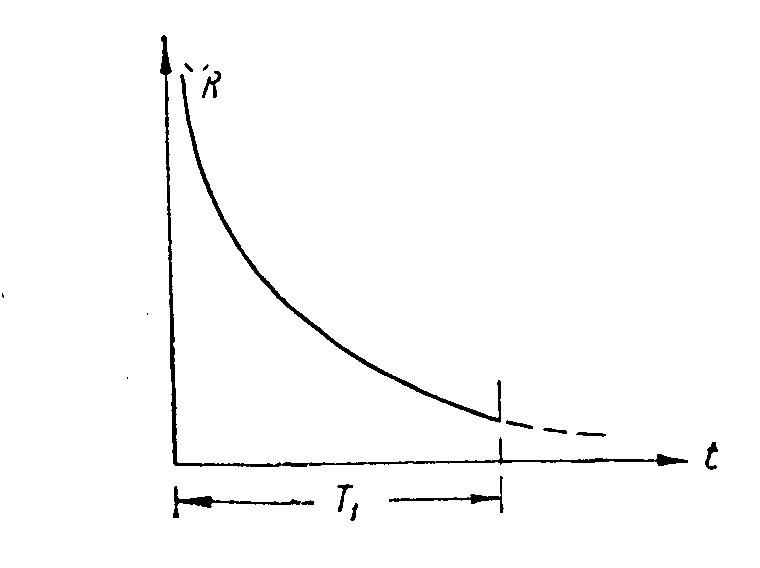
Závislost odporu na čase je na obr. Z přechodové charakteristiky lze psát pro výstupní proud
i0 je výstupní proud pří uC=0 Stejnosměrný odpor aktivního prvku
Porovnáme-li oba získané vztahy pro odpor, dostaneme S.uC + i0 = at a tedy řídící napětí aktivního prvku
Lze udělat závěr, že i v obvodech s indukčností a činným odporem lze generovat lineárně rostoucí proud, zajistíme-li, že ohmický odpor v obvodu je časově proměnný, a to tak, že s rostoucím časem odpor hyperbolicky klesá. Uvedené zapojení má ovšem nevýhodu, že na začátku přímého běhu je hodnota ohmického
odporu vysoká, obvod není tlumen a proto se na začátku přímého běhu superponují
na kmit pilového proudu sinusové oscilace, Tyto trvají až do doby (1/3 - 1/2
přímého běhu), než klesne hodnota ohmického odporu na hodnotu, při které přejdou
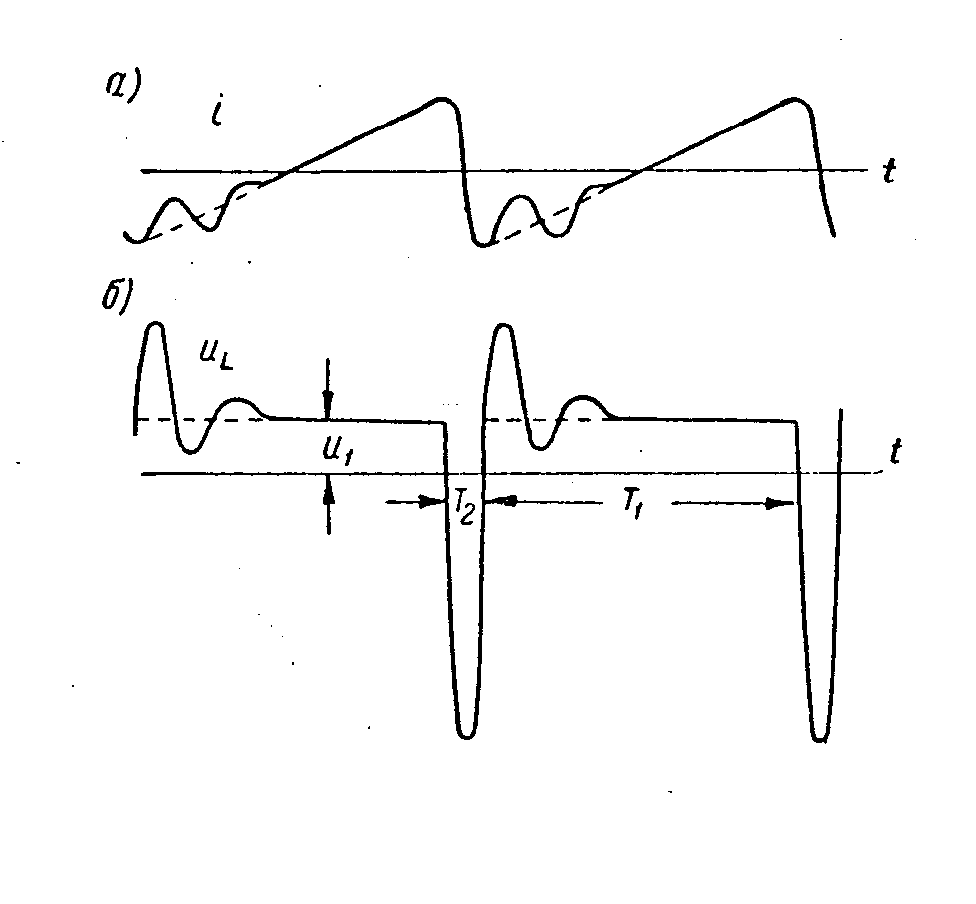
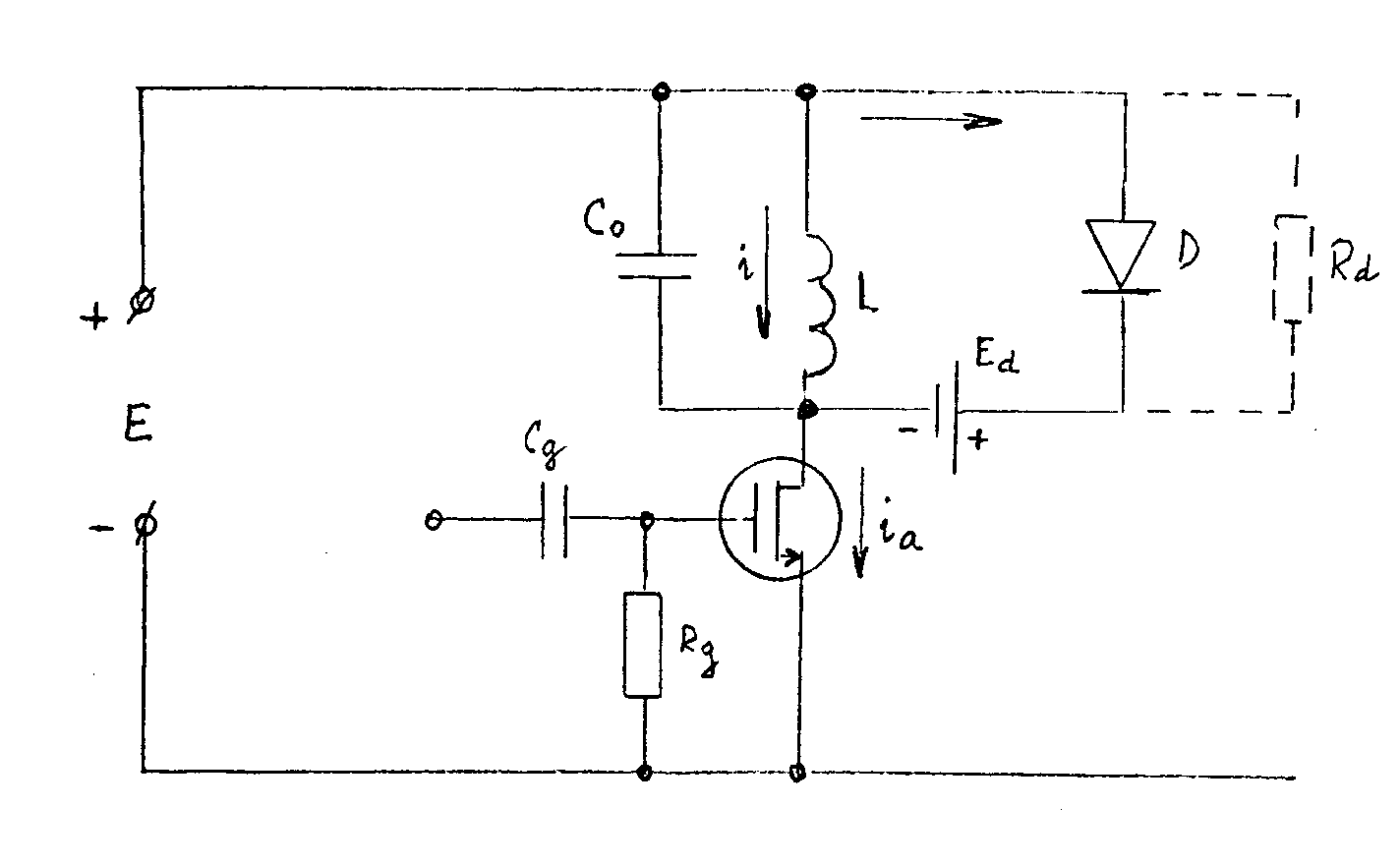
oscilace z kmitavého na aperiodický průběh, t.zn pod hodnotu Uvedený nedostatek se odstraňuje použitím tlumící diody. Principielní schema je uvedené na obr. Dioda je pomocí zdroje Ed polarizována v závěrném směru. Při prvním záporném kmitu se dioda otevře a svým malým odporem zatlumí oscilace. Napětí zdroje Ed se volí stejně veliké, jako je napětí na indukčnosti u1 při přímém běhu je připojeno záporným pólem na kolektor spínacího tranzistoru. Tlumící obvod je tvořen diodou D s odporem v přímém směru Rd, indukčností L a zdrojem Ed. Předpokládáme-li odpor diody pro jednoduchost lineární, platí následující vztahy pro objasnění průběhu proudů:
Vyloučením z rovnic proudu ia i id dostaneme následující diferenciální rovnici pro proud v indukčnosti
jejímž řešením je
Protože se napětí zdroje Ed volí vždy u1 = aL, je první člen v rovnici roven nule. Proto
Průběhy proudů jsou zobrazeny na obr. Počáteční a konečná hodnota proudu jsou v absolutní hodnotě stejné a rozkmit pilového proudu je im = aT1. Vypočítáme-li činitel nelinearity, dostaneme následující rovnici
Příklad. Předpokládáme-li L = 01H, Rd = 200W, T1 = 0,9T = 0,9.64.10-6 s, potom je Pro posouzení efektivnosti obvodu se nehodí koeficient účinnosti, který vyjadřuje poměr činného výkonu k celkovému výkonu, protože vychylování elektronového paprsku magnetickým polem je pouze čistě reakční proces, který žádný činný výkon nepotřebuje. (Pokud se objevuje v těchto obvodech ztrátový výkon, vyjadřuje pouze nedokonalost návrhu samotného obvodu). Zde se posuzuje efektivnost jako poměr maximálního proudu k jeho střední hodnotě. Uvážíme-li průběh prouhu spínacím prvkem podle obr. a zanedbáme-li dobu zpětného běhu, je střední proud
Efektivnost obvodu je
V ideálně ekonomicky pracujícím obvodu je g = ¥. Zapojení, které bylo principielně popsáno, se používá pouze u malých obrazovek. Zde spínací tranzistor i tlumící dioda pracovaly po celou dobu přímého běhu. Obvod má analogii s dvojčinným zesilovačem pracujícím ve třídě A. Moderní obvody používají zdokonalené zapojení, v kterém v první polovině přímého běhu pracuje pouze tlumící dioda a ve druhé polovině pracuje pouze spínací tranzistor. To má analogii s dvojčinným zesilovačem, pracujícím ve třídě B. Ekonomika činnosti těchto zapojení je přibližně dvojnásobná. Dělení : 1) Generátory s pilovým průběhem 2) Generátory s trojúhelníkovým průběhem - proud s pilovým průběhem se využívá v obrazovkách televizorů - napětí s pilovým průběhem má využití v osciloskopických obrazovkách - rozkladové generátory - generátory časové základny Požadavek linearity pro přímý i zpětný běh Požadavek linearity pouze pro zpětný běh - doba zpětného běhu co nejkratší - nastavitelná amplituda a snadná synchronizace Principy : Napětí pilového průběhu dostaneme při nabíjení kondenzátoru
|
|
zpět na předchozí stránku
Copyright © 2003 Hell
doporučené rozlišení 1024x768

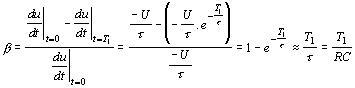 pro T1/
pro T1/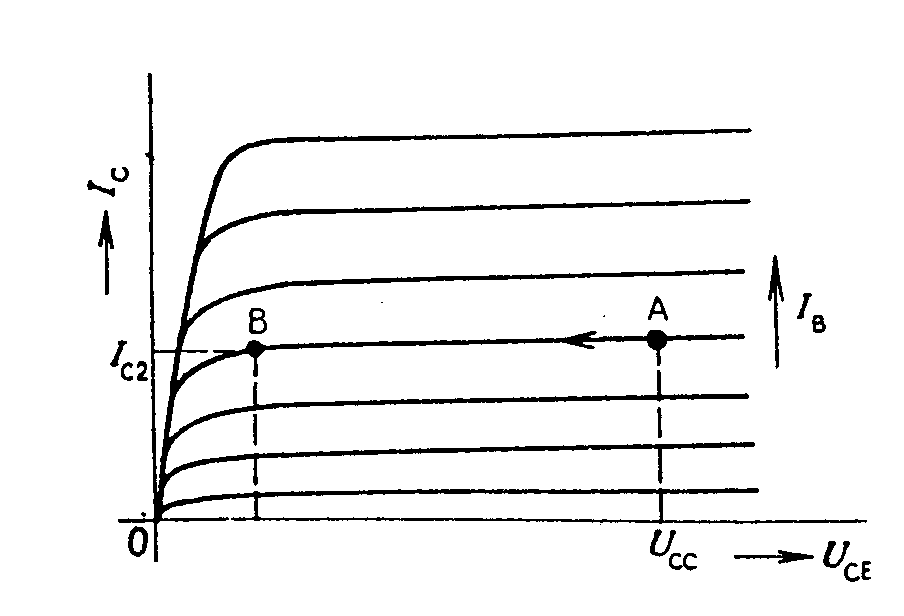
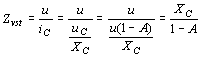
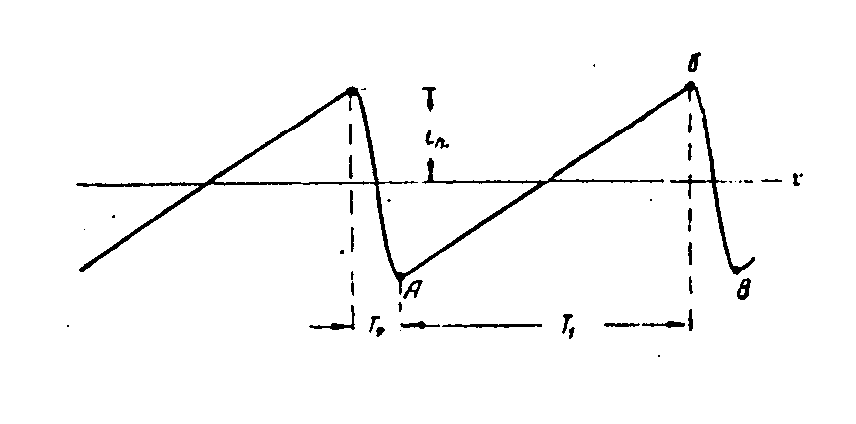
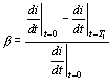
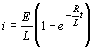
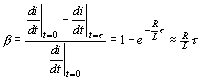 pro
pro