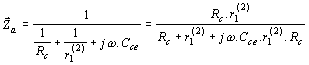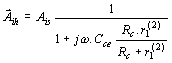|
|
HŘÍŠNÍCI NOVÝ UŽIVATEL nepřihlášený uživatel Právě si tyto stránky čte 1 člověk. |
|
Poslední změna:
29.09.2007 |
|
Návštěvník číslo: 26434 |
| ICQ:61783389 |
|
Copyright © 2003 Hell |
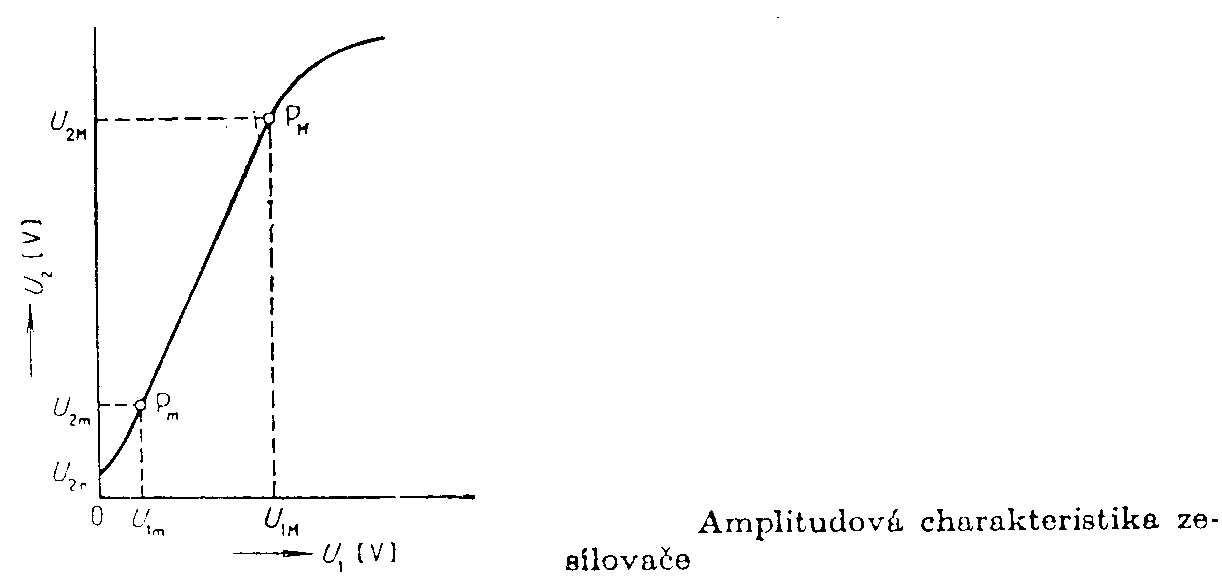
Elektornika II.Dokumenty a příkladyZesilovače I.VOŠ a SPŠE PLZEŇ, ZESILOVAČE I., Učební texty Zesilovače I. Zesilovače jsou elektrická zařízení, která slouží k zesilování a úpravě elektrických signálů. Patří do kategorie dvojbranů, t.j. obvodů, které mají dvě vstupní a dvě výstupní svorky. Z elektrotechnického hlediska můžeme dělit zesilovače podle různých hledisek. podle použitého zesilovacího prvku se dělí na zesilovače : - tranzistorové - elektronkové - magnetické - parametrické a pod. podle velikosti budícího signálu dělíme zesilovače na: - zesilovače velkých signálů - zesilovače malých signálů - zesilovače velmi malých signálů podle druhu budícího signále se dělí na zesilovače: - nízkofrekvenční - používají se převážně v akustické technice - vysokofrekvenční - vyskytují se prakticky v každém zařízení pro zpracování radiotechnických signálů - impulzové - pro zpracovávání radiolaokačních nebo televizních signálů -zesilovače stejnosměrné - vyskytují se v lékařských, měřících a regulačních obvodech podle šířky přenášeného pásma dělíme zesilovače na : - úzkopásmové - třídecibelová šířka přenášeného kmitočtového pásma (B3) činí několik procent středního kmitočtu f0. širokopásmové - třídecibelová šířka přenášeného pásma je srovnatelná se středním kmitočtem f0. podle polohy pracovního bodu rozeznáváme zesilovače třídy: A - výstupní proud teče v zesilovacím prvku po celou periodu signálu - říkáme, že úhel otevření a0 = 2p B - výstupní proud teče v zesilovacím prvku po dobu půl periody, t.zn., že úhel otevření a0 = p C - výstupní proud teče v zesilovacím prvku po dobu menší, než je půl periody, t.zn. že a0 < p. třída A třída B třída C podle zapojení zesilovacího prvku - rozeznáváme zesilovače a) se společným emitorem (SE) b) společným kolektorem (SC) c) společnou bází (SB) SE SC SB Podobné zapojení mají i zesilovače s unipolárními tranzistory nebo elektronkami. podle způsobu činnosti dělíme zesilovače na a) jednočinné b) dvojčinné podle vazby mezi stupni dělíme zesilovače na zesilovače s a) kapacitní vazbou b) přímou (galvanickou) vazbou c) transformátorovou vazbou Základní parametry zesilovačů. Amplitudové charakteristiky mají obvykle průběh, znázorněný na obr. Charakteristika platí pro sinusový signál o jednom kmitočtu. Nulovému vstupnímu napětí odpovídá nenulové napětí na výstupu. Toto nežádoucí rušivé napětí U2r má charakter šumu nebo brumu, jeho původ je v nedokonalosti zesilovače a omezuje nám jeho použitelnost. Čím větší jsou nároky na kvalitu zesilovače, tím musí být větší odstup užitečného signálu od rušivého. Např. amplituda výstupního napětí U2M musí být 10 x větší, než amplituda U2r. Má-li zesilovač pracovat jako lineární čtyřpól, nesmí pracovní oblast na jeho amplitudové charakteristice vybočit z lineární oblasti. Činitel napěťového zesílení - Zisk zesilovače je vyjádřením napěťového zesílení
v dB, tedy Mají-li vstupní a výstupní veličiny sinusový průběh,
ale různou fázi, zavádí se pojem komplexní amplitudy střídavého napětí
Analogicky platí i pro proudový zesilovací činitel
Na základě Ohmova zákona lze proudy signálů vyjádřit
odpovídajícími hodnotami napětí a impedancí a získat vztah mezi napěťovým a
proudovým zesílením Výkonové zesílení se udává jako poměr činného výkonu, dodávaného do zátěže k činnému výkonu, dodávanému zdrojem budícího signálu. Činný výkon dodávaný do zátěže lze vyjádřit jako
Dosazením výše uvedených vztahů pro výkonové zesílení
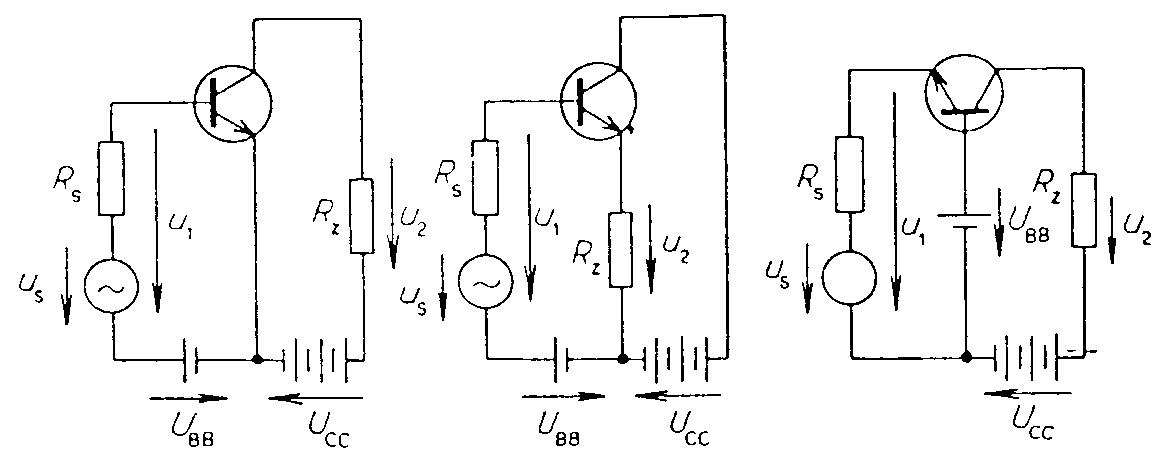
dostaneme vztahy Výkonový zisk je výkonové zesílení, vyjádřené v dB a platí vztahy Vstupní a výstupní impedance zesilovače jsou pasivní prvky náhradních schémat zesilovače, dle obr. Aktivní prvky v náhradních schématech U20 a I20 jsou ideální zdroje, závislé na budícím signálu. Uvedená schemata jsou rovnocenná a platí, že Z1 = Zvst, Z2 = Zvýst. Nelineární zkreslení. Budí-li se zesilovač sinusovým signálem, není průběh výstupního signálu čistě sinusový. Provede-li se harmonická analýza výstupního napětí zesilovače, buzeného vstupním signálem o frekvenci f, získá se základní harmonická složka výstupního napětí s amplitudou Uf a vyšší harmonické s amplitudami U2f, U3f, atd. Velikost nelineárního zkreslení se vyjadřuje činitelem harmonického zkreslení k podle vztahu Činitel harmonického zkreslení je závislý na vybuzení zesilovače. Nejpřísnější požadavky na zkreslení bývají u zesilovačů akustických signálů, protože zde i malá změna obsahu harmonických složek působí rušivě. U jakostních signálů se požaduje, aby činitel harmonického zkreslení byl menší než 1%. Zesilovače jsou často buzeny více sinusovými signály současně. Potom vzniká v zesilovačích větší množství nežádoucích kmitočtových složek. Vedle harmonických složek jednotlivých sinusových signálů vznikají vlivem nelinearit charakteristik také další nežádoucí složky signálu, jejichž kmitočty jsou dány kombinacemi součtových a rozdílových kmitočtů vstupních signálů a jejich harmonických složek. Tomuto zkreslení říkáme intermodulační zkreslení a určuje se měřením pro které je normou ČSN 367420 stanovena velikost kmitočtů a amplitud měrných vstupních signálů. Produkty intermodulačního zkreslení nemají přímý vztah k vstupnímu signálu a proto působí mnohem rušivěji, než složky harnonické. Ovšem měření intermodulačního zkreslení je mnohem obtížnější, proto se udává jen v závažných případech. U kvalitních zesilovačů se toleruje do 3%, t.j. do trojnásobku přípustné hodnoty harmonického zkreslení. Vyšetřování činitele nelineárního zkreslení. Předpokládejme, že převodní funkce i2
= f(u1) je vyjádřena jednoduchou křivkou, kterou lze analyticky vyjádřit
interpolačním polynomem takže interpolační polynom lze převést na řadu Jak je známo, k určení polynomu n-tého stupně je třeba zjistit (n+1) pořadnic sledované křivky. Je výhodné používat lichý počet funkčních hodnot. Proto se používá tří, pěti nebo sedmibodová metoda k určení zkreslení. Obecně tříbodovou metodou určíme 1. a 2. harmonickou, pětibodovou metodou určíme přesně 1. a 2. harmonickou, s menší přesností už 3. a 4. harmonickou. Dynamickou převodní charakteristiku lze nahradit s určitou přesností kvadratickou parabolou (je-li zatěžovací odpor dostatečně malý a pracovní bod nezasahuje do oblasti výstupních charakteristik, kde jsou tyto značně zakřiveny).
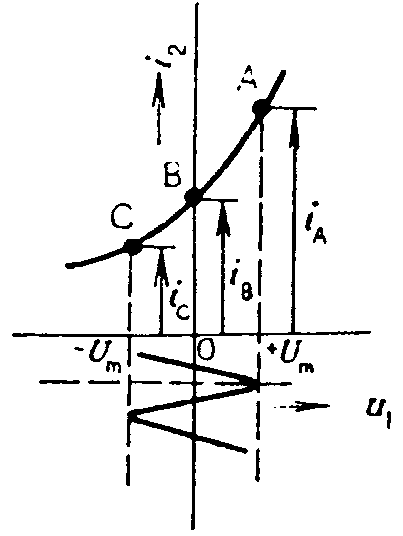
V případě tříbodové metody platí rovnice V případě pětibodové metody platí rovnice
Příklad: Pomocí tříbodové metody určit proudy I0m, I1m a I2m, bylo-li odečtěno z převodní charakteristiky: iA = 36 mA, iB = 16 mA, iC = 4 mA. Činitel nelineárního zkreslení Kolektorový proud je dán rovnicí Kmitočtové charakteristiky. Názornou představu o základních vlastnostech zesilovače
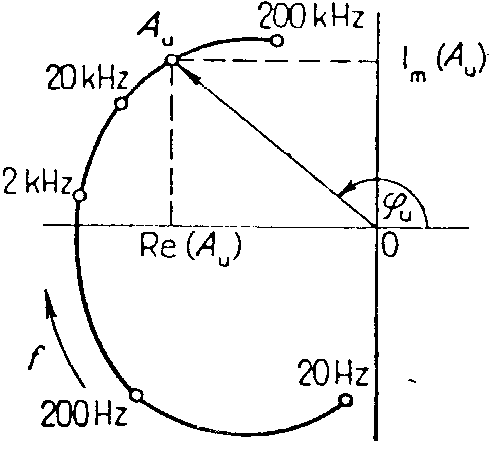
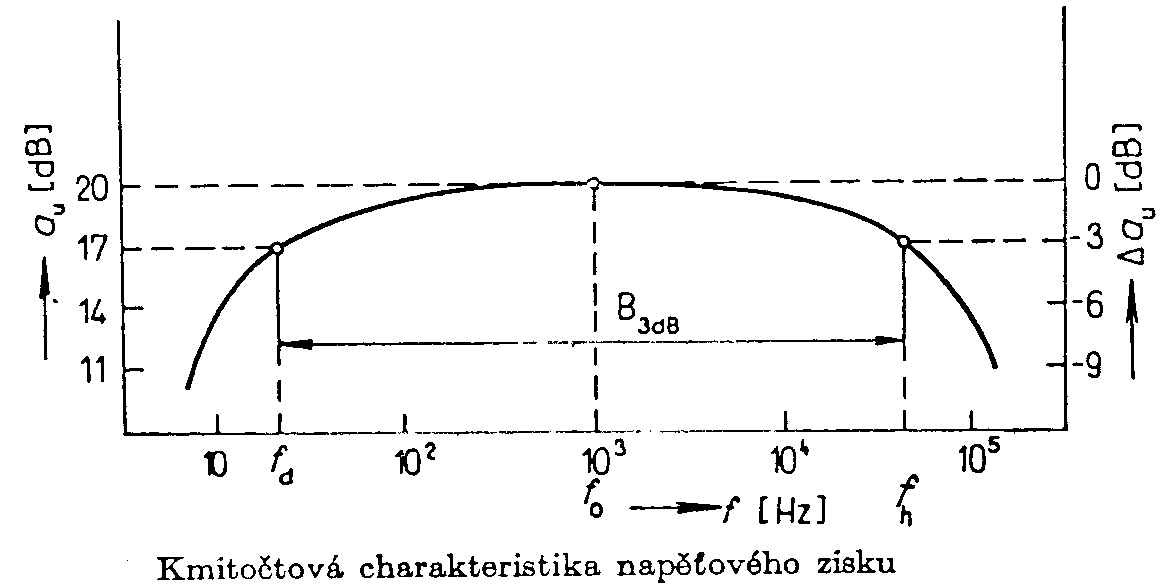
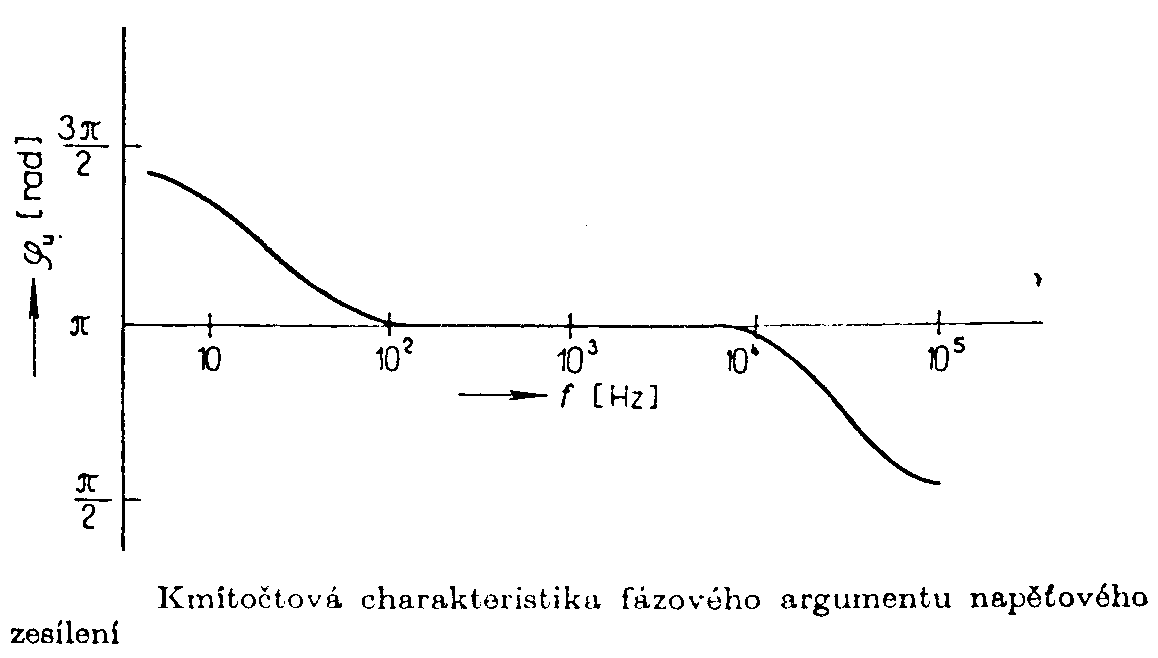
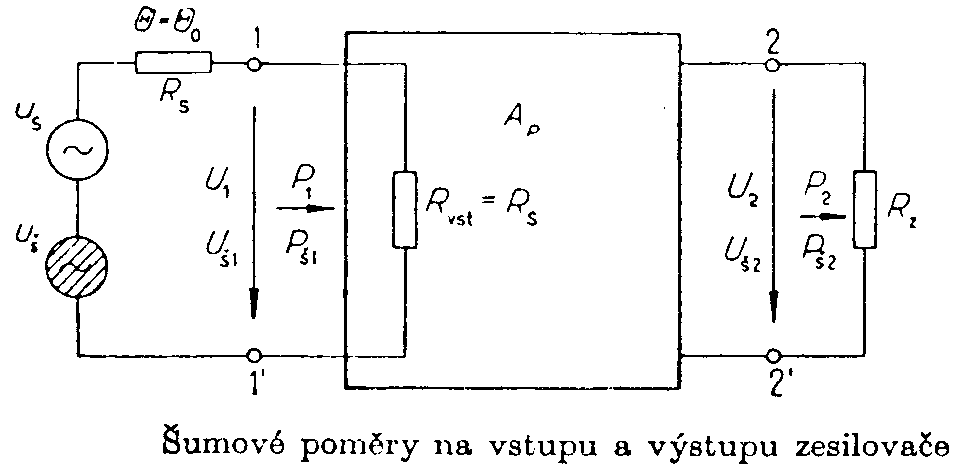
poskytuje kmitočtová charakteristika komplexního zesílení Mezi komplexním napěťovým zesílením a jeho složkami platí vztahy: V pravoúhlé soustavě se vynáší zpravidla kmitočet na vodorovnou osu v logaritmickém měřítku a zesílení na vertikální osu v dB. Šířka pásma je obor kmitočtů, v kterém je absolutní hodnota odchylek zisku menší než 3 dB. Tento obor je na straně nižších kmitičtů vymezen t.zv.dolním mezním kmitočtem fd a na straně vyšších kmitočtů t.zv. horním mezním kmitočtem fh. V pravoúhlých souřadnicích se zobrazuje také kmitočtová závislost fázového argumentu ju = f(ju) a nazývá se fázová charakteristika daného zesilovače nebo zkráceně fázová charakteristika. Podle průběhu kmitočtových charakteristik lze posoudit, do jaké míry zesilovač vyhovuje danému použití. Nemá-li zesilovač zkreslovat, musí být splněny následující podmínky: a) výstupní signál smí obsahovat jen ty harmonické složky, které jsou ve vstupním signálu (t.j. činitel harmonického zkreslení je v celém rozsahu přenášených kmitočtů a výstupních výkonů roven nule). b) na výstupu musí být všechny harmonické složky, které jsou ve vstupním signálu (t.j. zesilovač vykazuje v celém rozsahu přenášených kmitočtů co nejmenší odchylky zisku). Typický průběh fázové charakteristiky je na obr. Přenášené pásmo kmitočtů je od 102 do 104 Hz. V tomto frekvenčním pásmu mívá zesilovač stálý zisk, roven celistvému násobku p. Naopak v kmitočtových oblastech, kde se mění zisk zesilovače nastává i změna fázového argumentu, způsobujícího fázové zkreslení. T.zn., že i z průběhu ziskové charakteristiky lze soudit na průběh fázového zkreslení. Přechodová charakteristika. Jakost zesilovačů lze také posuzovat podle průběhu t.zv. přechodové charakteristiky, což je odezva zesilovače na jednotkový skok vstupního signálu u1(t). Zobrazuje se v pravuůhlých souřadnicích. Přechodové charakteristiky mohou mít buď monotónní průběh, nebo mohou vykazovat překmity, viz obr. Čím více se průběh přechodové charakteristiky podobá vstupnímu skoku, tím je zesilovač jakostnější. Průběh přechodové charakteristiky je dán obvodovými prvky L,R,C daného zesilovače. Z průběhu kmitočtové charakteristiky lze metodami vyšší matematiky získat přechodovou charakteristiku a naopak. Tato možnost se využívá převážně při analýze a syntéze zesilovačů, určených pro impulzní signály. Šumové vlastnosti. Každý zesilovač má na výstupu signály, které nesouvisí s budícím signálem. Jsou to rušivá napětí, neboť vytváří nežádoucí hluk v pozadí užitečného signálu. Tato rušivá napětí jsou dvojího druhu: - brumová napětí - která mají kmitočet rovný kmitočtu síťového napájení nebo jeho celistvým násobkům. Vznikají obvykle nedokonalým odstíněním nebo filtrací napájecích napětí nebo elektromagnetických polí síťových transformátorů. - šumová napětí - jsou napětí s nahodile proměnným průběhem. Tato tvoří soubor velkého množství střídavých složek všech možných kmitočtů. Jejich původ je v ohmických rezistorech a v aktivních prvcích zesilovačů. Brumová napětí lze potlačit dokonalou filtrací napájecích napětí a vhodnou konstrukcí s použitím stínících krytů. Šumová napětí lze potlačit mnohem obtížněji, zejména u zesilovačů s velkým zesílením a velkou šířkou přenášeného pásma. Šumové poměry na vstupu zesilovače jsou vyznačeny na obr. Zdroj budícího napětí s vnitřním odporem Rs produkuje nejen užitečný signál US, ale také šumové napětí s efektivní hodnotou UŠ.Pro srovnávání šumových vlastností zesilovačů jsou stanoveny t.zv. normální šumové podmínky: a) Šumové napětí UŠ je tepelné šumové napětí vznikající na vnitřním odporu zesilovače při šumové teplotě Q0=290K. b) Vstupní odpor zesilovače je roven vnitřnímu odporu zdroje (Rvst = RS). Pro výpočet efektivní hodnoty tepelného šumu platí
vztah kde k = 1,38.10-23 J/K je Bolzmanova konstanta Q0 je šumová teplota odporu RS v kelvinech Df je šumová šířka přenášeného pásma. Přibližně se rovná B3dB zesilovače Při výkonovém přizpůsobení budícího generátoru a vstupu zesilovače se na vstupní svorky zesilovače přivádí napětí UŠ1 = UŠ/2, jemuž odpovídá výkon, dodávaný do zesilovače Vztah mezi vstupním a výstupním výkonem užitečného
signálu je Ideální zesilovač, který by neobsahoval žádný zdroj šumu by produkoval na výstupu šumový výkon Pš2i, rovněž Ap krát větší, než je šumový výkon, přiváděný na vstup Pš2i = ApPš1. Každý reálný zesilovač ale obsahuje řadu zdrojů šumu (rezistory, tranzistory a p.), takže jeho výstupní šumový výkon je větší, než u ideálního zesilovače.Proto můžeme psát Pš2 = F.Pš2i = F.Ap.Pš1. Koeficient F vyjadřuje šumové vlastnosti zesilovače a nazývá se šumový součinitel daného zesilovače za normálních šumových podmínek. Ideální nešumový zesilovač by měl F=1. Udává tedy šumový činitel, kolikrát je šumový výkon na výstupu reálného zesilovače větší, než by byl v případě, kdyby zesilovač neobsahoval žádný zdroj šumu. Šumový činitel lze definovat i jinak. Vlastní šum zesilovače způsobuje, že odstup signál/šum je na výstupu vždy menší než na jeho vstupu. Proto platí nerovnost Dosadíme-li za jednotlivé výkony, shledáme, že tento podíl výkonových poměrů signálu k šumu na vstupu a výstupu se rovná šumovému činiteli F Šumový činitel tedy udává, kolikrát je poměr signál/šum na vstupu zesilovače větší než na jeho výstupu. Dělíme-li šumový výkon na výstupu zesilovače jeho
výkonovým zesílením, získáme šumový výkon, který je nutno přivést na vstup nešumícího
zesilovače s jinak stejnými vlastnostmi, aby zůstaly šumové poměry na výstupu
nezměněny. Poměr tohoto výstupního šumového výkonu přepočítaného na vstup
Výstupní šumový výkon přepočítaný na vstup zesilovače
Poměr šumových výkonů Při normálních podmínkách je na vstup zesilovače
dodáván šumový výkon Šumové vlastnosti lze také vyjádřit t.zv. šumovou
teplotou zesilovače Qv. Rovná se teplotě
odporu RS při které by by dodával na vstup zesilovače právě šumový
výkon Má-li například zesilovač vlastní šumovou teplotu
QV = 1450K, je jeho vlastní šumový činitel Šumový činitel vyjádřený v dB se nazývá šumové
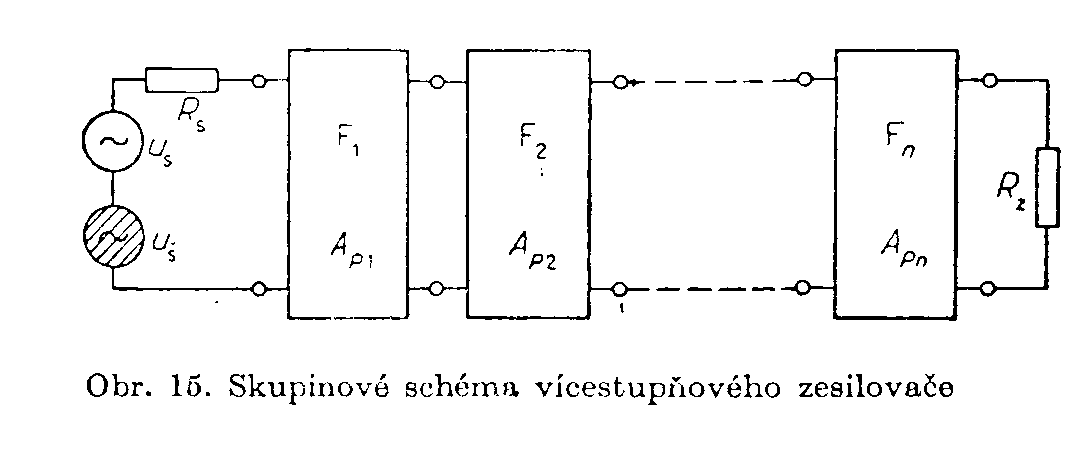
číslo zesilovače. V daném případě je Zesilovače jsou zpravidla složeny z většího počtu zesilovacích stupňů zařazených za sebou. Ze známých šumových činitelů F1, F2, ...FN a výkonových zesílení AP1, AP2, ....APN jednotlivých stupňů se určí šumový činitel celého zesilovače podle Friisova vzorce Z toho plyne důležitý závěr: Je-li výkonové zesílení prvního stupně dostatečně velké, je šumový činitel celého zesilovače roven šumovému činiteli prvního stupně (F » F1). Je to v souladu s fyzikálním názorem, podle kterého má rozhodující vliv na poměr signál/šum první stupeň, na jehož vstup přichází signál s nejmenší úrovní. Je-li známý šumový činitel zesilovače, lze pro daný poměr signál/šum na jeho vstupu vypočítat poměr signál/šum na výstupu. Šumové vlastnosti zesilovačů se často vyjadřují
prahovou citlivostí. Je dána napětím užitečného signálu US,
při kterém se získá na výstupu zesilovače požadovaný odstup signál/šum na výstupu
(U2/Uš2). Vztah mezi prahovou citlivostí zesilovače a
jeho šumovým činitelem se získá po dosazení poměru druhých mocnin napětí do
definičního vzorce šumového činitele Při normálních šumových podmínkách je šumové napětí
Prahová citlivost je tím větší, (t.j.potřebné napětí
signálu U1 tím menší), čím je menší šumová šířka pásma Df,
vnitřní odpor generátoru RS, šumový činitel F a čím se požaduje menší
poměr signál/šum na výstupu zesilovače. Např. pro Df = 9 kHz, RS
= 1 kW, F = 6, U2/Uš2 = 20 je prahová citlivost
zesilovače Nejsou-li splněny normální šumové podmínky zesilovače
tím, že na vstup nepřichází normální šumový výkon Reálný šumový činitel se taky někdy liší od normálního, není-li dodrženo výkonové přizpůsobení mezi budícím generátorem a vstupem zesilovače, nebo je-li vstupní odpor zesilovače odlišný pro užitečný signál a pro šum. Nedodržení přizpůsobení ale nemusí vždy vést k zvětšení šumu. Existuje t.zv. šumové přizpůsobení vstupu, při kterém je šumové číslo menší oproti výkonovému přizpůsobení až o 3 dB.
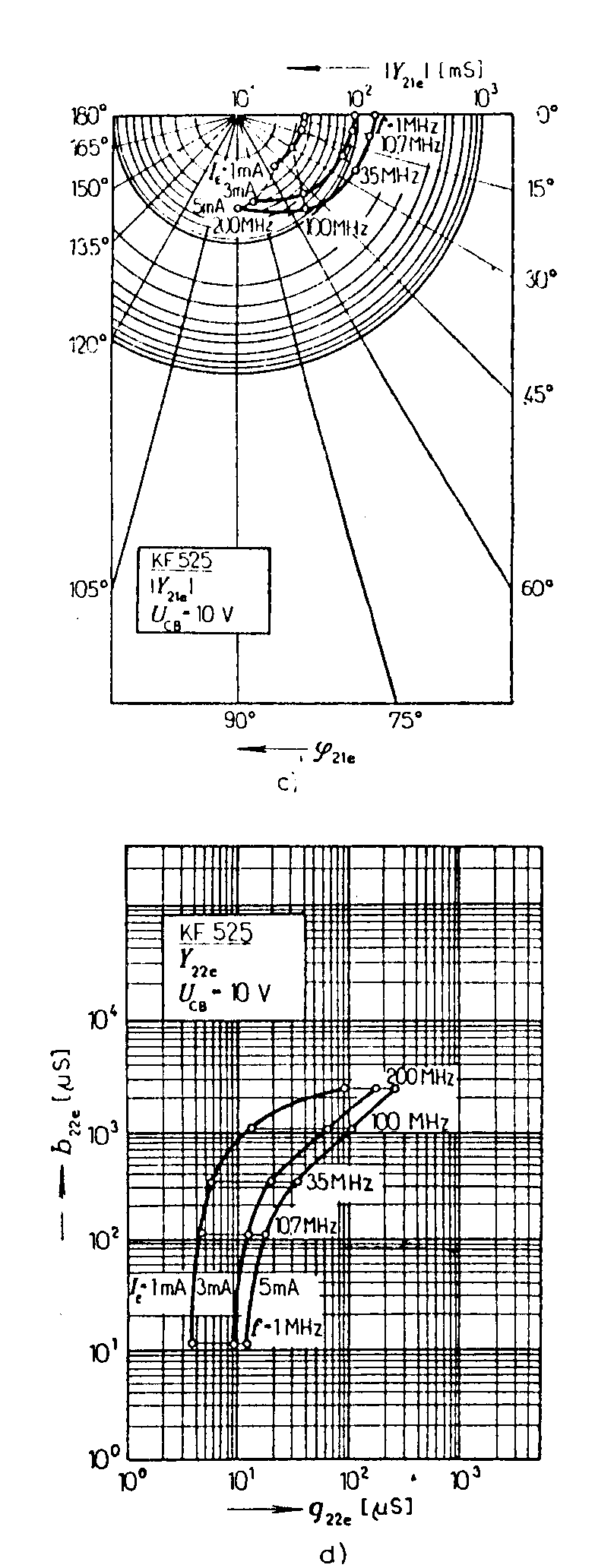
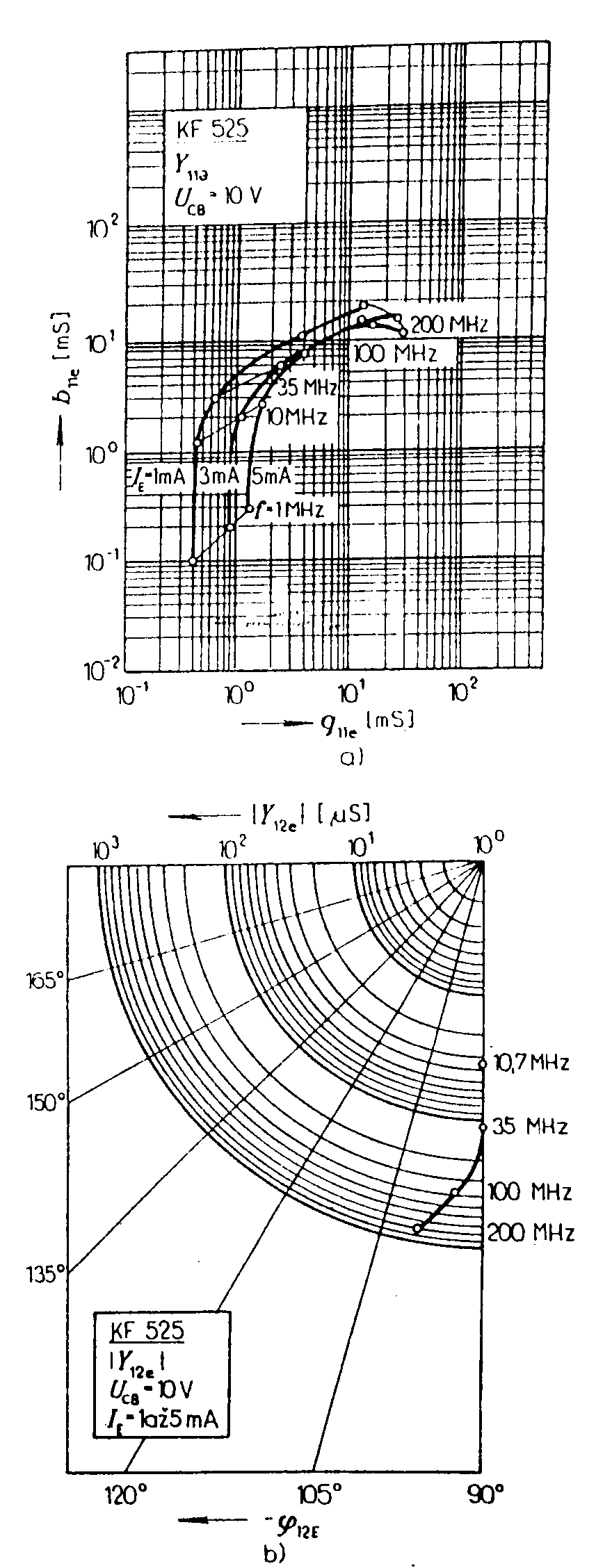
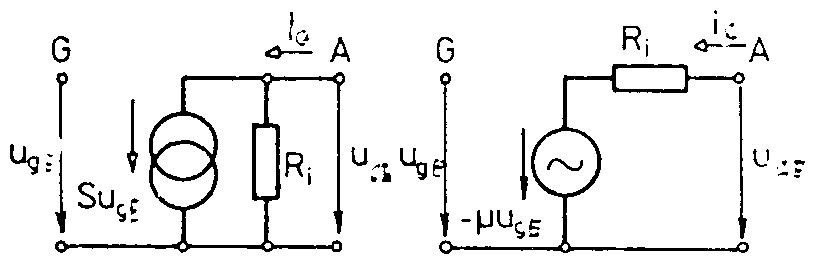
Tranzistor jako čtyřpól. Díváme-li se na tranzistor jako na čtyřpól, lze jeho vlastnosti vyjádřit pomocí čtyřpólových rovnic.Ve většině případů jsou udávány parametry tranzistoru ve tvaru t.zv. h-parametrů, neboli smíšených parametrů. Soustava těchto rovnic má tvar: Význam parametrů h má následující význam: při výstupu nakrátko. naprázdno. výstupu nakrátko. při vstupu naprázdno. Parametry hij jsou tedy střídavé parametry, určované v okolí pracovního bodu. Při vysokých frekvencích nelze dobře dodržet definiční podmínky jednotlivých parametrů, protože měřící generátory i voltmetry mají vždy určitou kapacitu, která vstup nebo výstup zkratovává a není splněna podmínka vstupu naprázdno. Proto udává výrobce u vf tranzistorů parametry admitanční, které jsou definovány následovně: Význam parametrů y je následující: výstupu nakrátko. při vstupu nakrátko. při výstupu nakrátko. Je vidět, že všechny definiční podmínky parametrů vyžadují vstup nebo výstup nakrátko, což se snadno realizuje pomocí kondenzátorů. Tyto vf parametry udává výrobce obyčejně v grafech a to buď v polárních nebo v pravoúhlých souřadnicích. Příklad parametrů pro vf tranzistor KF 525 je uveden na obr. na str.12. Mezi h-parametry a y-parametry existuje jednoznačné vztahy, které jsou uvedeny v tabulce.
Tranzistorové zesilovače mohou pracovat ve třech možných zapojeních. V zapojení se společným emitorem, společným kolektorem nebo se společnou bází. V katalozích bývají uváděny pouze parametry pro zapojení se společným emitorem. Pro ostatní dvě zapojení se parametry přepočítají podle následující tabulky:
Ze známých h-parametrů lze vypočítat parametry zesilovače AU,Ai,r1,r2.
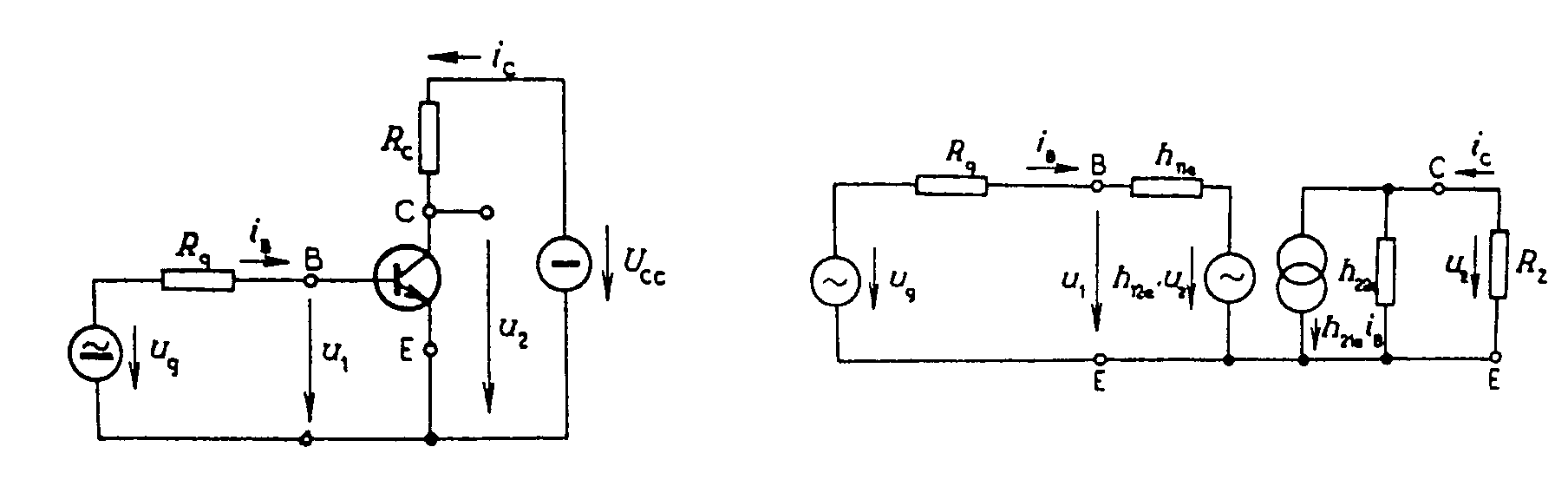
Admitanční parametry tranzistoru KF525 Zesilovací stupně s bipolárními tranzistory. 1) Tranzistorový stupeň se společným emitorem. Společnou elektrodou vstupního a výstupního obvodu je emitor. Schema zapojení je na obr. Napěťový přenos Řešením rovnic dostaneme Pro RZ = 0 je pro RZ ® ¥
je V praxi velmi často platí, že RZ
«
Průběh přenosu je na obr. Proudový přenos je definován vztahem Dostaneme Minimální proudový přenos je při Výkonový přenos je definován Pro Pro malé odpory RZ je Při velkých RZ je Výkon se zvětšuje s druhou mocninou parametru h21e. Vstupní odpor je dán vztahem Řešením těchto rovnic dostaneme Pro Výstupní odpor je definován vztahem
Řešením rovnic dostaneme vztah Uvedený vztah nezahrnuje kolektorový odpor RC.
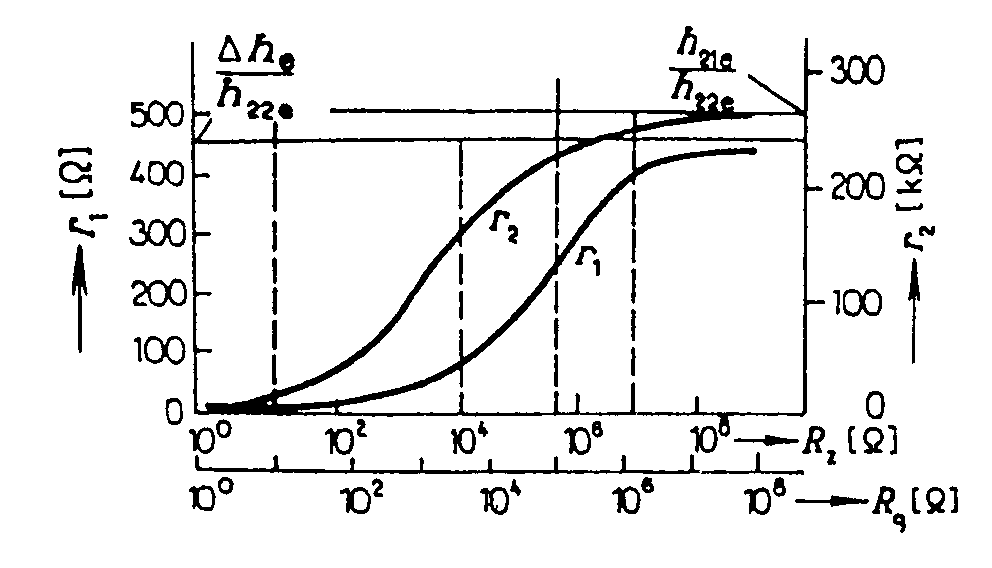
Skutečný výstupní odpor je Tento odpor je nutno rozlišovat od skutečného zatěžovacího odporu RZ. Odpor RC je odpor v kolektoru řešeného stupně a odpor RZ je zatěžovací odpor řešeného stupně a paralelně vstupní odpor následujícího stupně. Vstupní kapacita stupně v zapojení SE je dána vztahem kde CBE je kapacita báze - emitor tranzistoru CBC je průchozí kapacita tranzistoru. Tento druhý člen má rozhodující vliv u stupňů s velkým zesílením. Výstupní kapacita se určí ze vztahu Jen v případě proudového buzení je h11e « Rg a potom má druhý člen tvar h21e.CBC. 2) Tranzistorový zesilovací stupeň se společným kolektorem - SC. V katalogu udává výrobce pro tranzistory pouze v zapojení SE. Používáme-li tranzistor v zapojení SC nebo SB, přepočteme parametry pro zapojení SE na parametry pro zapojení SC (SB) a tyto parametry dosazujeme do vzorců pro AU, Ai, Ap, r1, r2. Převodní vztahy pro přepočet parametrů jsou uvedeny na str. 13. Schéma zapojení zesilovacího stupně v zapojení SC je na obr. Dosazením přepočtěných vztahů do vzorců pro AU dostaneme: pro Proudový přenos Ai je největší při -(1+h21e) a RZ < 1/h22e. S rostoucím RZ proudový zesilovací činitel klesá. Výkonové zesílení Ap má největší hodnotu číselně rovnou parametru h21e. Závislost vstupního odporu na zatěžovacím odporu a výstupního odporu na odporu Rg je uvedena na obr. Výstupní impedance unipolárního zesilovač v zapojení SC. Zapojení zesilovače a jeho náhradní schéma je na obr. Pro určení výstupní impedance odpojíme zátěž a předpokládáme, že na výstupních svorkách je připojen externí zdroj o napětí u2, který protlačuje do zesilovače proud i. Velikost proudu je Výstupní impedance mezi emitorem a je společnou svorkou je Zatěžovací impedance Rz = RE je připojena k impedanci r2 paralelně. Vstupní impedance. Předpokládejme zapojení podle obr. Do vstupu teče proud Odtud vstupní odpor Vstupní odpor tranzistoru je v tomto zapojení o tři řády větší, než odpor h11e a je ovlivňován hlavně proudovým zesilovacím činitelem. Výstupní odpor je pro Rg = 0 roven h11e/h21e a pro Rg ® ¥ je 1/h22e. Tento stupeň se také nazývá emitorový sledovač, protože emitorové napětí sleduje fázi vstupního napětí. Napěťový přenos je vždy < 1. Vstupní odpor je tím větší a výstupní tím menší, čím je větší h21e. 3) Tranzistorový stupeň se společnou bází - SB. Schema zapojení je na obr. Teoreticky se hodnota napěťového přenosu liší málo
od zapojení SE, pouze zde není fázový posuv mezi vstupním a výstupním napětím.
Pro Rz®¥ je napěťový přenos
přibližně h21e/Dhe a pro Rz =
0 je napěťový přenos roven 0. Závislost napěťového zesílení AU na
Rz je na obr. Proudové přenosy pro Rz = 0 jsou Vstupní odpor má pro Rz = 0 hodnotu h11e/h21e a pro Rz ® ¥ je Dhe/h22e. Při zatěžovacích odporech do 104 W je vstupní odpor malý (desítky ohmů). Při větších odporech Rz je stovky ohmů. Výstupní odpor se pohybuje v hodnotách jednotek až stovek ohmů. Závislosti odporů jsou rovněž na obrázku. Shrnutí vlastností jednotlivých zapojení. Zapojeni SE. Výkonové zesílení je největší ze všech sledovaných zapojení, ale je velmi závislé na parametru h21e. Napěťové zesílení se pohybuje ve stovkách, ale zapojení otáčí fázi napětí. Proudové zesílení je rovněž velké, výstupní proud je ve fázi se vstupním. Vstupní odpor je řádově jednotky kilohmů, výstupní odpor jsou desítky kilohmů.
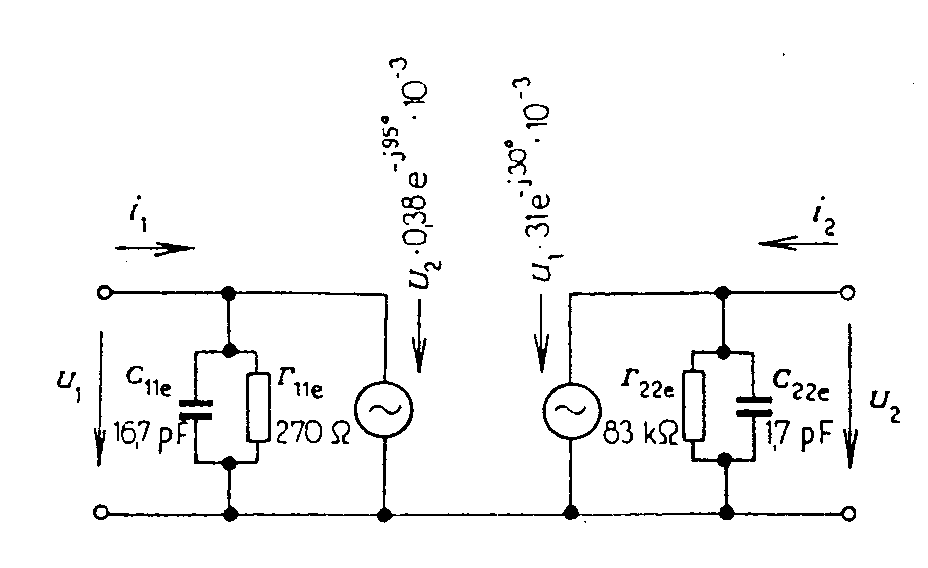
Zapojení SC. Napěťové zesílení je vždy menší než jedna, výstupní napětí je ve fázi s napětím vstupním. Proudové zesílení je velké, výstupní proud je v protifázi oproti vstupnímu. Vstupní odpor je velký (o několik řádů větší, než u zapojení SE), výstupní odpor je malý. Zapojení se používá buď k snímání signálu ze zdrojů s velkým vnitřním odporem (např. krystalové přenosky) nebo k přizpůsobení výstupu zesilovače na malý zatěžovací odpor (např. na koaxiální kabel). Zapojení SB. Napěťové zesílení je velké (jako u zapojení SE), výstupní signál je ale ve fázi se vstupním. Proudové zesílení je vždy menší než jedna. Vstupní odpor je malý (jednotky až desítky ohmů), výstupní odpor je velký (stovky kilohmů až jednotky megohmů). Zapojení se používá k snímání signálů zdrojů s malým vnitřním odporem (antény, termočlánky). Příklad: Pro tranzistor KF 508, který má v pracovním bodě UCE =5V a IC =1mA parametry h11e = 2,4 kW, h12e = 7,3.10-4, h21e = 150, h22e = 2,4.10-5 mS určete pro Rg = 10 kW a Rz = 10 kW hodnoty Ai, AU, r1 a r2 pro všechna zapojení SE, SC, SB. 1) zapojení SE: 2) Pro zapojení SB, přepočítáme parametry he na parametry hB. Dosazením do výše uvedených vzorců vypočítáme: 3) Pro zapojení SC přepočítáme parametry he na parametry hC: h11C = h11e = 2,4 kW h12C = 1 - h12e = 1 - 7,3.10-4 = 0,999 h21C = -(1+h21e) = -(1+150) = -151 h22C = h22e = 2,4.10-5 S DhC = h11C.h22C - h12C.h21C = 2,4.103.2,4.10-5 - 0,999.(-151)=150,9 Opět dosazením do výše uvedených vzorců dostaneme: Na uvedeném příkladě jsou jasně vidět závěry, které byly učiněny v souhrnu jednotlivých zapojení. Pro vysokofrekvenční tranzistory udává výrobce z výše uvedených důvodů y - parametry. Pro ilustraci uvedeme příklad výpočtu pro tranzistor typu KF 525. Parametry tranzistory jsou uvedeny na str. 12. Příklad: Pro tranzistor KF 525 určit v pracovním bodě UCB = 10 V, IE = 1mA na frekvenci f = 100 MHz y - parametry pro zapojení SE, SB a SC a vstupní impedanci pro zapojení SE, je-li zatěžovací impedance Yv = (1 - j). 10-3 S a výstupní impedanci v zapojení SB, je-li Yg = (0,012 + j1,05).10-3 S. Řešení. Z charakteristik pro SE se určí: Všechny parametry vyjádříme v obou tvarech (polárním i kartézském). Hodnoty ekvivalentních kapacit z vstupních a výstupních admitanèních parametrù : Je tedy hodnota vstupní kapacity s uzemněným emitorem a hodnota výstupní kapacity s uzemněným emitorem Přepočet parametrů y na zapojení SB: Přepočet parametrů y pro zapojení SE na zapojení SC: Vstupní a výstupní odpor v zapojení SE: Náhradní schéma tranzistoru v zapojení SE v pracovním bodě UCB = 10 V, IE = 1mA a f = 100 MHz: Zapojíme-li tranzistor jako zesilovač, v zapojení SE se zatěžovací impedancí Yz, , je vstupní impedance zesilovacího stupně:
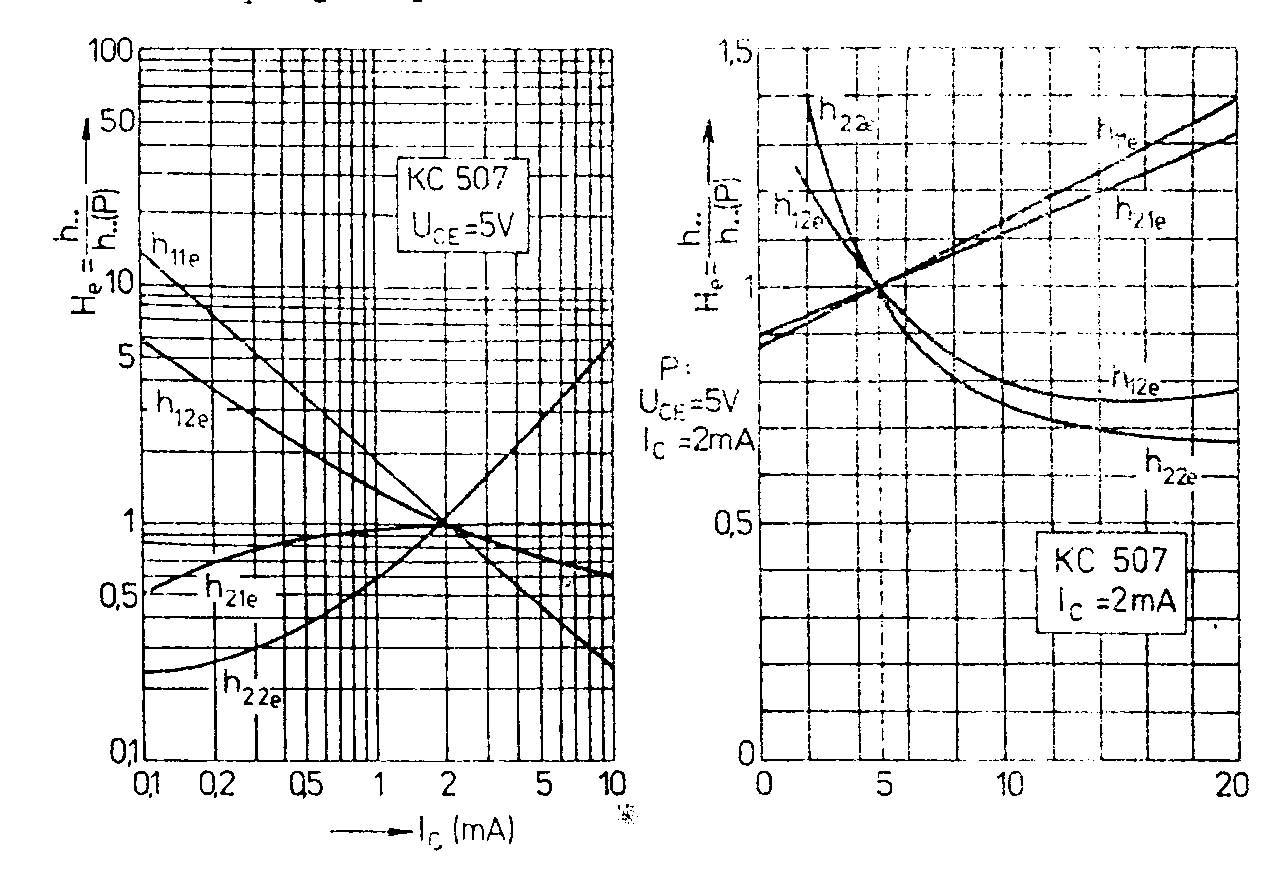
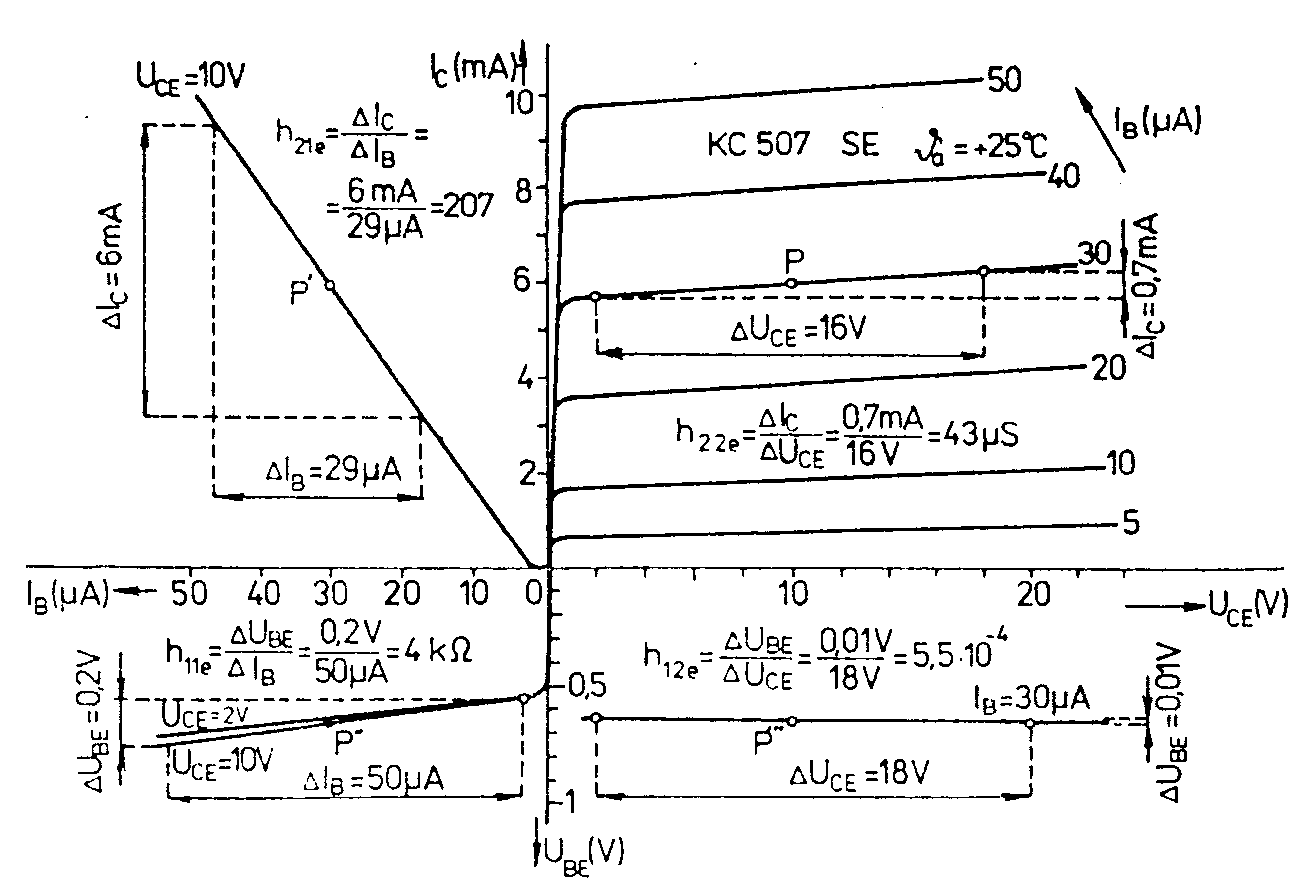
= Zapojíme-li tranzistor jako zesilovací stupeň v zapojení SB se vstupní impedancí YG, je výstupní impedance tohoto stupně: = Čtyřpólové parametry tranzistoru jsou závislé na pracovním bodě. Proto bývají v katalozích jejich hodnoty udávány pro definovaný pracovní bod. Je-li pracovní bod tranzistoru jiný, udává výrobce převodní grafy, z nichž se odečtou koeficienty, kterými se v závislosti na jiný kolektorový proud nebo jiné napětí kolektor-emitor vynásobí udané čtyřpólové parametry. Jako příklad jsou na obr. uvedeny grafy pro převod parametrů tranzistoru KC507 pro jiné hodnoty výstupních veličin. Čtyřpólové parametry lze rovněž odečíst z charakteristik tranzistoru. Na obr. jsou uvedeny charakteristiky tranzistoru KC507. V prvním kvadrantu jsou uvedeny výstupní charakteristiky. Z nich lze odečíst parametr h22e. Ve druhém kvadrantu je uvedena převodní charakteristika. Z ní lze odečíst v pracovním bodě parametr h21e. Ve třetím kvadrantu jsou uvedeny vstupní charakteristiky a v pracovním bodě lze odečíst parametr h11e. Ve čtvrtém kvadrantu je uvedena zpětná charakteristika a v pracovním bodě lze odečíst parametr h12e. Závislost h-parametrů na frekvenci. Při nízkých frekvencích jsou h-parametry pouze reálná čísla. Při vyšších frekvencích, když jsou doby průchodu signálu přes přechody srovnatelné s periodou zpracovávaných signálů, jsou ovšem h-parametry komplexní čísla. Např.pro proudový zesilovací činitel platí vztah Kromě mezní frekvence se společným emitorem fm
= fh21e je uvedena tranzitní frekvence tranzistoru fT.
Je to frekvence, při níž klesne parametr h21e na hodnotu 1. Tato
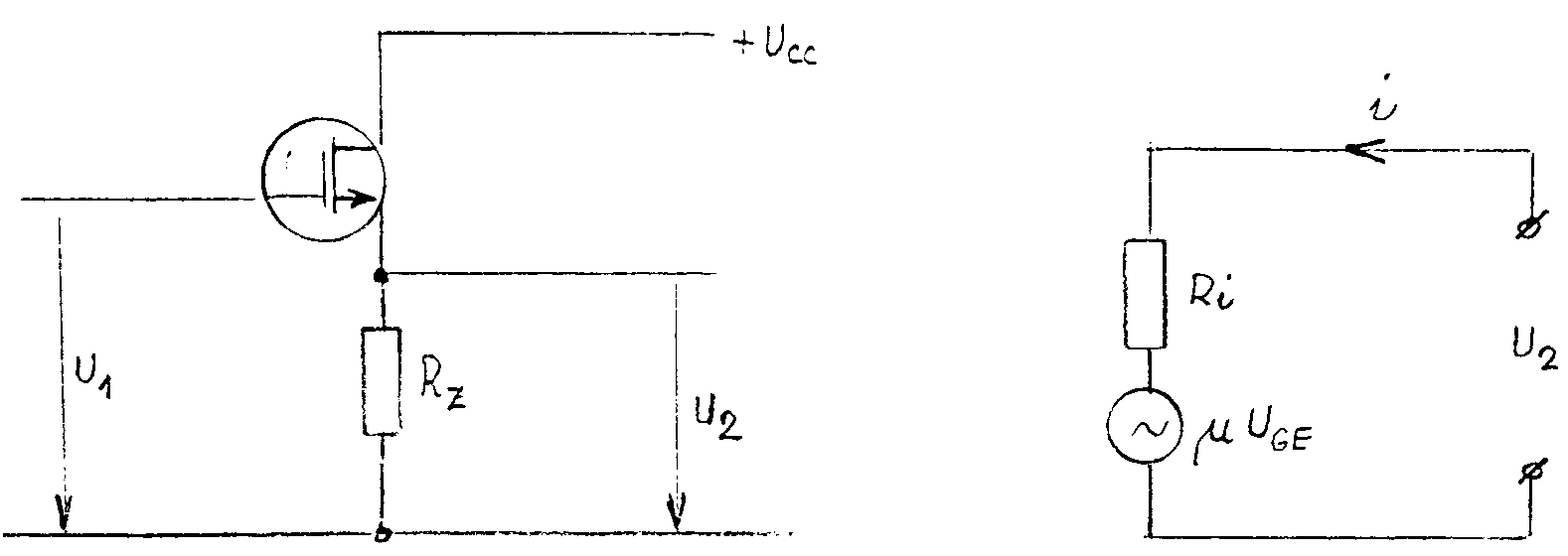
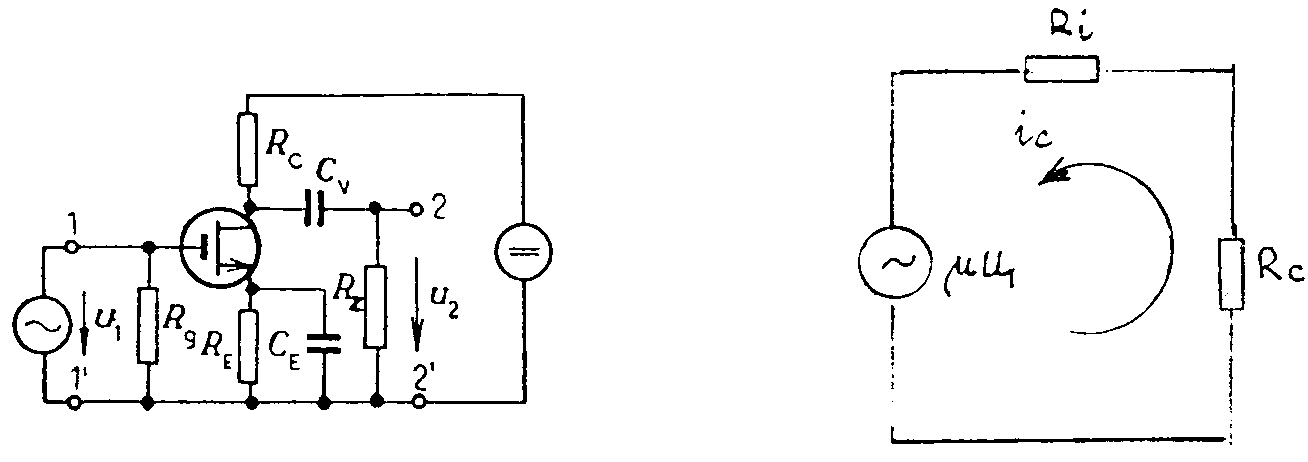
se jen málo liší od frekvence fh21b. Platí Zesilovací stupně s unipolárními tranzistory. Napíšeme-li čtyřpólové rovnice pro unipolární tranzistor ve tvaru pro y-parametry, odpadá první rovnice, protože vstupní proud i1 = 0 a vstupní vodivost y11 je rovněž nula. Zůstává pouze druhá rovnice U unipolárních tranzistorů (stejně jako u elektronek) se zavádí pojmy: Mezi těmito vztahy platí t.zv. Barkhauzenův vztah S.Ri = m. Pomocí těchto veličin lze nakreslit nahradní schema unipolárního tranzistoru. Tranzistor nahradíme mezi kolektorem a emitorem buď zdrojem konstantního napětí mUGE v serii s vnitřním odporem Ri, nebo zdrojem konstantního proudu SUGE s paralelně připojeným odporem Ri (viz obr.) Zesilovací stupeň s unipolárním tranzistorem v zapojení SE. Schéma zapojení je na obr. Z náhradního schematu lze napsat rovnici: Výstupní odpor r2 = Ri. Vstupní odpor je velmi vysoký, je dán typem tranzistoru a bývá 1011 - 1013W. Protože není přesně definován, zapojuje se na vstupu odpor R1, který potom vstupní odpor přesně definuje. Volí se obvykle 1010W, abychom neztratily celkový požadovaný vysoký vstupní odpor. Pro Rc « Ri je AU = -SRc,
pro Rc ® ¥ je AU = -m
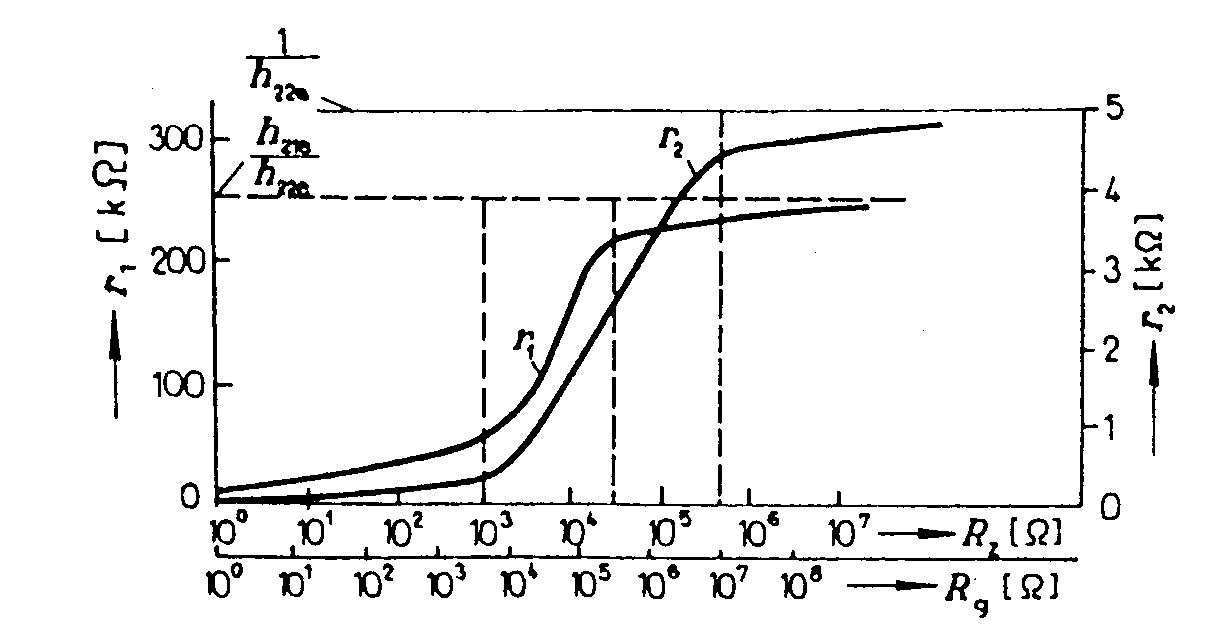
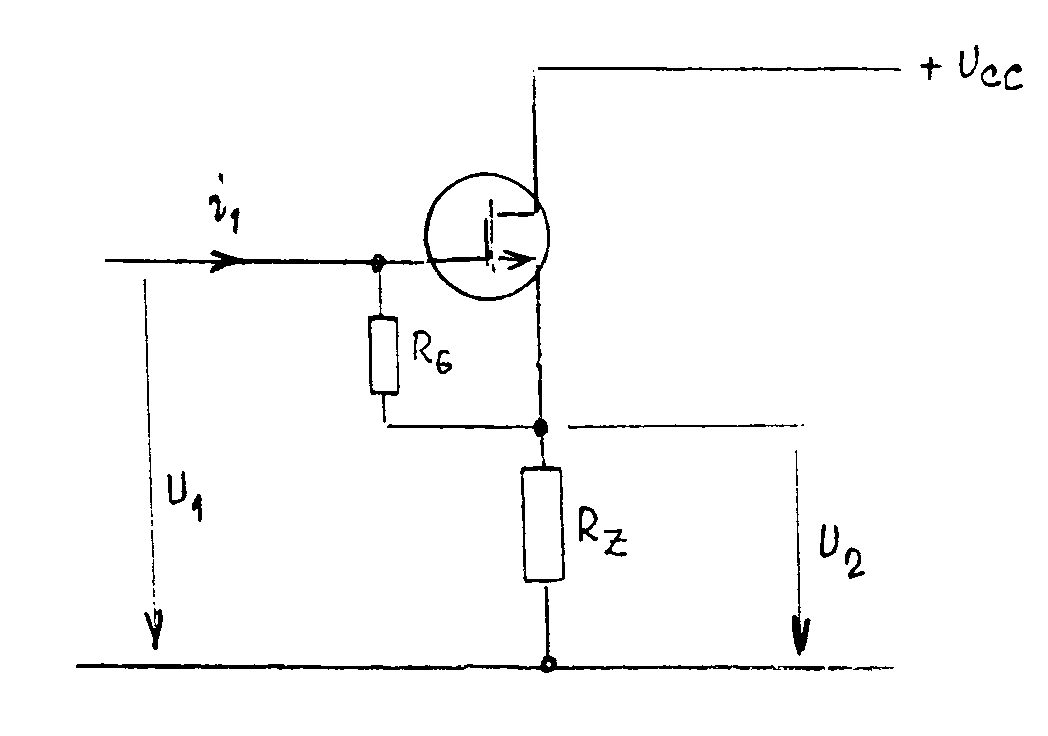
= Zesilovací stupeň s unipolárním tranzistorem v zapojení SC. Schéma zapojení je na obr. Řídící napětí je dáno rozdílem (u1 - u2).Z náhradního schematu lze napsat rovnici: Pro Rz = 0, je AU = 0. Pro
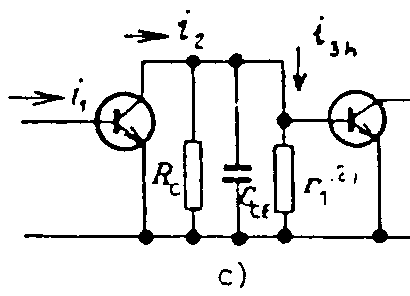
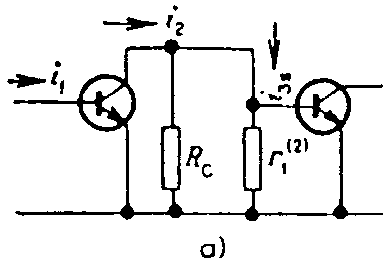
Rz ® ¥ je Pro vstupní odpor lze odvodit vztah Výstupní odpor je dán vztahem Zesilovací stupeň s unipolárním tranzistorem v zapojení SG. Schéma zapojení je na obr. Z náhradního schematu lze napsat rovnici: Pro vstupní odpor lze odvodit vztah Výstupní odpor je dán vztahem Vícestupňové zesilovače. Předpokládáme zapojení stupňů SE. Zapojení SE je nejvýhodnější, protože jednotlivé stupně mají relativně nejmenší rozdíly mezi vstupními a výstupními impedancemi a největší výkonové zesílení. Průběh kmitočtové charakteristiky v oblasti nízkých kmitočtů závisí na velikosti vazebních kapacit Cv, v oblasti středních kmitočtů je dáno zesílení pouze odpory Rc a stabilizační odpory ve vstupních obvodech. V oblasti vysokých kmitočtů závisí zesílení hlavně na vlastnostech tranzistorů a na parazitních kapacitách v jednotlivých stupních. Celkové zesílení je dáno součinem zesílení jednotlivých stupňů (nebo součtem zesílení jednotlivých stupňů v decibelech). Každý článek, obsahující kmitočtově závislý člen
zvětšuje strmost charakteristiky o 6 dB/okt, takže celkový horní mezní kmitočet
fhc se snižuje proti kmitočtu fh jednotlivých stupňů.
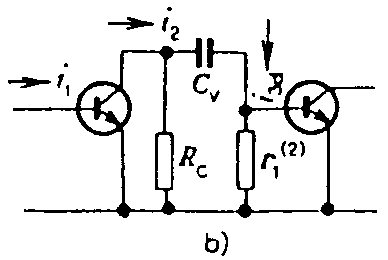
Pro n stejných stupňů platí Podobné závěry lze udělat i v oblasti dolního mezního kmitočtu. Přenos středních kmitočtů. Na obr. je náhradní schéma pro přenos středních kmitočtů. Výsledný odpor Rp je paralelní kombinace odporů R1 a R2. Obyčejně ho můžeme zanedbat vzhledem ke kolektorovému odporu Rc. Zatěžovací odpor je dán paralelní kombinací kolektorového odporu Rc a vstupního odporu druhého stupně r1(2). Tranzistor druhého stupně je buzen proudem, který se vypočítá z rovnice odtud proud is3 za proud i2 lze dosadit vztah Proudové zesílení tranzistorového zesilovače v oblasti středních kmitočtů Hodnota tohoto zesílení není závislá na kmitočtu a je určena pouze výrazem, uvedeným ve zlomku dané rovnice. Přenos nízkých kmitočtů. Náhradní schéma pro přenos nízkých kmitočtů je na obrázku. Při nízkých kmitočtech se uplatňují reaktance vazebních kondenzátorů Cv. S klesajícím kmitočtem roste jejich reaktance a klesá budící proud druhého stupně. Pro dělič proudu platí Za i2 lze opět dosadit, takže dostaneme Proudové zesílení v oblasti nízkých kmitočtů je tedy Absolutní hodnota poměrného zesílení v oblasti nízkých kmitočtů je dána Pro dolní mezní kmitočet, při kterém dochází k poklesu
zesílení o 3 dB platí, Rovněž emitorový odpor působí pokles zesílení v oblasti
nízkých kmitočtů. Blokovací kondenzátor CE začne při nízkých kmitočtech
zvyšovat svojí reaktanci, emitorový odpor RE začne zavádět zápornou
zpětnou vazbu a nastává pokles zesílení. Pro určení hodnoty emitorového kondenzátoru
se neuvažuje vazební kondenzátor Cv a používá se přibližný vztah
Kondenzátor CE způsobí na dolní mezní
frekvenci pokles zesílení stejně jako Cv na hodnotu Příklad. Uvažujme tranzistor s mezním kmitočtem fh21b = 1 MHz, Ccb = 40 pF, h21e = 50. Mezní kmitočet pro zapojení SE je Požadujme horní mezní kmitočet dvoustupňového zesilovače 10 kHz. Na tomto kmitočtu bude tedy pokles zesílení a stupeň U dvou stupňů bude tedy pokles zesílení 2.0,97 = 1,94 dB. Na vliv kapacity tedy zbývá na jeden stupeň (3-1,94):2=0,53 dB. Lze tedy psát Přenos vysokých kmitočtů. Náhradní schéma pro přenos vysokých kmitočtů je na obr. Platí rovnice dosadíme-li opět za i2, dostaneme zesílení při vysokých kmitočtech pokles zesílení o 3 dB vzhledem ke středním kmitočtům je při Při kapacitě Cce = 2000 pF a horní mezní frekvenci f = 29,5 kHz, je největší přípustný odpor Literatura : Maťátko, Elektronika, SNTL, Boltík a kol., Elektronická zařízení, SNTL, Hojka a kol., Radioelektronická zařízení I., SNTL, Vackář a j., Radioelektronická zařízení, SNTL |
|
zpět na předchozí stránku
Copyright © 2003 Hell
doporučené rozlišení 1024x768

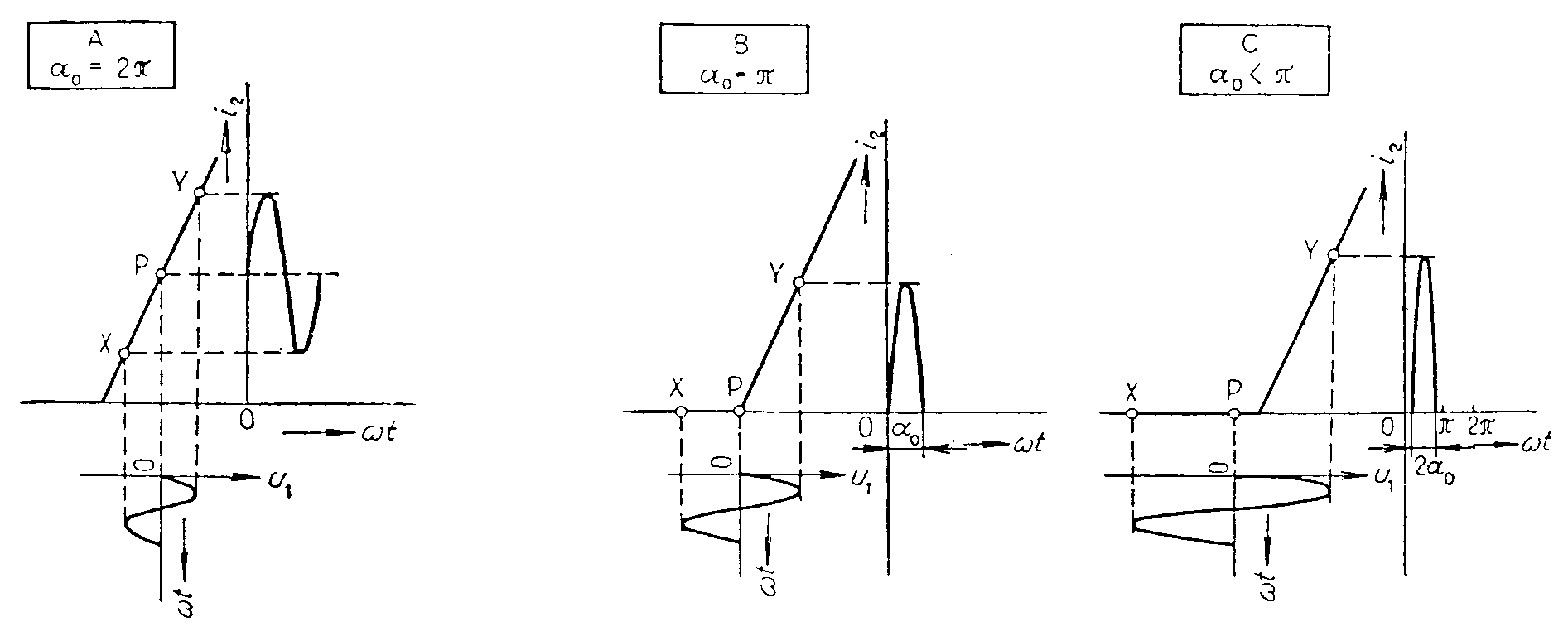
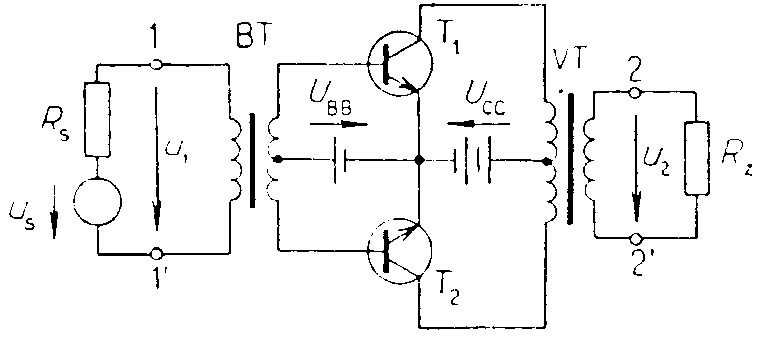
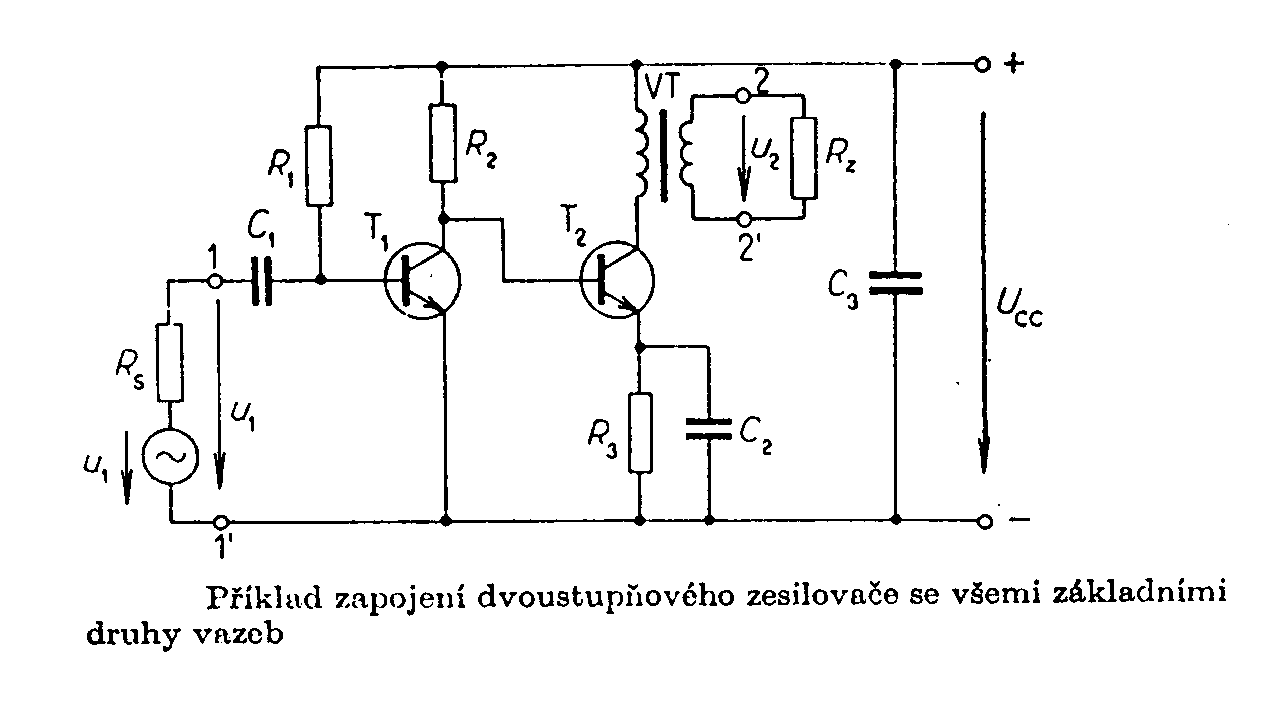
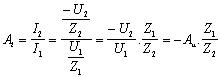 , kde Z1
je vstupní impedance a Z2 je výstupní impedance.
, kde Z1
je vstupní impedance a Z2 je výstupní impedance.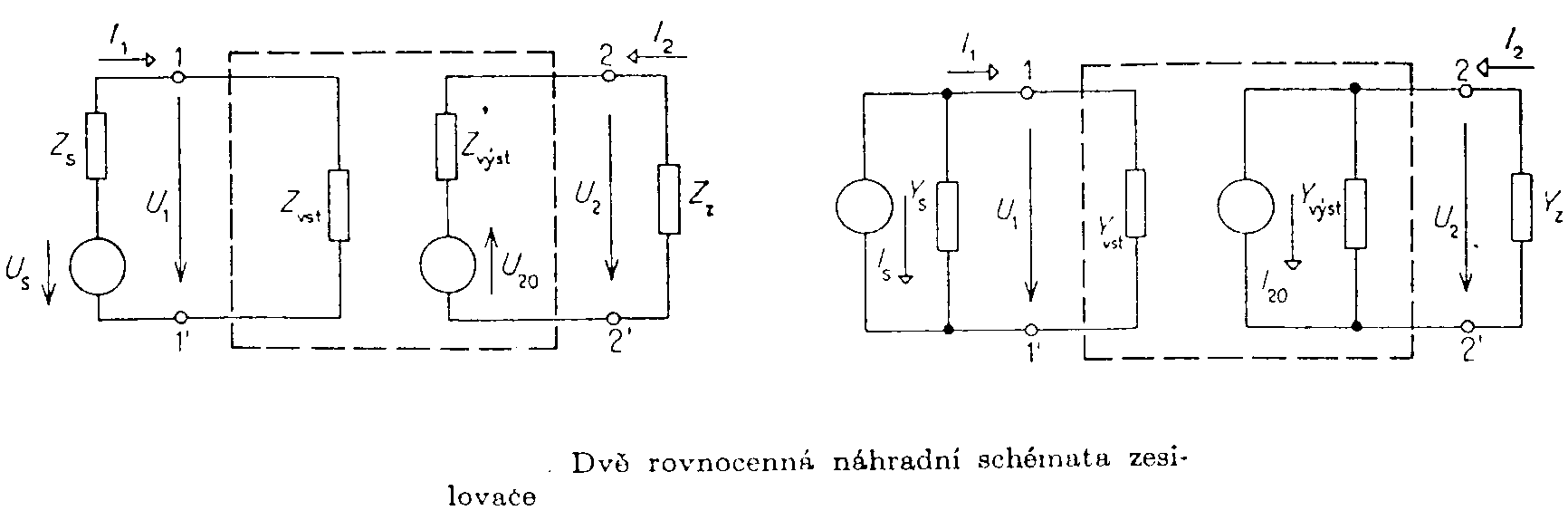
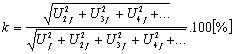
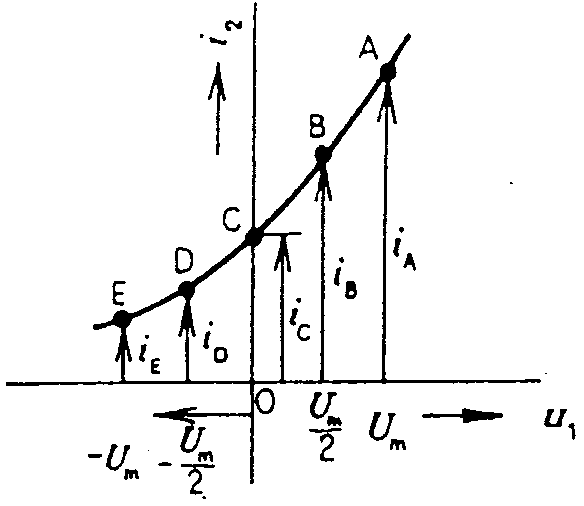

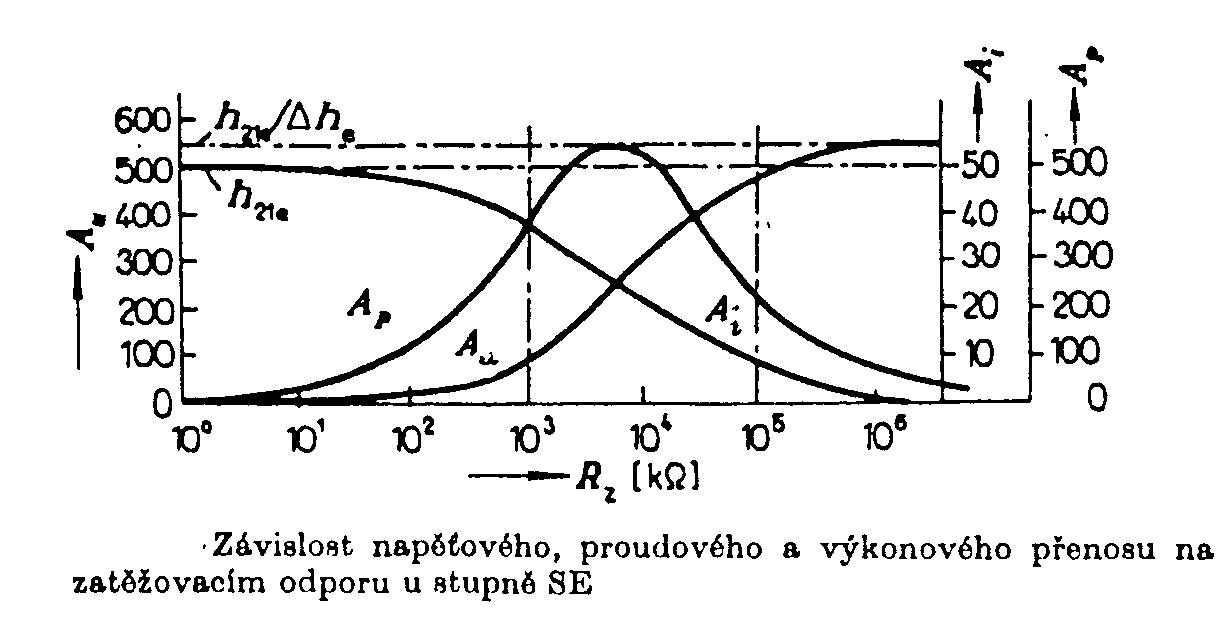

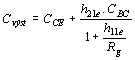 . Obyčejně
bývá h11e
. Obyčejně
bývá h11e 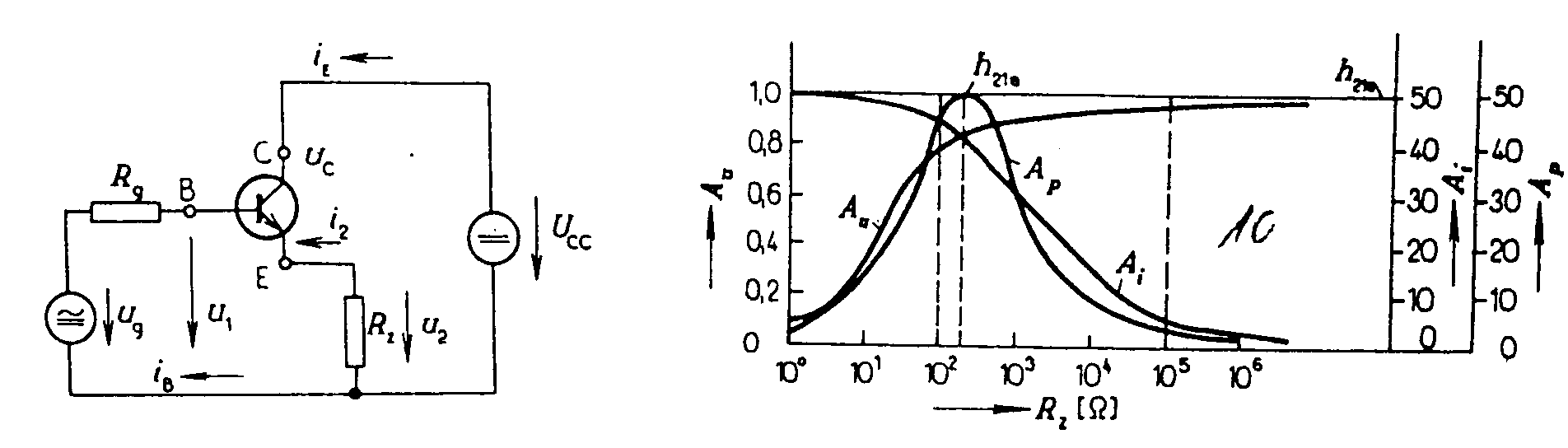
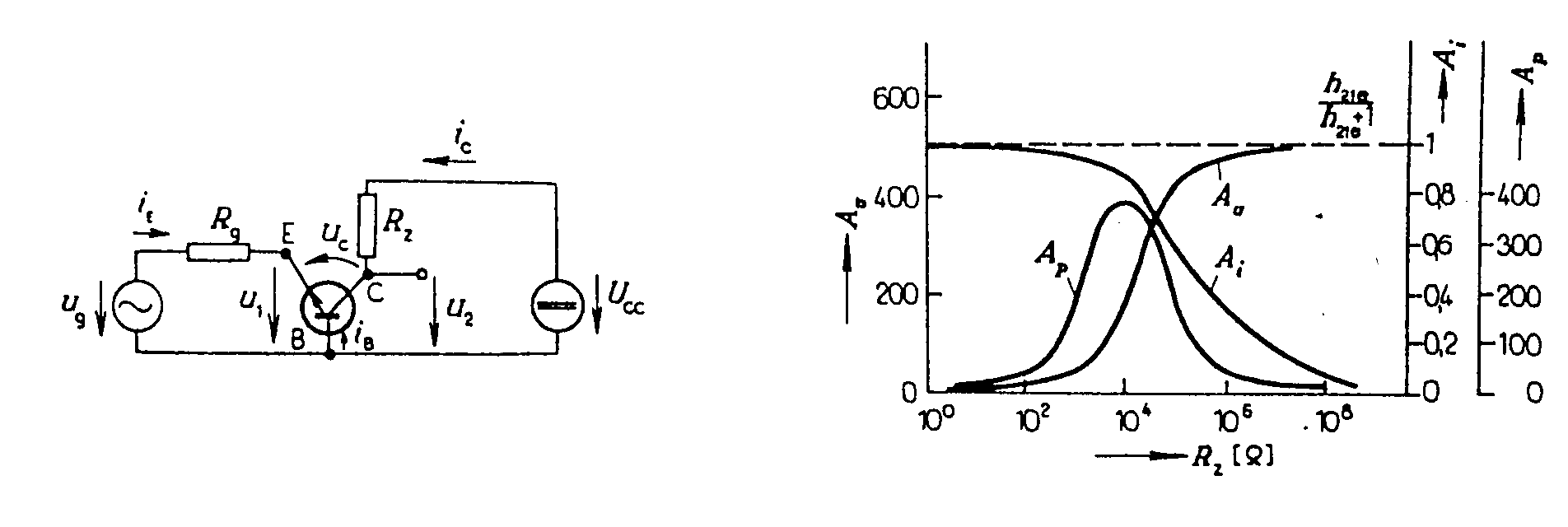
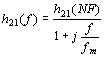 , kde fm
je mezní frekvence, při které klesá absolutní hodnota proudového činitele
, kde fm
je mezní frekvence, při které klesá absolutní hodnota proudového činitele
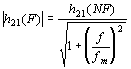 o 3 dB. Závislost
je uvedena na obr.
o 3 dB. Závislost
je uvedena na obr.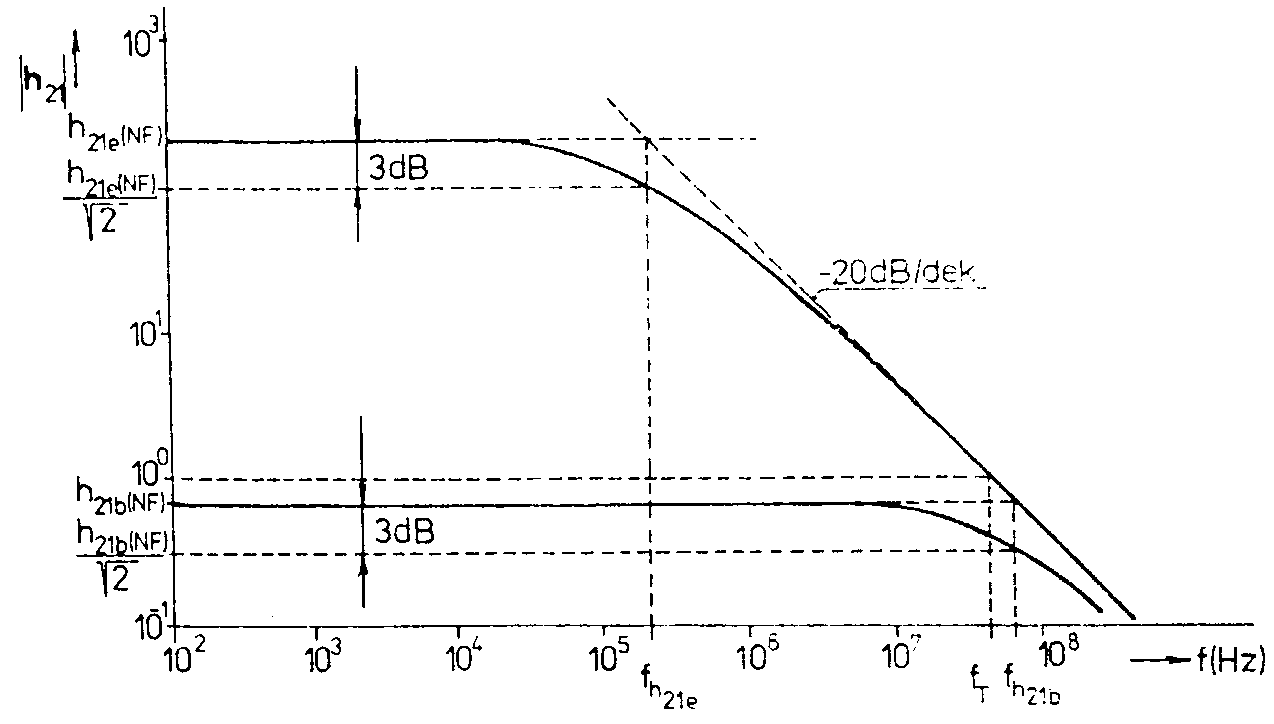
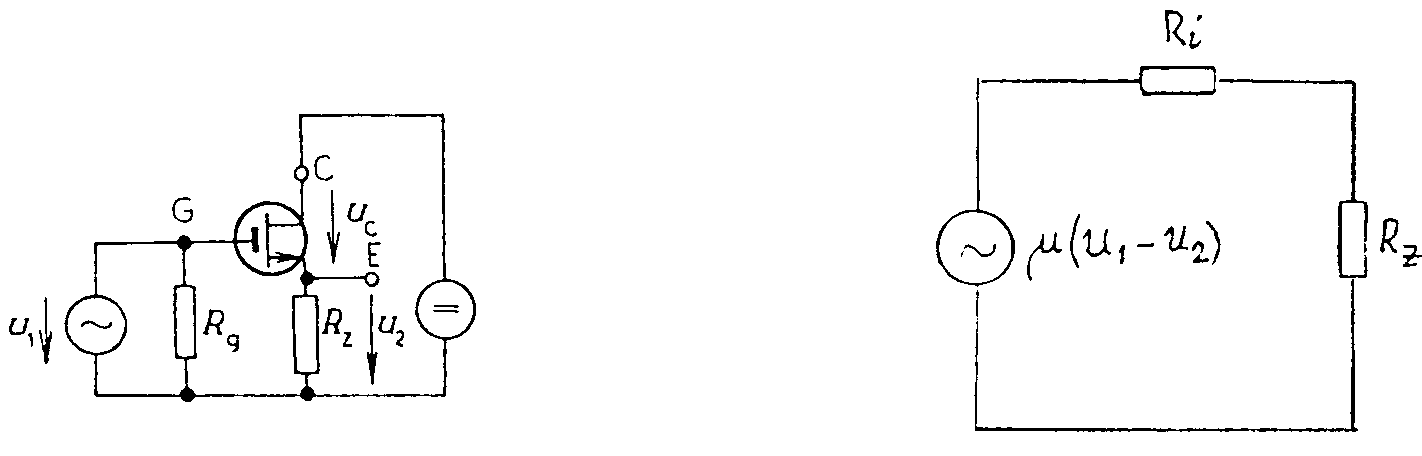
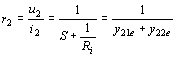 .
.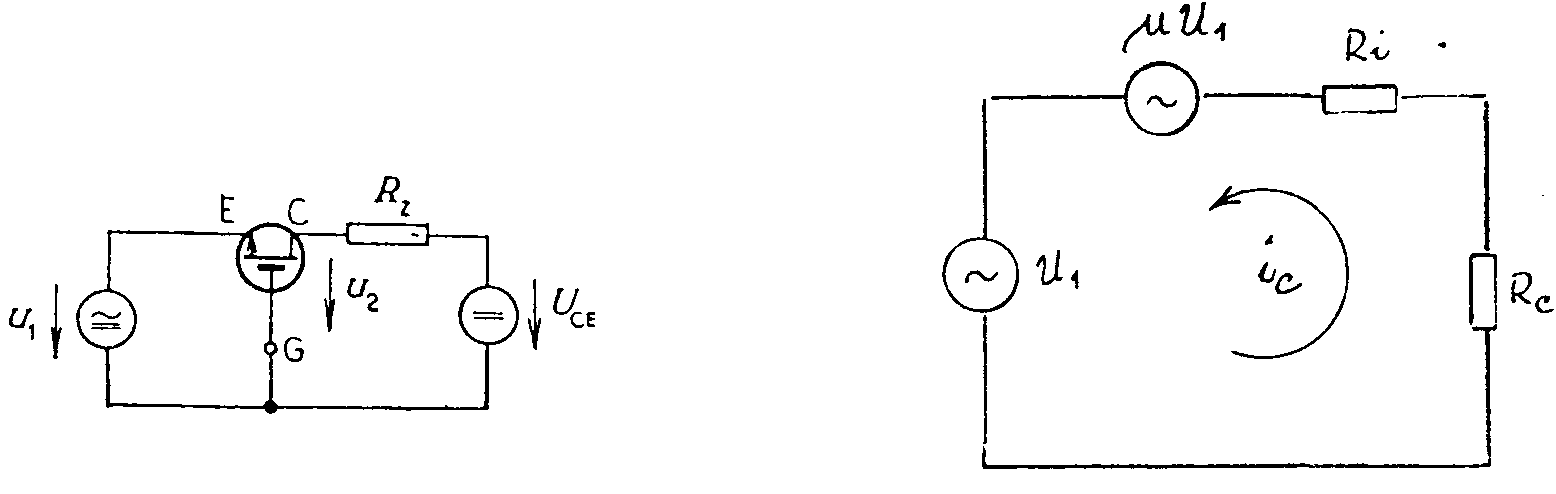
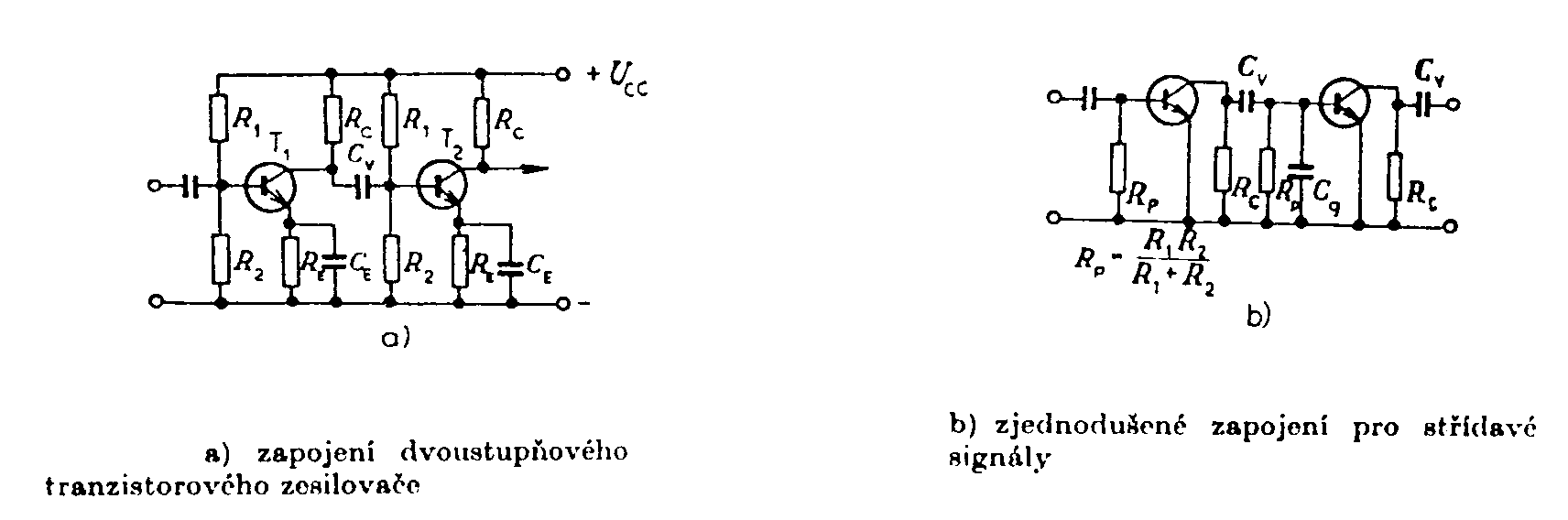
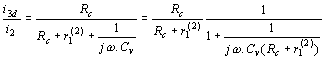
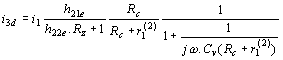
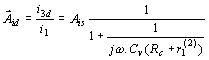
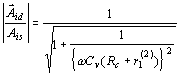
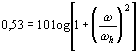 . Odtud
. Odtud